
- •Учебное пособие
- •Содержание
- •1. Физические основы механики
- •1.1. Основные формулы
- •1.2. Примеры решения задач к разделу «Механика»
- •1.3. Базовые задачи для самостоятельного решения
- •1.4. Контрольные вопросы
- •2. Основы молекулярной физики и термодинамики
- •2.1. Основные формулы
- •2.2. Примеры решения задач к разделу «Молекулярная физика и термодинамика»
- •2.3. Базовые задачи для самостоятельного решения
- •2.4. Контрольные вопросы
- •Библиографический список
- •Приложения
- •1. Основные физические постоянные (округленные значения)
- •2. Некоторые астрономические величины
1.1. Основные формулы
Средняя скорость
и среднее ускорение:
![]() ;
;![]() .
.![]()
где S– путь, пройденный точкой за интервал времениt.
Путь Sв отличие от разности координатx = x2 – x1не может убывать и принимать отрицательные значения, т.е.S0.
Величина мгновенной скорости и мгновенного ускорения при прямолинейном движении соответственно:
![]() или
или
![]() ;
;![]()
Тангенциальная и нормальная составляющая ускорения при криволинейном движении:
![]() ;
;
![]() ,
гдеR– радиус кривизны траектории.
,
гдеR– радиус кривизны траектории.
Полное ускорение
![]() ;
;![]()
Кинематическое уравнение равнопеременного движения материальной точки (центра масс твердого тела) вдоль оси X:
![]() ,
,
где хо– начальная координата движущейся точки в момент времениt= 0;
![]() o– скорость точки в данный момент
времени;
o– скорость точки в данный момент
времени;
а – мгновенное ускорение.
Скорость и путь равнопеременного поступательного движения:
 .
.
Угловая скорость и угловое ускорение при вращательном движении:
![]() ;
;
![]() .
.
Кинематические уравнения равнопеременного вращательного движения:

Связь между линейными и угловыми величинами при вращательном движении: длина дуги, пройденная точкой:
![]() ,
,
где – угол поворота точки,R– радиус вращения точки;
![]() ;
;
![]() ;
;![]() .
.
Импульс (количество
движения) материальной точки массой m,
движущейся со скоростью![]() :
:
![]() .
.
Основное уравнение динамики поступательного движения:
![]() .
.
Силы, рассматриваемые в механике:
а) сила упругости:
![]() ,
,
где k– коэффициент упругости;
x– абсолютная деформация;
б) сила трения скольжения:
![]() ,
,
где f– коэффициент трения;
N– сила нормального давления;
в) сила гравитационного взаимодействия (сила тяготения):
![]() ,
,
где G – гравитационная постоянная;
m1иm2– массы взаимодействующих тел;
r– расстояние между телами (тела рассматриваются как материальные точки);
г) сила, действующая на тело, движущееся по дуге окружности радиуса R:
![]() .
.
Закон сохранения импульса (количества движения) для замкнутой (изолированной) системы:
![]() ,
,
или для двух тел (i= 2):
![]() ,
,
где
![]() и
и![]() – скорости тел в начальный момент
времени (до взаимодействия);
– скорости тел в начальный момент
времени (до взаимодействия);
![]() и
и
![]() – скорости тех же тел после их
взаимодействия.
– скорости тех же тел после их
взаимодействия.
Кинетическая энергия тела, движущегося поступательно:
![]() ,
или
,
или
![]() .
.
Потенциальная энергия:
а) упруго деформированного тела:
![]() ,
,
где k – коэффициент упругости (жесткость) тела;
x– абсолютная деформация;
б) гравитационного взаимодействия тел:
![]() ;
;
в) тела, поднятого над поверхностью Земли:
![]() ,
,
где g– ускорение свободного падения;
h– высота тела над уровнем, принятым за нулевой (формула справедлива при условииh<<RЗ, гдеRЗ – радиус Земли).
Закон сохранения полной механической энергии (для замкнутой системы, где действуют консервативные силы):
W = Wк+WП= const.
Работа А, совершаемая внешними силами, определяется как мера изменения энергии системы (тела):A = W = W2 - W1
Работа:
а) постоянной силы F:
![]() ,
,
где - угол между направлениями силы![]() и перемещения
и перемещения![]() ;
;
б) переменной силы F:
![]()
в) упругой силы
![]() .
.
Мощность:
а) средняя за время t
![]() ;
;
б) мгновенная
![]() ,
или
,
или
![]() .
.
Момент инерции материальной точки
![]() ,
,
где r– расстояние от точки до оси вращения.
Момент инерции системы (тела):
![]() ,
или
,
или
![]() ,
,
где dm– элементарная масса тела;
dV– элементарный объем тела;
– плотность вещества тела.
Моменты инерции некоторых тел массой mотносительно оси, проходящей через центр масс (центр симметрии):
а) полого (тонкостенного) и сплошного цилиндров (или диска) радиуса R:
![]() ;
;
![]() ;
;
б) шара радиуса R:
![]() ;
;
в) тонкого стержня длиной l, если ось вращения перпендикулярна стержню:
![]() ;
;
то же, но ось вращения проходит через один из концов стержня:
![]() ;
;
г) тела относительно произвольной оси (теорема Штейнера):
![]() ,
,
где I0– момент инерции тела относительно оси, параллельной данной и проходящей через его центр инерции;
b– расстояние между параллельными осями.
Момент силы относительно неподвижной точки вращения:
![]() ,
или M = F d,
,
или M = F d,
где
![]() – радиус-вектор точки приложения силы;
– радиус-вектор точки приложения силы;
d– плечо силыF.
Момент импульса материальной точки относительно неподвижной точки:
![]() ,
или
,
или
![]() .
.
Основное уравнение динамики вращательного движения твердого тела:
![]() .
.
Проекция на ось Z момента импульса тела, вращающегося относительно неподвижной оси Z:
Lz
= Iz, или![]() ,
,
где - угловая скорость тела.
Закон сохранения момента импульса (количества движения) для изолированной системы:
![]() ,
,
где Ii– момент инерции тел относительно оси Zi;
i– угловая скорость вращения тел системы вокруг оси Z.
Кинетическая энергия вращающегося тела относительно неподвижной оси
![]() ,
или
,
или
![]() .
.
Работа силы при вращательном движении:
dA = Md,
где d– угол поворота тела.
Кинематическое уравнение гармонических колебаний материальной точки:
![]() ,
,
где х– смещение колеблющейся точки от положения равновесия;
А– амплитуда колебаний;
– круговая или циклическая частота;
0– начальная фаза колебаний;
t– время.
![]() ,
,
где Т– период колебаний точки;v– частота колебаний.
Скорость и ускорение
материальной точки, совершающей
гармонические колебания согласно
уравнения
![]() :
:
![]() –Asin(t+0);
–Asin(t+0);
![]() –A2cos(t+0)
= –2x.
–A2cos(t+0)
= –2x.
Сила, под действием которой точка массой mсовершает гармоническое колебание (возвращающая сила):
![]() ,
,
где
![]() (m– масса точки).
(m– масса точки).
Кинетическая и
потенциальная энергии колеблющейся
точки согласно уравнения
![]() :
:
![]() ;
; ![]() .
.
Полная энергия колеблющейся точки:
Е = Wк+WП=![]() .
.
Период собственных колебаний:
а) математического маятника
![]() ,
,
где l– длина маятника; g– ускорение свободного падения;
б) пружинного маятника
![]()
где m– масса колеблющегося тела;k– жесткость пружины;
в) физического маятника
![]() ,
,
где I– момент инерции колеблющегося тела относительно оси колебаний;
а– расстояние от центра тяжести маятника до оси колебаний;
![]() –приведенная
длина физического маятника.
–приведенная
длина физического маятника.
Уравнение затухающих
колебаний (в среде, где сила сопротивления
прямо пропорциональна
первой степени скорости,![]() )
)
x = Aoe-β tsin(t+1) илиx = Aoe-β tcos(t+2),
где А– амплитуда
в момент времениt = 0;е–
основание натурального логарифма;β=![]() –
коэффициент затухания.
–
коэффициент затухания.
Логарифмический декремент затухания
![]()
где Аt = Aoe-β t – амплитуда в момент времениt.
При сложении
гармонических колебаний одного
направления с одинаковой частотой
(периодом), но разными амплитудами и
начальными фазами
![]() ,
,![]() результирующее колебание описывается
уравнением:
результирующее колебание описывается
уравнением:
![]() ,
,
где
![]() – амплитуда результирующего
колебания;
– амплитуда результирующего
колебания;
![]() –его начальная
фаза.
–его начальная
фаза.
При сложении двух
взаимно перпендикулярных колебаний
одинакового периода, но разных амплитуд
и начальных фаз
![]() ,
,![]() ,
траектория результирующего колебания
задается уравнением:
,
траектория результирующего колебания
задается уравнением:
![]() .
.
В зависимости от разности фаз и амплитуд это будет либо прямая, либо эллипс, либо окружность.
Длина волны
![]() ,
,
где Т – период колебания;
![]() –скорость
распространения волны;
–скорость
распространения волны;
v– частота колебаний.
Уравнение плоской бегущей волны:
y =
Acos(t
– ![]() );
у= Acos(t
– kx),
);
у= Acos(t
– kx),
где y– смещение любой точки среды,x– расстояние точки от источника колебаний (рис. 1);
![]() –скорость
распространения колебаний в среде;
–скорость
распространения колебаний в среде;
![]() –волновое число;
–волновое число;
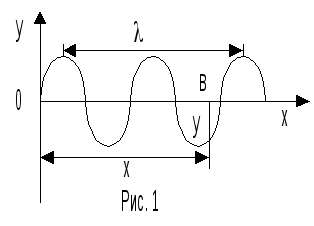
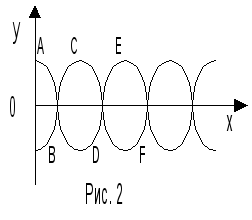 –длина волны.
–длина волны.
Р
Рис.
2 Рис.
1
![]() .
.
При падении плоской волны y1 = Asin(t –kx) на границу раздела двух сред возникает отраженная волна,y2 = Asin(t +kx) которая, складываясь с падающей волной, образует стоячую волну.
Уравнение стоячей волны у=у1+ у2:
y = 2Acoskxsint,
где A(x) = 2Acoskx– амплитуда стоячей волны.
