
- •Комплексні числа. Алгебраїчна, геометрична, тригонометрична і показникова форми запису комплексного числа. Дії над комплексними числами
- •Послідовності і ряди комплексних чисел. Степеневий ряд
- •Функції із с в с. Границя, неперервність
- •Похідна функції комплексної змінної. Умови диференційованості
- •Геометричний зміст модуля і аргументи похідної комплексної функції
- •Означення аналітичної функції. Поняття Конформного відображення
- •Лінійна функція
- •Дробово-лінійна функція
- •Степенева функція. Поверхня римана
- •Функція жуковського
- •Показникова функція комплексної змінної
- •Тригонометричні функції
- •Логарифмічна функція. Точка розгалудження
- •Радикал. Загальна степенева функція
- •Обернені тригонометричні функції
- •Інтеграл від функції комплексної змінної по кусочно-гладкому контуру
- •Теорема коші
- •Невизначений інтеграл. Формула ньютона-лейбніца
- •Формула коші. Принцип максимума модуля
- •Цілі функції. Теорема Ліувіля. Основна теорема алгебри
- •Розкладання функції в ряд Тейлора. Оцінка коефіцієнтів степеневого ряду
- •Нулі аналітичної функції. Ізольованість нулів. Теорема єдиності
- •Аналітичне продовження. Елементарні функції як аналітичні продовження
- •Розкладання аналітичної функції в ряд Лорана
- •Класифікація ізольованих особливих точок. Нескінченно віддалена особлива точка. Критерій особливої точки, яка усувається
- •Критерій полюса
- •Теорема Сохоцького-Вейєрштрасса
- •Раціональні і міроморфні функції
- •Означення ЛишкА. Обчислення лишків
- •Основна теорема теорії лишків
- •Застосування теореми лишків до обчислення визначених інтегралів
- •Зразки розв'язування задач з теорії функцій комплексної змінної
- •Контрольні роботи Денна форма навчання. 4 курс, 8 семестр Контрольна робота №1
- •Контрольна робота №2
- •Контрольна робота з теорії функції комплексної змінної для студентів 4 курсу (заочна форма навчання)
- •Література
Функції із с в с. Границя, неперервність
Комплексною функцією
комплексної змінної називається функція
![]() ,
у якої область визначення
,
у якої область визначення![]() та множина значень
та множина значень![]() належать множині комплексних чисел
належать множині комплексних чисел![]() .
Ці функції також можна вважати як
відображення із
.
Ці функції також можна вважати як
відображення із![]() в
в![]() .
.
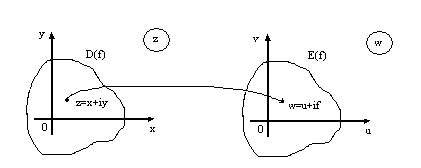
Частіше за все ми будемо
розглядати функції
![]() ,
у яких областю визначення є область.
,
у яких областю визначення є область.
![]() -окіл
-окіл
![]() –
–![]() – відкритий круг радіуса
– відкритий круг радіуса![]() з центром
з центром![]() .
.
О значення:
Множина
значення:
Множина
![]() називаєтьсяобластю,
якщо виконуються наступні умови:
називаєтьсяобластю,
якщо виконуються наступні умови:
кожна точка множини
 – внутрішня (існує
– внутрішня (існує -окіл
точки
-окіл
точки ,
всі точки якого належать
,
всі точки якого належать );
);будь-які дві точки множини
 можна з’єднати ламаною, всі точки якої
належать
можна з’єднати ламаною, всі точки якої
належать .
.
Приклад області:
![]()
Однозначна функція комплексної
змінної
![]() ,
яка задана в області
,
яка задана в області![]() ,
визначається законом, який ставить
кожному
,
визначається законом, який ставить
кожному![]() у відповідність одне визначене комплексне
число
у відповідність одне визначене комплексне
число![]() .
Символічно це записується
.
Символічно це записується![]() .
.
Оскільки кожне комплексне
число характеризується парою дійсних
чисел, то задання комплексної функції
![]() комплексної змінної
комплексної змінної![]() еквівалентне заданню двох дійсних,
тобто
еквівалентне заданню двох дійсних,
тобто![]() ,
,![]() ,
,
![]() визначені в області
визначені в області
![]() .
При цьому
.
При цьому![]() ,
а
,
а![]() .
.
Приклад:
![]() ,
,![]() ,
тобто
,
тобто![]() ,
,
![]() .
.
Означення:
Однозначна функція
![]() називаєтьсяоднолистковою
функцією в області
називаєтьсяоднолистковою
функцією в області
![]() ,
якщо в різних точках
,
якщо в різних точках![]() цієї області вона приймає різні значення.
цієї області вона приймає різні значення.
Далі ми будемо вважати, що
множина
![]() – значень функції
– значень функції![]() – область, тоді рівність
– область, тоді рівність![]() встановлює закон відповідності між
точками області
встановлює закон відповідності між
точками області![]() площини
площини![]() і точками області
і точками області![]() площини
площини![]() .
Тоді можливо встановити і обернену
відповідність – кожній
.
Тоді можливо встановити і обернену
відповідність – кожній![]() ставиться у відповідність одна або
декілька
ставиться у відповідність одна або
декілька![]() .
Це означає, що в
.
Це означає, що в![]() задана (однозначна або багатозначна)
функція
задана (однозначна або багатозначна)
функція![]() – обернена
– обернена![]() .
Відмітимо, що обернена функція до
однолисткової функції – однозначна.
.
Відмітимо, що обернена функція до
однолисткової функції – однозначна.
Приклад:
![]() ,
тоді обернена функція
,
тоді обернена функція![]() однозначна функція.
однозначна функція.
Нехай
![]() визначена на області
визначена на області![]() ,
а
,
а![]() – гранична точка
– гранична точка![]() .
.
Означення Коші:
![]() називаєтьсяграницею
називаєтьсяграницею
![]() при
при![]() ,
якщо
,
якщо![]()
![]() таке, що
таке, що![]() і такого, що
і такого, що![]() виконується нерівність
виконується нерівність
![]() .
.
Означення Гейне:
![]() називаєтьсяграницею
називаєтьсяграницею
![]() при
при![]() ,
якщо для будь-якої послідовності
,
якщо для будь-якої послідовності![]() ,
яка збігається до
,
яка збігається до![]() ,
послідовність
,
послідовність![]() збігається до
збігається до![]() .
Це записується
.
Це записується
![]() .
.
Теорема:
Нехай
![]() ,
,![]() гранична точка області визначення
гранична точка області визначення![]() .
Тоді для того, щоб
.
Тоді для того, щоб![]() необхідно і достатньо, щоб виконувались
співвідношення
необхідно і достатньо, щоб виконувались
співвідношення
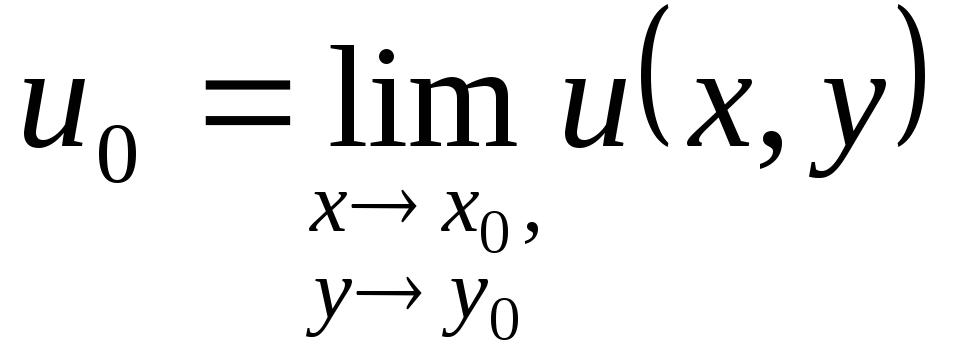 ,
,
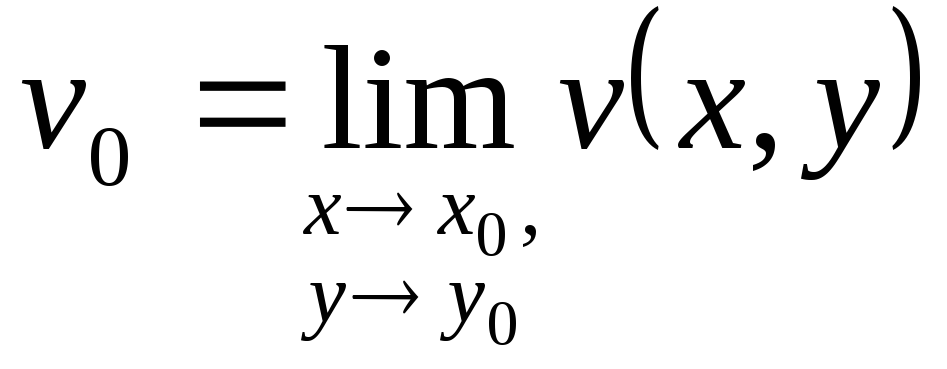 .
.
Доведеннядив. [2, с. 60].
З цієї теореми слідує виконання всіх властивостей границі функції аналогічні властивостям границі дійсних функцій.
Розглянемо функцію
![]() ,
тоді нескінченно віддалена точка
,
тоді нескінченно віддалена точка![]() визначається як точка, що відповідає
початку координат
визначається як точка, що відповідає
початку координат![]() при цьому
при цьому![]() .
.
Означення:
Функція
![]() називаєтьсянеперервною
в точці
називаєтьсянеперервною
в точці
![]() ,
якщо
,
якщо![]() .
.
Неперервність
![]() в
в![]() еквівалентна неперервності
еквівалентна неперервності![]() ,
,![]() в точці
в точці![]() .
.
Всі властивості неперервних
функцій аналогічні властивостям
неперервних функцій дійсної змінної
див. [2, 3]. Якщо функція
неперервна в кожній точці області
![]() ,
то кажуть, що вона неперервна на області
,
то кажуть, що вона неперервна на області![]() .
.
Приклад 1
![]() .
Знайти образ лінії
.
Знайти образ лінії
![]() .
.
Розв’язання
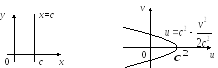
![]() ;
;
![]()
![]() при
при
![]() ,
,![]() ,
,![]() .
.
Тоді
![]() або
або![]() і підставляючи в
і підставляючи в![]() отримаємо
отримаємо![]() – парабола. Таким чином пряма
– парабола. Таким чином пряма![]() переходить при відображенні
переходить при відображенні![]() в параболу
в параболу![]() .
.
Приклад 2
![]() .
.
Розв’язання
![]() .
.
Вправи
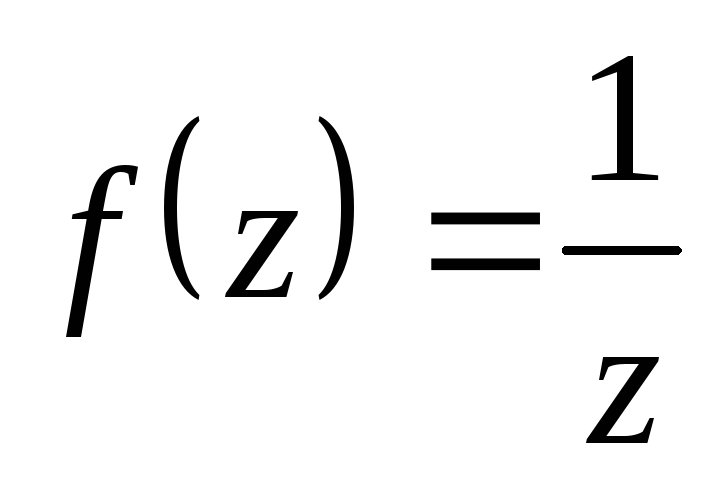 ,
,
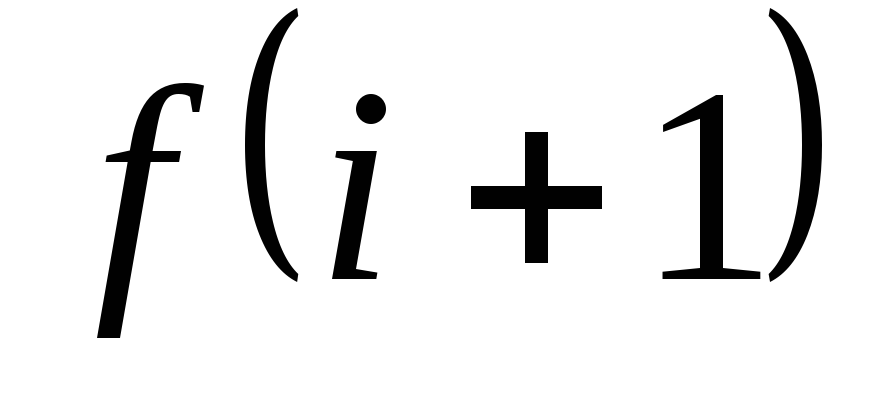 ,
,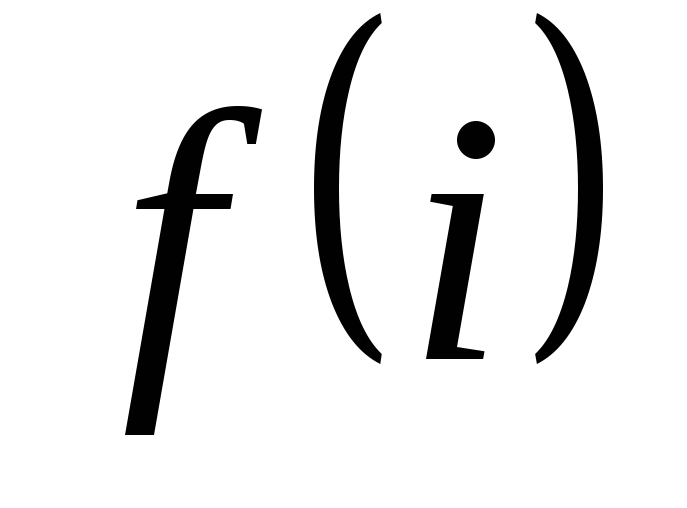 – ?
– ? .
Знайти образ
.
Знайти образ
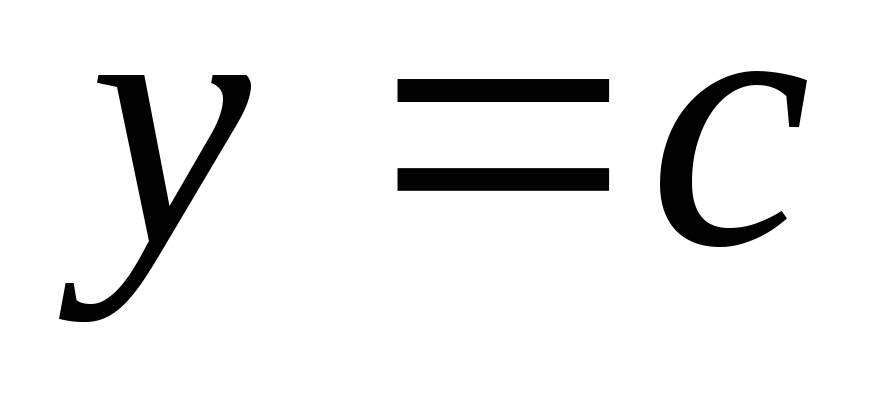 .
. .
Знайти образ
.
Знайти образ
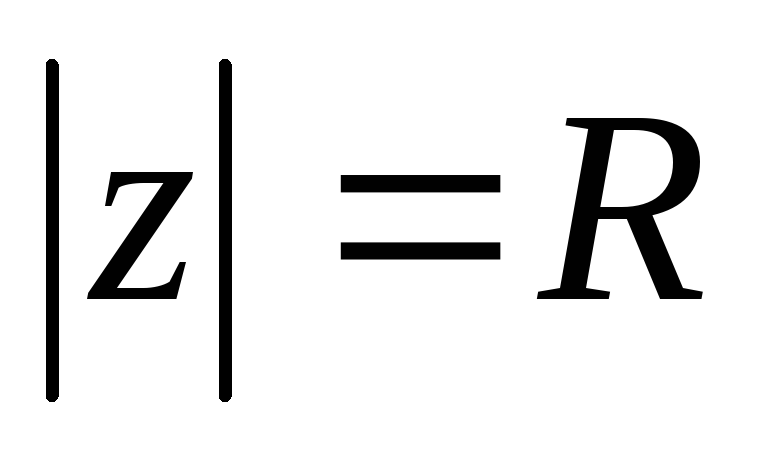 .
. .
Знайти образ
.
Знайти образ
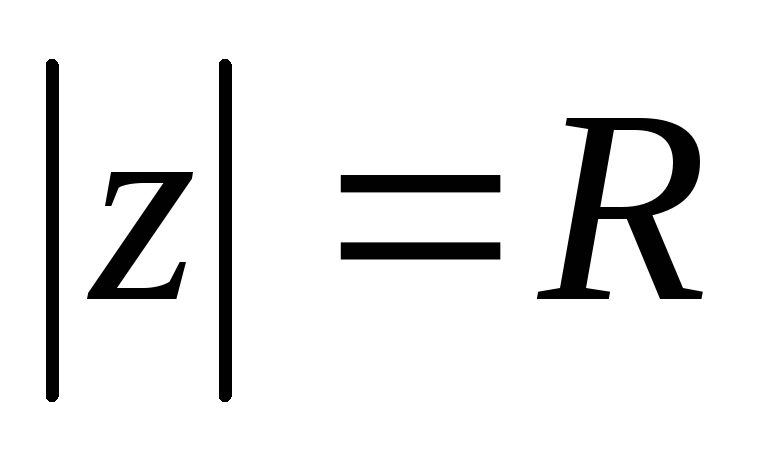 .
. .
Знайти образ
.
Знайти образ
 .
.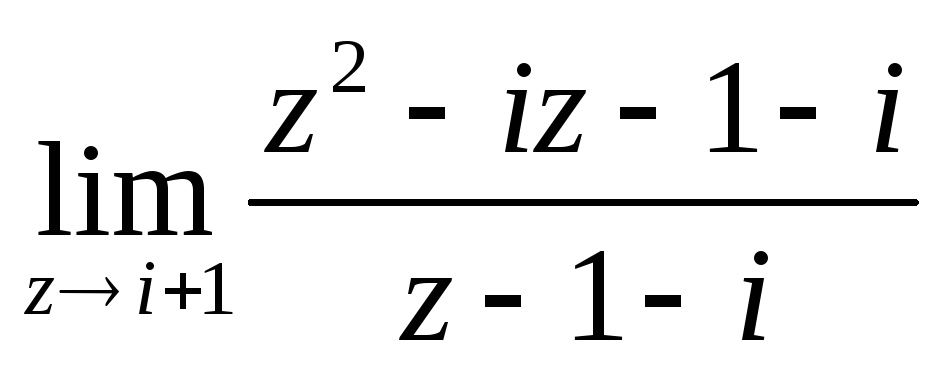 .
. .
.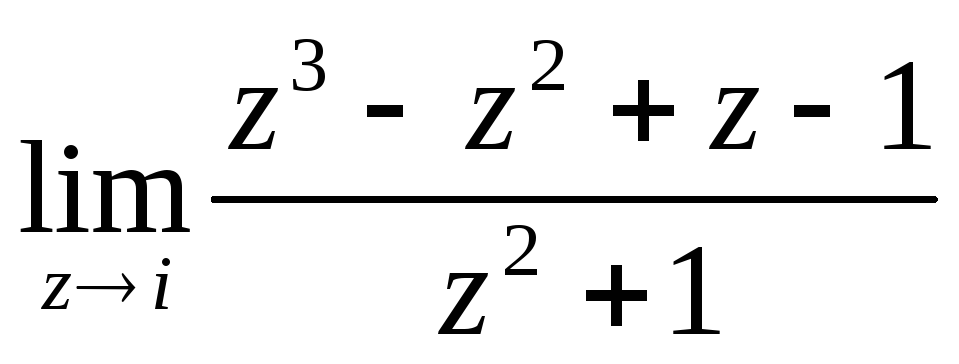 .
.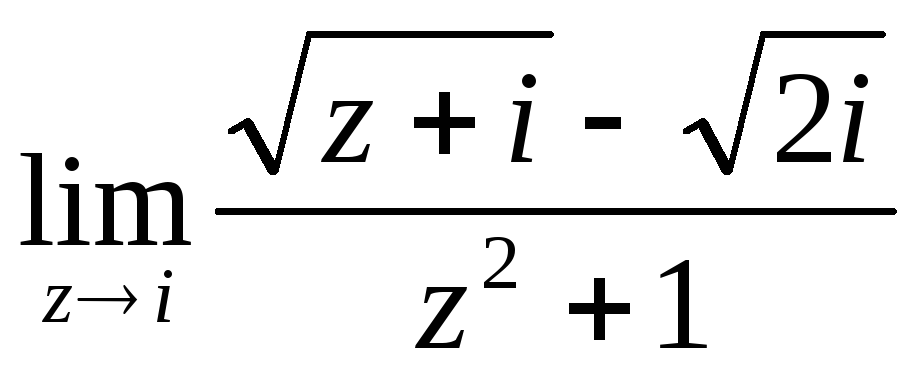 .
. .
.
Похідна функції комплексної змінної. Умови диференційованості
Нехай
![]() задана в області
задана в області![]() .
.
Означення:
Функція
![]() має в точці
має в точці![]() похідну,
якщо існує скінчена границя
похідну,
якщо існує скінчена границя
![]() .
.
Означення:
Функція
![]() називаєтьсядиференційованою
в точці
називаєтьсядиференційованою
в точці
![]() ,
якщо приріст функції
,
якщо приріст функції![]() в точці
в точці![]() має вигляд
має вигляд
![]() ,
,
де
![]() ,
,![]() нескінченно мала більш високого порядку
ніж
нескінченно мала більш високого порядку
ніж ![]() .
.
Як і у випадку дійсної функції
диференційованість в точці еквівалентна
існуванню скінченої похідної функції
в
![]() (див. [2]). Крім того, з диференційованості
функції в точці слідує її неперервність
в цій точці.
(див. [2]). Крім того, з диференційованості
функції в точці слідує її неперервність
в цій точці.
Безпосередньо із означення похідної слідує, що всі властивості похідної функції дійсної змінної виконуються і в нашому випадку.
Приклад 1
![]() ,
тоді
,
тоді
![]() .
.
Приклад 2
![]() .
Знайти
.
Знайти
![]() .
.
Похідну знайдемо за означенням
![]()
![]() ,
,
![]() ,
,![]() .
.
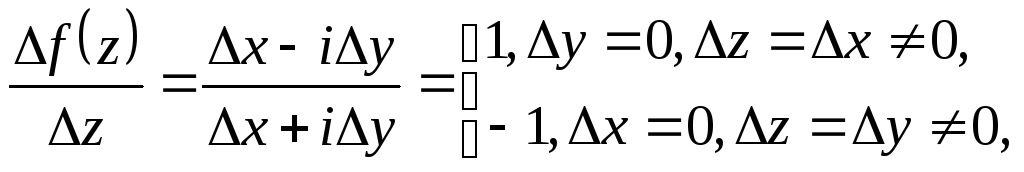 тобто границя
тобто границя
![]() не існує, а отже
не існує, а отже![]() не має похідної в точці
не має похідної в точці![]() .
.
У випадку, коли функція задана
в термінах
![]() ,
,![]() ,
тобто
,
тобто![]() ,
то диференційованість її, як умова
еквівалентна існуванню похідної по
,
то диференційованість її, як умова
еквівалентна існуванню похідної по![]() ,
перевірити важко. В цьому випадку корисна
наступна теорема.
,
перевірити важко. В цьому випадку корисна
наступна теорема.
Теорема.
Для того, щоб функція
![]() буда диференційованою в точці
буда диференційованою в точці![]() ,
необхідно і достатньо, щоб функції
,
необхідно і достатньо, щоб функції![]() ,
,![]() були диференційованими в точці
були диференційованими в точці
![]() як функції двох дійсних змінних
як функції двох дійсних змінних![]() і
і![]() та виконувалися умови Коші-Римана:
та виконувалися умови Коші-Римана:
![]() ,
,
![]() .
.
Доведення див. [1, с. 31] або [2, с. 85], [3, с. 33].
При цьому виконується рівність
![]() .
.
Означення:
Якщо функція
![]() диференційована у всіх точках області
диференційована у всіх точках області![]() ,
то
,
то![]() називаєтьсяаналітичною
в
називаєтьсяаналітичною
в
![]() .
.
Приклад 1
Дослідити на
диференційованість
![]() .
.
Розв’язання
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
тобто
,
тобто ![]() .
Отже,
.
Отже,
![]() не диференційована в
не диференційована в![]() .
.
Приклад 2
![]() .
Знайти
.
Знайти
![]() ,
якщо вона диференційована.
,
якщо вона диференційована.
Розв’язання
![]() ,
,
![]() ,
,
![]() .
Оскільки
.
Оскільки ![]() ,
,
![]() ,
то
,
то ![]() ,
,
![]() .
З останніх рівностей отримаємо, що
.
З останніх рівностей отримаємо, що
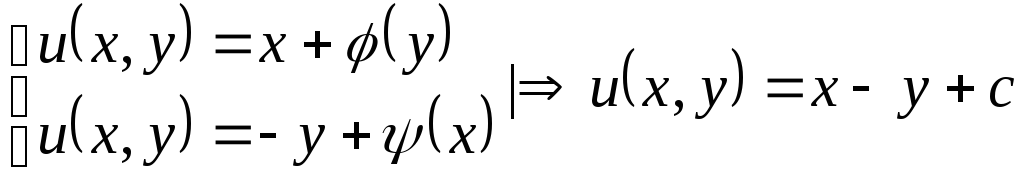 ,
,
![]() .
.
Вправи
Показати, що функції диференційовані
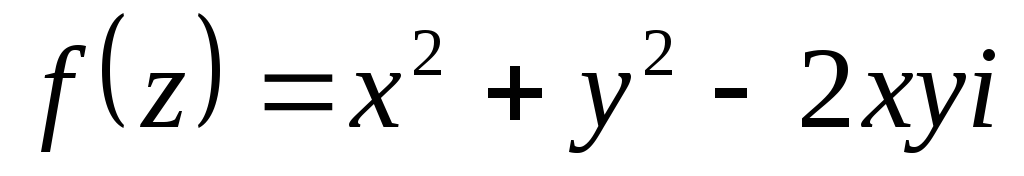 .
.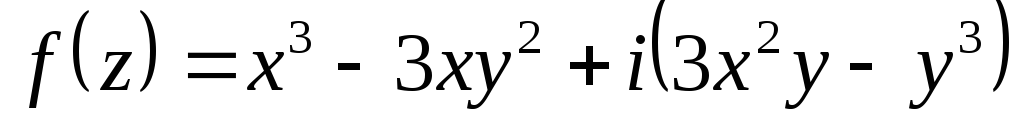 ,
,
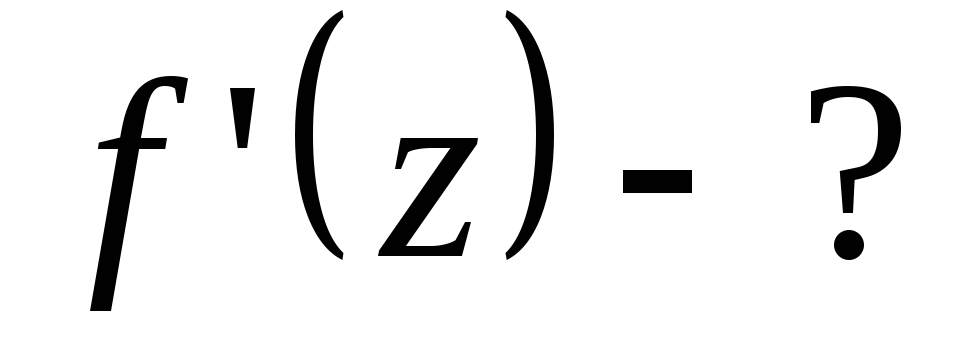
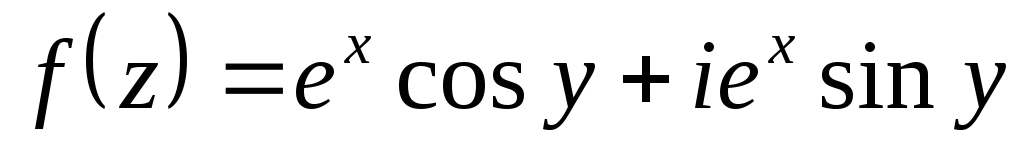 ,
,
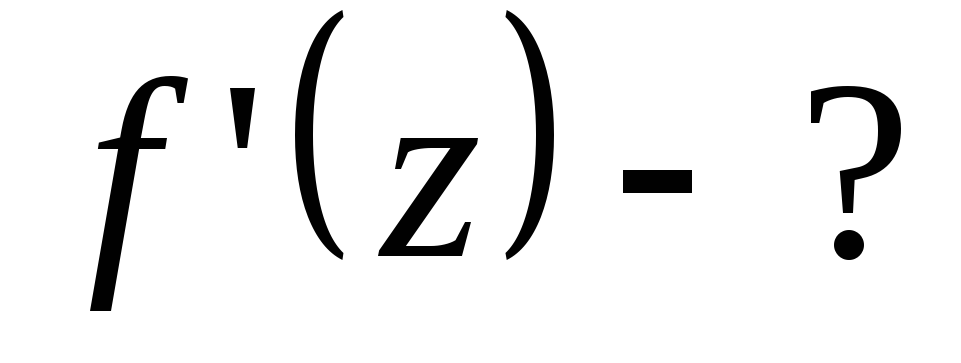
Довести, що функції не диференційовані.
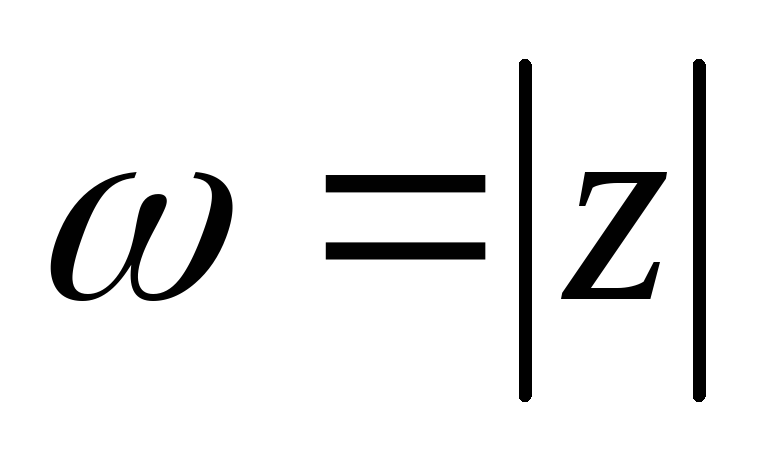 .
.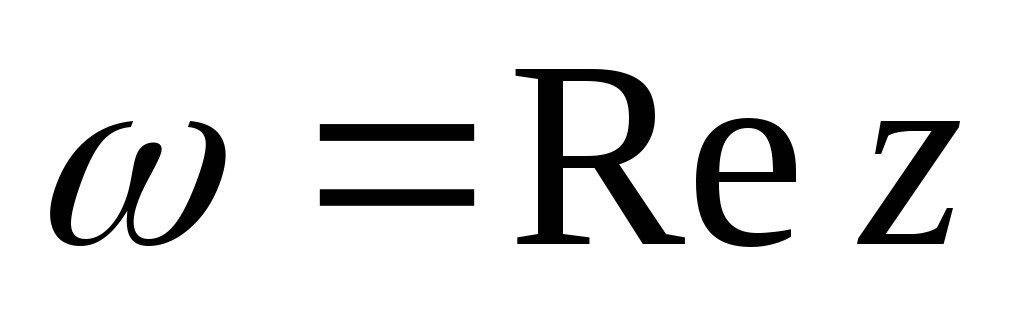 .
.Знайти
 ,
,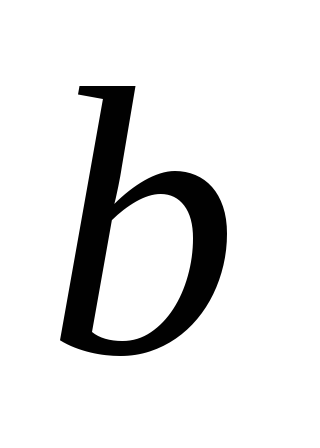 ,
, ,
при яких
,
при яких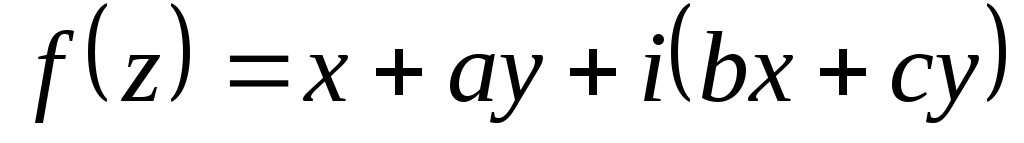 буде аналітичною.
буде аналітичною.
Знайти аналітичну функцію
![]() .
.
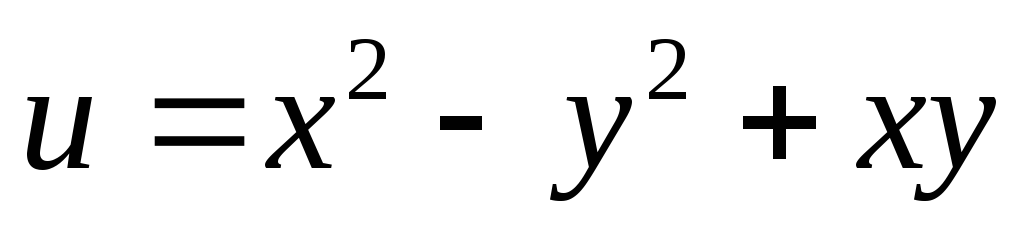 ,
,
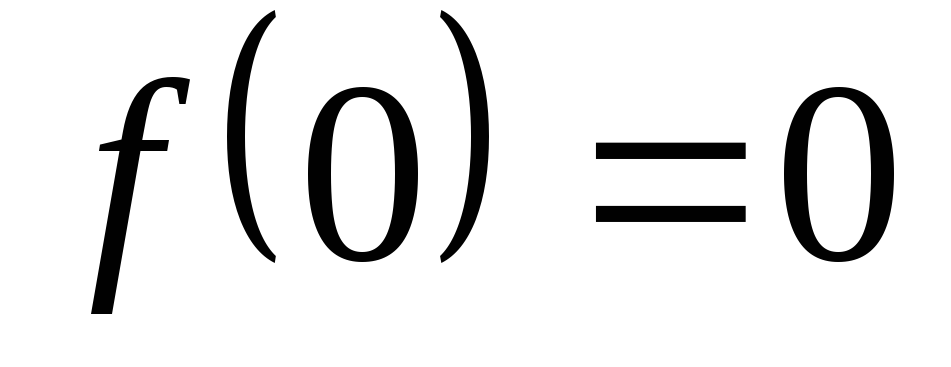 .
.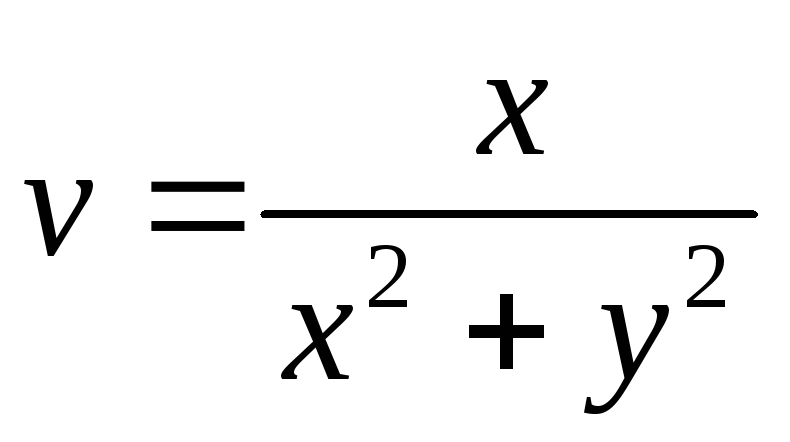 ,
,
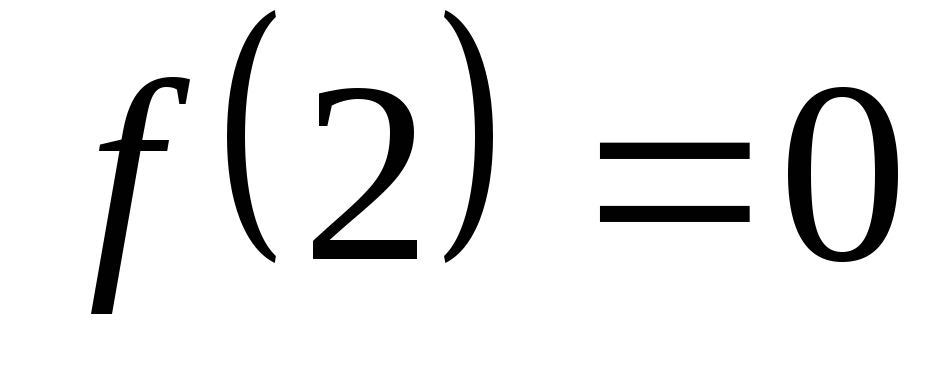 .
.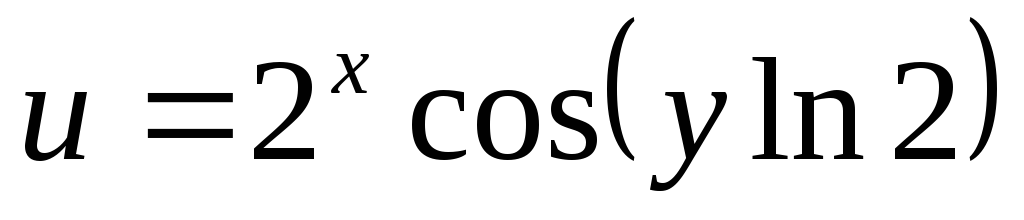 .
.При якому

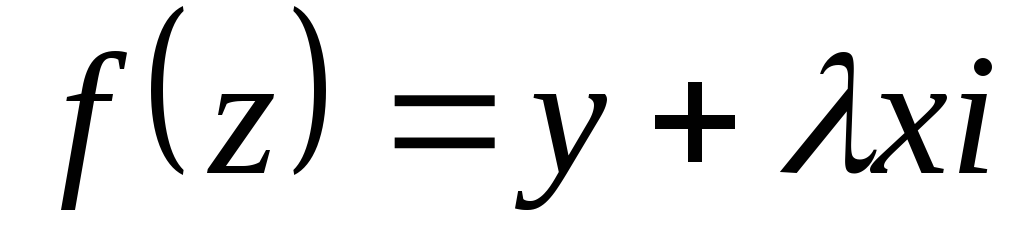 – аналітична?
– аналітична?
