Зразки розв’язання задач контрольної роботи № 3

І. Довести, що квадратні матриці порядку n з дійсними елементами утворюють векторний простір над полем дійсних чисел, якщо за операції взяти додавання матриць і множення матриці на число.

Розв’язання.Нехай м- множина всіх квадратних матриць порядку n з дійсними елементами. Покажемо, що м-абелева група відносно операції додавання.

1. Операція додавання матриць замкнена, тобто для .

Нехай ,, де

Тоді

Оскільки , то

2. Операція додавання матриць асоціативна, тобто

Дійсно, ,,

Оскільки – дійсні числа, то і тому .

3. У множині матриць M є матриця N, яка є нейтральним елементом відносно операції додавання матриць (нульовим елементом), тобто

.

Такою матрицею є нульова матриця, тобто

4. У множині матриць M існує для кожної матриці А протилежна матриця , тому.

Протилежною матрицею для даної матриці А є матриця

5. Операція додавання матриць комутативна.

Тоді для

Дійсно:

Оскільки для додавання дійсних чисел справедливий комутативний закон, то тобто

Покажемо тепер, що для множини М виконуються аксіоми векторного простору.

7. Для будь-якої матриціі чиселk,l,виконується рівність

[kl]

За означенням множення матриці на число

Оскільки дійсні числа, тотому

7.Для будь-якої матриці і дійсного числа 1.

Це випливає з означення множення матриці на число.

8. Операція множення матриці на число дистрибутивна відносно додавання матриць, тобто

Дійсно, ,

.

Оскільки – дійсні числа, то, тому.

9. Операція множення матриці на число дистрибутивна відносно додавання чисел, тобто

Справді, якщо ,, то за означенням множення матриці на число,

.

Оскільки – дійсні числа, то., тому.

Усі аксіоми векторного простору виконуються. Отже М – векторний простір над полем дійсних чисел .

II. Довести, що вектори ;;утворюють базис та знайти координати векторав цьому базисі.

Розв’язання. Оскільки розглядуваний простір має розмірність 3 (це ми визначили з кількості координат у заданих векторах), то досить довести, що система векторів лінійно незалежна. Обчислимо ранг матриці, складеної з координат цих векторів:

Легко бачити, що ранг цієї матриці дорівнює 3. Отже, система векторів лінійно незалежна і утворює базис.

Отже, кожний вектор можна розкласти за векторами цього базису, тобто, тоді числабудуть шуканими координатами векторав базисі.

Запишемо цю рівність в координатній формі: , тоді

. Звідси

отже, вектор в базисі е має координати (1, -3, 3), тобто.

III. Довести, що кожна з двох даних систем векторів є базисом і знайти зв’язок між координатами того самого вектора в цих двох базисах.

Розв’язання. Нехай В і В₁ – задані системи векторів. , де;;,, де;;.

Розглядуваний простір має розмірність 3.

Доведемо, що системи векторів В і В₁ лінійно незалежні. Обчислимо ранги матриць, складених відповідно з координат векторів

; ;

〜

〜

; .

Отже В і В₁ – базиси.

Знайдемо зв’язок між ними.

Кожний вектор простору однозначно лінійно виражається через вектори базису В.

Нехай (*)

Матриця , рядками якої є координатні рядки векторів базису В₁ в базисі В, і є матрицею переходу від базису В₁. знайдемо її. Запишемо рівності (*) в координатній формі:

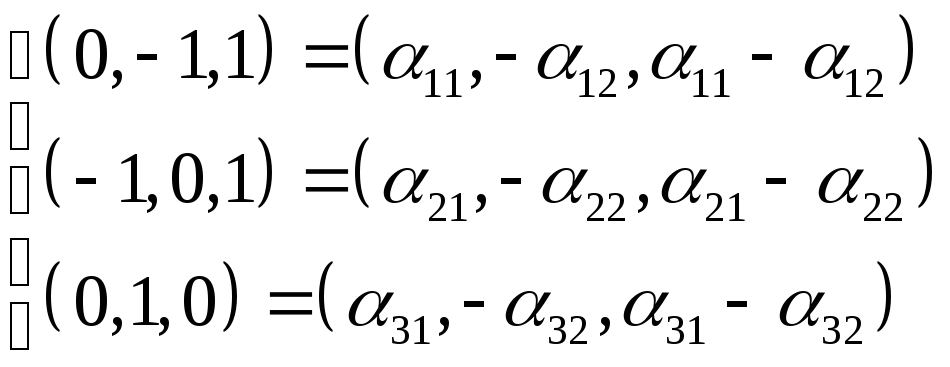
Звідси,

Розв’язуючи ці системи лінійних рівнянь, дістаємо:

отже матриця

для знаходження матриці Т^I переходу від базису В₁ до базису В можна було б скористатися тим же прийомом. Відомо проте, що . Знайдемо., отже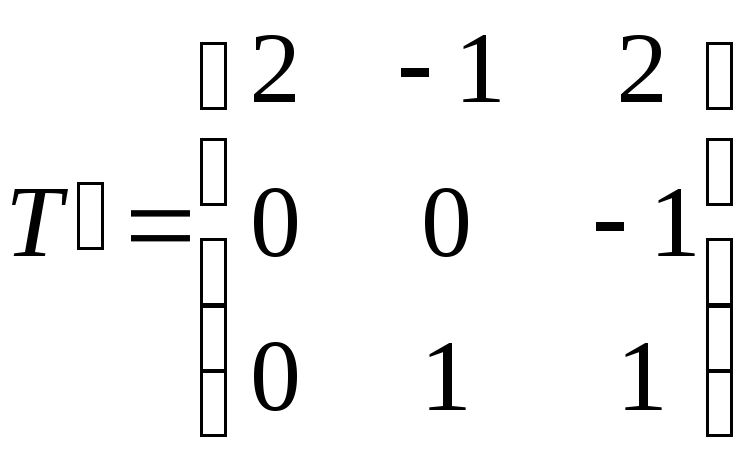

Звідси одержуємо:

IV. Знайти базиси суми і перетину векторних підпросторів V i U, заданих як лінійні оболонки векторів івідповідно.

Розв’язання. Нехай V=L;U=L’. Базисом В сумиS=V+U є кожна максимальна лінійно незалежна підсистема системи векторів .

Знайдемо спочатку базиси підпросторів V і U.

Нехай за умовою ,,,,,.

Складаємо матриці А і С з координат заданих векторів та обчислюємо їх ранги.

,

,

Отже, базисом простору V є система векторів , а базисом просторуU є система векторів . Знайдемо базис В просторуV+U.

Складаємо матрицю В з координат векторів і знаходимо її ранг:

за базис простору S можна взяти такі вектори: .

Знайдемо тепер базис перетину .

Оскільки ;;, то очевидно.

Отже базис простору Р складається з двох векторів. Знайдемо їх. Оскільки простір Р складається з тих і тільки тих векторів , які належать як до просторуV так і до простору U, то (1)

Ця рівність еквівалентна системі чотирьох лінійних однорідних рівнянь з невідомими рангу 4.

+

Знаходимо фундаментальну систему розв’язків цієї системи.

Оскільки перші чотири стовпчики матриці цієї системи лінійно незалежні (вони є координатами векторів , то за вільні невідомі можна взяти останніі. Тоді

звідси дістаємо загальний розв’язок системи:

, ,,.

Узявши послідовно, ;і;, дістаємо фундаментальну систему розв’язків

;

базис простору Р дістанемо, якщо в рівності (1) замість (або замість) підставимо їх значення зі. Одержуємо:

і остаточно:

V. На вектори натягнута лінійна оболонкаL.

а) побудувати ортонормований базис підпростору L;

б) знайти ортогональне доповнення ;

в) знайти відповідно проекції y i z вектора х на підпростори і;

г) знайти кут між вектором х і підпростором ;

д) знайти відстань між вектором і підпростором.

Розв’язання.

а) знаходимо розмірність і базис підпростору . Складаємо матрицю із координат векторіві обчислюємо її ранг.

〜

〜

;

отже, , і векториутворюють лінійно незалежну систему, тобто є базисом підпростору.

Застосуємо до векторів процес ортогоналізації. За перший векторвізьмемо вектор:

.

Вектор шукаємо у формі лінійної комбінації векторіві:

=+.

Оскільки повинен бути ортогональним до,

;

звідки ;

отже, .

Вектор шукаємо у формі лінійної комбінації векторіві.

;

оскільки ортогональний доі до, то

звідки

.

Отже, =(9, -3, -5, 3).

Побудували нову систему попарно ортогональних ненульових векторів:

=(1, 2, 3, 4)

=(-1, 3, -3, 1)

=(9, -3, -5, 3), яка є лінійно незалежною, отже, ортогональним базисом підпростору .

Побудуємо ортогоналізований базис підпростору . Знаходимо норми векторів.

;

отже, ортонормованим базисом є система векторів:

=

=.

б) Щоб знайти ортогональне доповнення підпростору, що є лінійною оболонкою векторівдостатньо знайти базис.

Відомо, що вектор ортогональний до будь-якого вектора з підпросторутоді і тільки тоді, коли він ортогональний до кожного вектора деякого базису цього простору.

Вектори лінійно незалежні (доведено вище), тому утворюють базис.

Нехай вектор – довільний вектор з ортогонального доповненняпідпростору.

і .

Тоді мають місце співвідношення:

; ;.

Запишемо ці рівності у вигляді системи однорідних рівнянь:

всі розв’язки цієї системи утворюють підпростір. Знайдемо його базис, тобто фундаментальну систему розв’язків. Ранг матриці цієї системи дорівнює 3, отже фундаментальна система розв’язків складається з 4-1=3 вектора.

Нехай . Тоді маємо:

〜

〜

отже, вектор є базис ортогонального доповненняпідпростору.

Оскільки кожен вектор із є лінійною комбінацією базису, то.

в) знайдемо відповідно проекції івекторана підпросториі.

Оскільки , то вектормає єдине зображення=+, де,.

Враховуючи, що L – лінійна оболонка, натягнута на вектори , маємо

, тоді

(*).

Обидві частини рівності (*) скалярно помножуємо на вектори , і враховуючи, що (,) = (,) = (,) = 0, маємо:

Одержуємо систему рівнянь:

або

розв’язуючи систему рівнянь, знаходимо:

; ;.

Отже,

Отже, проекція наL:, проекціяна:.

г) Оскільки - проекція векторана підпростірL, обчислюємо за формулою:

д) Відстань

VI. Довести, що множення кожної квадратичної матриці другого порядку з дійсними коефіцієнтами зліва на матрицю є лінійним оператором векторного простору всіх квадратичних матриць другого порядку над полем дійсних чисел R.

Знайти матрицю цього лінійного оператора у базисі із матриць

Розв’язання. Нехай A-оператор множення кожної квадратичної матриці другого порядку зліва на матрицю . Перевіряємо, чи буде він лінійним. Розглянемо образ суми двох матриць Х і У, де. Маємо

A (X+Y) 

A X 

A Y 

A X+A Y 

Отже, A (X+Y)= A X+A Y.

Нехай тепер -довільне ціле число. Тоді A (X)(A X)

Звідси випливає: оператор A – лінійний.

Знайдемо його матрицю в заданому базисі.

Для цього знаходимо образи базисних векторів під дією оператора A.

A 

A 

A 

A 

Матрицею А лінійного оператора A буде матриця

VII. Нехай лінійний оператор A в базисі має матрицю, а лінійний операторB в базисі має матрицю. Знайти матрицю Х лінійного оператораA B в базисі, в якому задано координати всіх векторів.

Розв’язання. Позначимо матрицю лінійного оператора A в базисі e, в якому задані координати всіх векторів, через , а оператораB – через . Тоді, деT₁ і T₂ – матриці переходів від базисів a i b до базису e відповідно. Оскільки матриці і, рядками яких є координати векторів базисівa i b відповідно, є матрицями переходу від базису е до базисів a i b, то ,

Виконаємо обчислення:

Відповідь:.

VIII. Побудувати ядро KerA, область значень ImA та знайти ранг , дефект лінійного оператораA -векторного простору L₃, який у деякому базисі цього простору задано матрицею.

Розв’язання. Оскільки ранг лінійного оператора A дорівнює рангу матриці А, знайдемо r(A): . Звідси r(A)=2, і тому dim(ImA )=2, тобто ранг лінійного оператора A дорівнює 22. Виходячи з рівності dim(ImA )+dim(KerA )=n, одержуємо dim(KerA )=3–2=1, тобто дефект лінійного оператора А дорівнює 1. Для побудови KerA і ImA достатньо знайти їх базиси.

Оскільки ImA = < xAR³ >, , , , то підпростір породжується системою векторівe₁A, e₂A, e₃A.

Знаходимо ці вектори:

e₁A =(1,2,3); e₂A =(2,–1,1); e₃A =(1,0,1).

Ранг цієї системи векторів дорівнює r(A)=2, отже, максимальна лінійно незалежна підсистема цієї системи векторів складається з двох векторів. За цю систему можна взяти вектори e₁A  і e₂A ; отже, ImA  складається з векторів e₁A =(1,2,3); e₂A =(2,–1,1).Тоді ImA .

Побудуємо KerA. Оскільки KerA , тоKerA є множина тих векторів простору R³, координатні рядки яких у базисі утворюють простір розв’язків системи лінійних однорідних рівнянь [x]A=[], або

Оскільки матриця цієї системи є матрицею, транспонованою до матриці А, то ранг цієї системи дорівнює 2. За вільне невідоме обираємо х₁. Тоді , і фундаментальною системою розв’язків підпростору розв’язків цієї системи є вектор

Тоді Ker A.

Відповідь: ImA .KerA .dim(ImA )=2; dim(KerA )=1.

IX. Знайти власні значення і власні вектори лінійного оператора A, заданого в деякому базисі B=<b₁,b₂,b₃> цього простору матрицею

Розв’язання.

Характеристичне рівняння оператора, заданого матрицею А має вигляд

Розв’язавши його, одержуємо

Усі корені – дійсні числа, отже лінійний оператор має три власних значення:

Знайдемо власні векторі, що відповідають цим значенням.

Нехай Маємо наступну систему лінійних однорідних рівнянь:

або r=2;

Фундаментальна система розв’язків складається із одного вектора

Отже, всі власні вектори, що належать власному значенню мають вигляд

тобто всі ненульові вектори, що належать підпростору L₁, що натягнутий на вектор (1,0,1).

Для маємо наступну систему лінійних однорідних рівнянь.

або

r=2

Фундаментальна система розв’язків складається з одного вектора x”=(0,1,0), тоді всі власні вектори, що належать власному значенню мають вигляд

тобто, всі ненульові вектори, які належать підпростору, натягнутому на вектор (0,1,0).

Для маємо систему рівнянь:

або

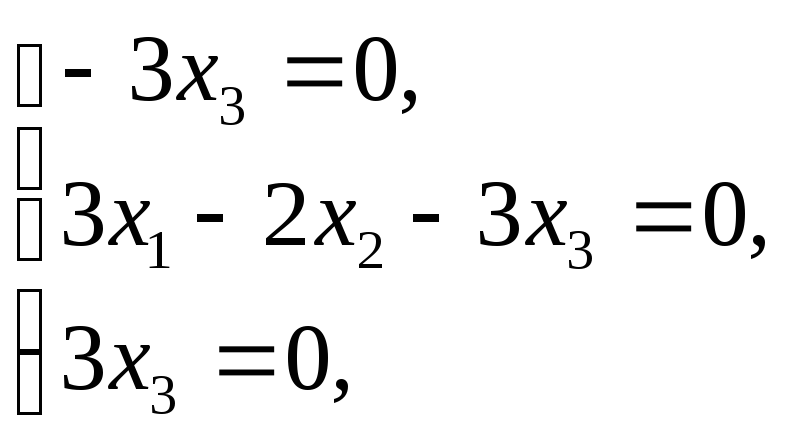r=2.

Фундаментальна система розв’язків є вектор

.

Тоді власні вектори, що належать власному значенню , мають вигляд:

Тобто всі ненульові вектори, що належать підпростору L₂, натягнутому на вектор (-2,3,0).

Отже, лінійний оператор, заданий матрицею А, має три різних власних значення і відповідні ним власні вектори, ненульові вектори з лінійних оболонок L₁,L₂,L₃, натягнутих на вектора (1,0,1), (0,1,0), (-2,3,0).

Х. Чи зводиться матриця лінійного оператораA векторного простору V₃ до діагонального вигляду за допомогою переходу до іншого базису? Знайти цей базис і відповідну йому матрицю.

Розв’язання. Достатньою умовою для зведення матриці лінійного оператора векторного простору розмірності n є наявність у даного оператора n різних власних значень (оператор повинен мати простий спектр), причому діагональними елементами будуть саме ці власні значення.

У матриці А всі власні значення різні і їх три:

Отже, матриця А зводиться до діагональної матриці

.

Визначимо базис, в якому матриця А має діагональний вид А₁.

Оскільки цей процес зводиться до знаходження власних векторів оператора, то маємо такий базис для матриці А₁:

Відповідь: