Зразки розв’язання задач контрольної роботи №1

1.

1) Довести, що з половини діагоналей будь-якого чотирикутника і будь-якої із його середніх ліній можна скласти трикутник.

Розв’язання.

Нехай АВСD – деякий чотирикутник

М-середина відрізка АВ, N- середина СD.

Тому

Отже, відповідно до умови замкненості, відрізки з довжинами ;іутворюють трикутник.

2) Довести, що три висоти трикутника перетинаются в одній точці.

Розв’язання.

Нехай АН₁ і ВН₂ – висоти трикутника АВС ; Н – точка перетину цих висот. Через точку Н проведемо пряму СН до перетину з АВ в точці К. Позначимо

, ;. Тоді;;.

Мають місце рівності: ;.

Звідси .Отже, відрізок СК перпендикулярний відрізку АВ і

2.

Знайти точку, симетричну з точкою Q(3,7) відносно прямої 3x-4y+10=0

Розв’язання

Точка, симетрична точцілежить на перпендикулярідо прямої, причому QO=QO’. Тому:

1)Знаходимо рівняння прямої :

2)Знаходимо координати точки О:

Отже О.

3)Знаходимо коордитнати точки :

Отже.

3.

Знайти відстань між прямими 3x-4y+5=0 і 6x-8y-13=0

Розв’язання

Прямі іпаралельні, так як. На прямійдовільно обираємо точку М(1,2); знаходимо її відстань від прямої. Зводимо рівняння прямоїдо нормального виду ; нормуючий множник

Отже, нормальне рівняння прямої :

Знаходимо відстань т. М від прямої ;;

Відповідь: .

4.

З усіх прямих, що перетинають дві прямі ;,

знайти ту, що паралельна прямій

Розв’язання

1.Запишемо рівняняя шуканої прямої у вигляді

2.Умова перетину цієї прямої з даними прямими:

;

Обчислюємо визначники:

; або

; або

Одержуємо систему рівнянь: Нехай Z₀=2;

Тоді

Отже рівняння шуканої прямої:

Відповідь: .

5.

Знайти відстань між прямими:

; ;

Розв’язання

Точка ;

Точка

Направляючі вектори прямих івідповідно.

Тоді d-відстань між прямими і.

6.

Через пряму провести площину, перпендикулярну до площини 2x-3y+5z-1=0.

Розв’язання

Так як площина проходить через задану пряму, то будь-яка точка цієї прямої належить цій площині. Отже, рівняння площини записуємо у вигляді:

A(x-3)+B(y+1)+C(z-1)=0

Нормальний вектор

Направляючий вектор прямої

Так як шукана плошина перпендикулярна до даної площини, то маємо

2А-3В+5С=0

Вектори іперпендикулярні, тому

3А+2В+5С=0

Розв’язуємо систему рівнянь:

Підставляємо знайдені значення у рівняння шуканої площини:

Скорочуємо на –В:

Отже, 25x-5y-13z-67=0 – рівняння шуканої площини.

Відповідь: 25x-5y-13z-67=0.

7.

До гіперболи провести таку дотичну, яка знаходилась би на однаковій відстані від центра і від правого фокуса.

Розв’язання

1. Нехай М(x₀,y₀) – точка дотику, тоді рівняння дотичної має виглядабо.

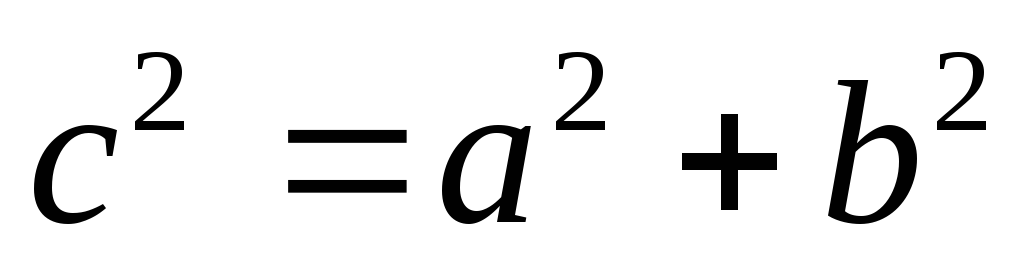
2. Знайдемо координати правого фокуса отже

3. Знайдемо відстань d₁ від центра до дотичної:

4. Знайдемо відстань d₂ від до дотичної

5. За умовою, d₁=d₂ тому звідси

6. Знаходимо y₀ ; так як М належить гіперболі, то маємо ;

Отже одержуємо дві точки дотику:

7. Запишемо рівняння дотичної

а)

б)

Відповідь:

8.

Скласти рівняння еліпса, якщо відстань між директрисами дорівнює 16; і ексцентриситет

Розв’язання.

Рівняння еліпса -

Необхідно знайти а і b.

- рівняння директрис.

За умовою маємо:

Для еліпса

Отже, рівняння еліпса:

Відповідь:

9.

Визначити вид поверхні та знайти її найпростіше рівняння:

2x²+3y²+5z²-4z-6y+10z-1=0