
- •С. Колеснік
- •Збірник контрольних робіт. Аналітична геометрія та лінійна
- •Контрольна робота № 1
- •Зразки розв’язання задач контрольної роботи №1
- •Розв’язання
- •Контрольна робота № 2
- •Зразки розв’язання задач контрольної роботи №2
- •Контрольна робота № 3
- •1. Перевірити чи утворюють наступні множини векторні простори над полем дійсних чисел r
- •Зразки розв’язання задач контрольної роботи № 3
- •Розв’язання.Нехай м- множина всіх квадратних матриць порядку n з дійсними елементами. Покажемо, що м-абелева група відносно операції додавання.
- •Контрольна робота № 4
- •Зразки розв’язання задач контрольної роботи № 4 і. Для квадратичної форми fзнайти:
- •Контрольна робота №5.
- •Зразки розв’язання задач контрольної роботи №5
- •Контрольна робота № 6
- •Зразки розв’язання задач контрольної роботи № 6
- •Контрольна робота №7
- •Зразки розв’язання задач контрольної роботи № 7
- •Контрольна робота № 8.
- •Зразки роз`язання задач контрольної роботи № 8
- •Для простого модуля старший коефіцієнт взаємнопростий з ним. Визначимо множник k так, щоб . Матимемо . Домножаючи обидві частини заданої конгруенції на 10 за модулем 13, дістаємо
- •Контрольна робота № 9
- •Зразки розв‘язання задач контрольної роботи № 9
- •Тоді з рівності
- •Додаток: таблиці первісних коренів та індексів
- •Література
- •Методичне видання
Контрольна робота № 8.
Р
озв`язати конгруенції:
 ,
, (mod
5),
(mod
5), (mod
7),
(mod
7), (mod
11),
(mod
11), (mod
11),
(mod
11), (mod
3),
(mod
3), (mod
5),
(mod
5), (mod
5),
(mod
5), (mod
5),
(mod
5), (mod
5).
(mod
5).
Розв`язати конгруенції, звівши їх до двочленних:
 (mod
5),
(mod
5), (mod
17),
(mod
17), (mod
31),
(mod
31), (mod
41),
(mod
41),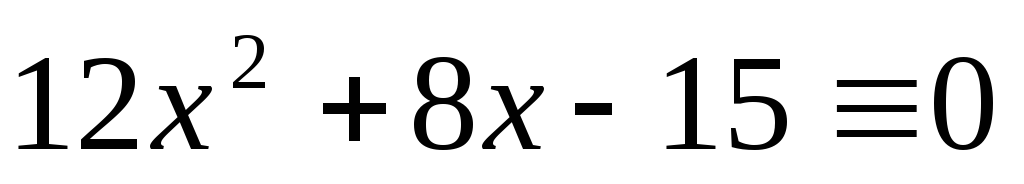 (mod
47),
(mod
47), (mod
13),
(mod
13), (mod
23),
(mod
23), (mod
5),
(mod
5), (mod
7),
(mod
7), (mod
7).
(mod
7).
Користуючись критерієм Ейлера знайти всі квадратні лишки за модулем:
5;
7;
11;
13:
17;
23;
37;
53;
19;
43.
Знайти порядок числа a за модулем m, якщо:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
a |
5 |
2 |
4 |
10 |
2 |
7 |
3 |
4 |
5 |
5 |
|
m |
13 |
5 |
5 |
13 |
17 |
43 |
7 |
7 |
7 |
11 |
Знайти всі первісні корені за модулем m:
|
варіант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
m |
7 |
11 |
13 |
17 |
19 |
23 |
29 |
31 |
37 |
41 |
Розв`язати конгруенції:
 (mod
7),
(mod
7), (mod
13),
(mod
13), (mod
23),
(mod
23), (mod
31),
(mod
31), (mod
37),
(mod
37), (mod
61),
(mod
61), (mod
73),
(mod
73), (mod
73),
(mod
73), (mod
73),
(mod
73), (mod
79).
(mod
79).
Знайти найменше натуральне число x, яке задовольняє наступній конгруенції:
 (mod
13),
(mod
13), (mod
17),
(mod
17), (mod
31),
(mod
31), (mod
31),
(mod
31), (mod
31),
(mod
31), (mod
37),
(mod
37), (mod
41),
(mod
41), (mod
43),
(mod
43), (mod
53),]
(mod
53),] (mod
67).
(mod
67).
Знайти остачу від ділення;
 на
35;
на
35; на
29;
на
29; на
37;
на
37; на
29;
на
29; на
67;
на
67; на
73;
на
73; на
79;
на
79;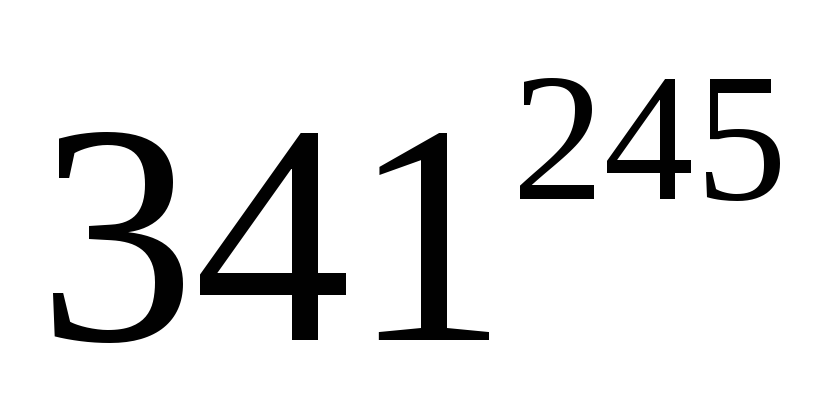 на
89;
на
89; на
629;
на
629; на
135.
на
135.
Зразки роз`язання задач контрольної роботи № 8
Розв`язати конгруенцію:
![]() (mod
5).
(mod
5).
Розв`язання.
Конгруенцію замінимо еквівалентною їй конгруенцією степеня не вище 4 за тим же самим модулем 5.
Поділимо
![]() на
на![]() .
Дістанемо
.
Дістанемо![]()
Замінивши
всі коефіцієнти остачі найменшими
лишками за модулем 5, дістанемо, що дана
конгруенція еквівалентна конгруенції
![]() (mod
5). (1)
(mod
5). (1)
Замінимо цю конгруенцію еквівалентною їй конгруенцією із старшим коефіцієнтом, що дорівнює 1. Розв`яжемо конгруенцію:
![]() (mod
5).
(mod
5).
Додамо до правої частини модуль:
![]() (mod
5).
(mod
5).
Обидві частини ділимо на 3:
![]() (mod
5).
(mod
5).
Домножимо конгруенцію (1) на 2:
![]() (mod
5).
(mod
5).
Останню конгруенцію замінимо еквівалентною їй:
![]() (mod
5).
(2)
(mod
5).
(2)
О скільки
скільки![]() (mod
5),
то (x,
5)=1,
а тому
(mod
5),
то (x,
5)=1,
а тому
![]() (mod
5).
Тоді конгруенція (2) матиме вигляд
(mod
5).
Тоді конгруенція (2) матиме вигляд
![]() (mod
5).
(3)
(mod
5).
(3)
Оскільки (x, 5)=1, то обидві частини конгруенції (3) можна скоротити на x:
![]() (mod
5)
(4)
(mod
5)
(4)
Конгруенція (4) має такі розв`язки:
![]() (mod
5)
і
(mod
5)
і
![]() (mod 5).
(mod 5).
Отже, конгруенція (1) має розв`язки:
![]() 2;
3 (mod
5).
2;
3 (mod
5).
Зауваження:
Замість того, щоб ділити
![]() на
на![]() ,
можна було б замінити
,
можна було б замінити![]() на
на![]() ,
деr
– остача від ділення s
на 5-1= 4, причому якщо s
ділиться на 4, то покладаємо r=4.
Тоді
,
деr
– остача від ділення s
на 5-1= 4, причому якщо s
ділиться на 4, то покладаємо r=4.
Тоді
![]() (mod
5);
(mod
5);
![]() ;
;
![]() ;
;
![]() .
.
Отже,
![]() .
.
Розв`язати конгруенцію, звівши її до двочленної:
 .
.
Розв`язання.
Для простого модуля старший коефіцієнт взаємнопростий з ним. Визначимо множник k так, щоб . Матимемо . Домножаючи обидві частини заданої конгруенції на 10 за модулем 13, дістаємо
![]() ,
,
або
![]() .
.
Виділимо в лівій частині цієї конгруенції повний квадрат
![]() ,
,
або
![]() .
.
Остаточно
![]() .
.
Отже,
![]() або
або![]() .
.
За критерієм Ейлера знайти всі квадратні лишки за модулем 11.
Розв`язання.
За
критерієм Ейлера при простому непарному
p
число a
є квадратичним лишком за модулем p
тоді і тільки тоді, коли
![]() ,
і квадратичним нелишком тоді і тільки
тоді, коли
,
і квадратичним нелишком тоді і тільки
тоді, коли![]() .
.
Отже, для розв`язання задачі випробуємо числа 1, 2, 3, .., 10 за допомогою критерія Ейлера. Маємо
![]() ,
тоді
,
тоді
 (mod
11).
(mod
11).
Тому числа 1, 3, 4, 5, 9 – квадратичні лишки за модулем 11.
Знайти порядок числа a = 2 за модулем m = 15.
Розв`язання.
Щоб
знайти порядок
![]() числа
a
за
модулем m,
необхідне виконання таких вимог:
числа
a
за
модулем m,
необхідне виконання таких вимог:
(a, m)=1;
 -
дільник
числа
-
дільник
числа
 ;
; -
найменше з тих натуральних чисел k,
для яких виконується конгруенція
-
найменше з тих натуральних чисел k,
для яких виконується конгруенція
 .
.
Маємо
(2, 15)=1; знаходимо
![]() :
:
![]() =
=![]() .
.
Отже,
![]() міститься серед чисел 1, 2, 4, 8. Записуємо
послідовно:
міститься серед чисел 1, 2, 4, 8. Записуємо
послідовно:
![]()
,
![]() ,
,
![]() .
.
Отже,
![]() =4.
=4.
Знайти всі первісні корені за модулем m=7.
Розв`язання.
Первісних
коренів за простим модулем m=7
є
![]() .
Вони містяться серед чисел
.
Вони містяться серед чисел![]() :
:
![]() .
.
Оскільки
m-1=6
у канонічному розкладі має вигляд
![]() ,
то досліджувати слід числа виду
,
то досліджувати слід числа виду![]() і
і![]() ,
тобто числа
,
тобто числа![]() і
і![]() .
Де
.
Де![]() .
.
Знайдемо перший первісний корінь. Перевіряємо число 2.
![]() ,
,
![]() .
.
Оскільки 3<6, то 2 не є первісним коренем за модулем 7.
Тоді
![]() .
Отже, порядком числа 3 є 6, тобто 3 є
первісним коренем за модулем 7.
.
Отже, порядком числа 3 є 6, тобто 3 є
первісним коренем за модулем 7.
Другий
первісний корінь міститься серед чисел
виду
![]() , де (k,
m-1)=(k,
6)=1 і
1<k<6/
, де (k,
m-1)=(k,
6)=1 і
1<k<6/
Цій
умові задовільняє тільки число k=5.
отже, другим первісним коренем є число
![]() .
Оскільки
.
Оскільки![]() ,
то первісними коренями за модулем 7 є
числа 3 і 5.
,
то первісними коренями за модулем 7 є
числа 3 і 5.
Розв`язати конгруенцію
 .
(1)
.
(1)
Розв`язання.
Беремо індекси від обох частин конгруенції
![]() .
.
За таблицею індексів маємо:
![]() ;
;
![]() і тому
і тому
![]() ,
або
,
або
![]() (2)
(2)
Дістали лінійну конгруенцію відносно indx. Розв`яжемо її. Оскільки (18, 22)=2 і 4 ділиться на 2, то ця конгруенція має 2 розв`язки.
Скоротимо спочатку обидві частини і модуль на 2:
![]() .
.
До правої частини додамо число –11:
![]() .
.
Скоротимо обидві частини на 9:
![]() .
.
Дістаємо розв`язки конгруенції (2):
![]() ,
,
![]() .
.
За таблицею антиіндексів знаходимо відповідні два значення невідомого x:
![]() ,
,
![]() .
.
Знайти найменше натуральне число x, яке задовольняє наступну конгруенцію
 .
.
Розв`язання.
Індексуємо конгруенцію:
![]() .
.
За таблицями індексів:
![]() ;
;
![]() ,
одержуємо
,
одержуємо
![]() .
.
![]() ,
або
,
або
![]() приk=0,
1, 2, ..
приk=0,
1, 2, ..
Знайти остачу від ділення
 на 35.
на 35.
Розв`язання.
Скористаємося теоремами Ейлера і Ферма.
![]() ;
(13, 35)=(12, 35) = 1, тому
;
(13, 35)=(12, 35) = 1, тому
![]() .
.
Тоді
![]() .
.
Отже,
при діленні на 35 число
![]() дає остачу 11.
дає остачу 11.
