- •Программа
- •2. Место дисциплины (модуля) «Математика» в структуре ооп:
- •3. Требования к результатам освоения дисциплины (модуля) «Математика»:
- •4. Общий объем дисциплины (модуля) «Математика».
- •5. Содержание дисциплины (модуля) «Математика».
- •5.1. Содержание разделов дисциплины (модуля) «Математика»:
- •5.2 Разделы дисциплины и междисциплинарные связи с обеспечиваемыми (последующими) дисциплинами:
- •6.Учебно-методическое и информационное обеспечение дисциплины:
- •7. Материально-техническое обеспечение дисциплины:
- •8. Методические рекомендации по организации изучения дисциплины:
- •Раздел 7.Основы дифференциального исчисления (модуль):
- •Раздел 8. Неопределенный и определенный интегралы (модуль):
- •I курс:
- •II курс:
- •1 Курс.
- •II курс.
- •1, 2, 5
Если в параллелограмме, построенном на векторах
 и
и ,
, ,
то
,
тоПлощадь параллелограмма, построенного на векторах
 и
и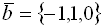 ,
равна
,
равна кв.ед.
кв.ед.1 кв.ед.
9 кв.ед.
27 кв.ед
Расстояние d от точки М0(3, 1) до прямой 4х+3у-10 = 0 равно
d = 2
d = 1
d = 3
d = 5
Уравнение
 на плоскости определяет
на плоскости определяетгиперболу с центром С (2, 0)
эллипс с центром С (0, 0)
окружность с центром С (2, 0)
гиперболу с центром С (0, 2)
Определитель матрицы
 равен
равен7
12
0
-6
Отношение модулей векторных произведений
 при
при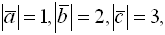
 равно
равно1
1/3
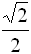
0
Даны два вектора
 и
и .
Скалярный квадрат вектора
.
Скалярный квадрат вектора равен
равен6
0
40
4
Даны два вектора
 и
и .
Острый угол
.
Острый угол между этими векторами равен
между этими векторами равен60°
45°
30°
90°
Векторы
 и
и коллинеарны при
коллинеарны при равно
равно-2
2
при всех


Даны два вектора
 и
и .
Вектор (
.
Вектор ( )
длиннее вектора (
)
длиннее вектора ( )
в k раз, где k равно
)
в k раз, где k равно2
1
5
3
Прямые
 и
и перпендикулярны, если число
перпендикулярны, если число равно
равно0
ни при каких

-1
1
Уравнение прямой, проходящей через точки М(1, 2) и N(0, 3), имеет вид
у = -х+3
у = х+1
х-у-3 = 0
х+у+3 = 0
Даны уравнения кривых:






 .
.
Дано уравнение эллипса
 .
Расстояния между вершинами эллипса
равны
.
Расстояния между вершинами эллипса
равныМатрицы А и В соответственно равны
 и
и .
Если det A =
.
Если det A = ,
то det В равен
,
то det В равен0
2

3


Матрица А равна
 .
Ее определитель det A равен
.
Ее определитель det A равен2
8 det A
0
2 det A
Длина вектора
 ,
если А (0,3,-2), В (4,-1,0) равна
,
если А (0,3,-2), В (4,-1,0) равна2
6
36
4
Даны векторы
 .
Вектору
.
Вектору ,
где точки А (2,4,8) и В (8,-8,2), коллинеарны
,
где точки А (2,4,8) и В (8,-8,2), коллинеарны и
и

ни один из векторов

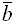
Отношение
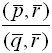 при
при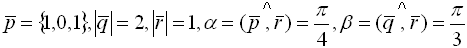 равно
равно

1

Даны векторы
 .
Вектору
.
Вектору ,
где точки А (2,4,8) и В (5,-2,5), коллинеарны
,
где точки А (2,4,8) и В (5,-2,5), коллинеарныни один из векторов

 и
и


Среди векторов
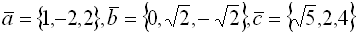 наименьшую длину имеет вектор
наименьшую длину имеет вектор


длины всех векторов равны
Проекция вектора
 на ось OZ равна
на ось OZ равна3
1
2
-1
Уравнение оси ОУ имеет вид
х = 0
х-у = 0
у+х = 0
у = 0
Расстояние между параллельными прямыми 4х+3у-1 = 0 и 4х+3у+4 = 0 равно
4
1
5
3
Из перечисленных прямых: 1) у =х; 2) 2у-х-1 = 0; 3) у = 2(х+1); 4) у = 1/2(x+1) через точки М1(1, 1) и М2(-1, 0), проходят прямые
1
3
2 и 4
1 и 2
Уравнение директрисы параболы
 имеет вид
имеет виду = 1
у+1 = 0
у = 2
у = 0
Уравнение биссектрисы I координатного угла в полярной системе имеет вид
Определитель
 равен
равен50
-20
0
-10
Определитель
 равен -1 при b равном
равен -1 при b равномb = 3
b = 0
b= -3
b = 1/3
Для определителя 3-го порядка
 и
и – cоответственно алгебраическое
дополнение и минор к элементу
– cоответственно алгебраическое
дополнение и минор к элементу , тогда разложение определителя по 2-й
строке имеет вид
, тогда разложение определителя по 2-й
строке имеет видМатрицы А и В равны соответственно
 ,
, .
Если det A =
.
Если det A = ,
то det В равен
,
то det В равен
15

0
2

Даны векторы
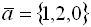 и
и .
Координаты их векторного произведения
.
Координаты их векторного произведения равны
равныОтношение
 при
при равно
равно0
2
1
-1/3
Уравнение прямой, проходящей через точку (1, 1) и перпендикулярной оси ОУ, имеет вид
х = у
у-1 = 0
х-1 = 0
х+у = 0
Прямые
 и
и параллельны,
если число
параллельны,
если число
 равно
равно1
4
-1

Фокусы эллипса имеют координаты
 и
и .
Большая полуось равна 5. Уравнение
эллипса имеет вид
.
Большая полуось равна 5. Уравнение
эллипса имеет видДлины векторов
 и
и ,
соответственно, равны 1 и 4, их скалярное
произведение равно 2. Угол между векторами
,
соответственно, равны 1 и 4, их скалярное
произведение равно 2. Угол между векторами ,
, равен
равенИз перечисленных прямых: 1) 2х-3у+1 = 0; 2) 6у-4х+2 = 0; 3) 3у = 4х-2; 4) 2х+3у-1=0; 5) 2х = 4+3у параллельными являются
1, 3, 5
1, 2, 4
1, 3, 4
1, 2, 5
На плоскости ХОУ каноническое уравнение оси ОУ имеет вид
х =у

х-у = 0
х+у = 0
Даны уравнения кривых второго порядка:
Уравнения асимптот гиперболы
 имеют вид
имеют видМатрица А равна
 .
Ее определитель det A равен
.
Ее определитель det A равен8 det A
0
2 det A
2
Определитель
 равен нулю при b равном
равен нулю при b равномb=1/2
b = -2
b = 2
b = 0
Числа
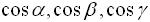 являются направляющими косинусами
вектора
являются направляющими косинусами
вектора .
Сумма их квадратов
.
Сумма их квадратов равна
равна41
7
1
1/7
Объем треугольной пирамиды с вершинами в точках А(0,0,0), В(2,1,1), С(0,1,1) и D(1,0,1) равен
1/3
0
1
2
Площадь треугольника АВС, где А(1,0,1), В(0,1,1), С(1,-1,1), равна
1 кв.ед.
1/4 кв.ед.
1/2 кв.ед.
2 кв.ед.
Прямые
 и
и перпендикулярны, если число
перпендикулярны, если число равно
равно-1/2
0
-1
-2
Прямые
 и
и параллельны, если число
параллельны, если число равно
равно-1

1
4
Уравнение прямой, проходящей через точки М1(1, 1) и М2(-5, -5), имеет вид
х-у+5 = 0
х-5 = 5-у
х = -у
х-у = 0
Уравнение окружности с центром в начале координат и с радиусом 3 в полярной системе имеет вид
Матрица А равна
 .
Ее определитель det A равен
.
Ее определитель det A равен2 det A
8 det A
2
0
Определитель
 равен нулю при b, равном
равен нулю при b, равномb =5/2
b = - 2/5
b = - 5/2
b = 0
Определитель матрицы
 равен
равен1
0
-12
12
Даны два вектора
 и
и .
Острый угол
.
Острый угол между этими векторами равен
между этими векторами равен90°
60°
30°
45°
Проекция вектора
 на ось OY равна
на ось OY равна2
1
-1
-2
Даны векторы
 .
Вектору
.
Вектору ,
где точки А (1,0,2) и В (2,1,3) ортогональны
векторы
,
где точки А (1,0,2) и В (2,1,3) ортогональны
векторы
 и
и

ни один из векторов

Векторы
 в порядке возрастания их модулей
расположены так:
в порядке возрастания их модулей
расположены так:Острый угол между прямыми 5х-у+7 = 0 и 2х -3у+1 = 0 равен
Прямая 2х+2у-3 = 0 образует с положительным направлением оси ОХ угол, равный

0


Дано уравнение кривой второго порядка
 .
Ее каноническое уравнение и тип кривой
.
Ее каноническое уравнение и тип кривой ,
эллипс
,
эллипс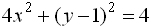 ,
окружность
,
окружность ,
гипербола
,
гипербола ,
гипербола
,
гипербола
Уравнение линии
 в декартовой системе имеет вид
в декартовой системе имеет вид