Раздел 8. Неопределенный и определенный интегралы (модуль):

Изучение понятий неопределенный и определенный интегралы связано с вычислением для данной функции первообразной: функция F(x) называется первообразной для функцииf(x) на заданном промежутке, если для всехxиз этого промежуткаF´(x)=f(x).

Например:

Функция есть первообразная для функциина интервале, так какдля всех.

Основное свойство первообразных (модуль) можно сформулировать так, что любая первообразная для функции f(x) на некотором промежутке [a;b] может быть записана в видеF(x)+c, гдеF(x) – одна из первообразных для функцииf(x) на промежутке [a;b], аc– произвольная постоянная.

1. Рассмотрим первообразные элементарных функций (модуль) в виде таблицы:

f(x)	F(x)	f(x)	F(x)
0	c
1	x+c	Sinx	–cosx+c
x
xn, n≠ –1		cosx	sinx+c
n · xn–1	xn+c

Если y=f(x) – непрерывная и неотрицательная функция на отрезке [a;b], аF(x) – её первообразная на этом отрезке, то площадьSсоответствующей криволинейной трапеции равна приращению первообразной на отрезке [a;b], т.е.S=F(b)–F(a).

Интегралом функции y=f(x) отaдоb, т.е.x[a;b] обозначают, т.е.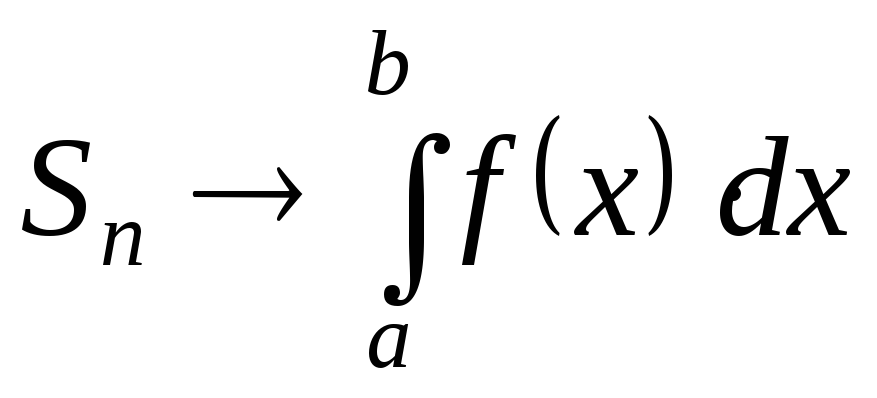приn∞ (читается как «интеграл отaдоbфункцииf(x) поdx).

Числа aиbназываются пределами интегрирования:

a– нижний предел;

b– верхний предел.

Знак ∫ называют знаком интеграла. Функция y=f(x) называется подинте-гральной функцией, а переменнаяx– переменной интегрирования. Если f(x)≥0 на отрезке [a;b], то площадьSсоответствующей криволинейной трапеции выражается формулой.

2. При вычислении определенных интегралов используется формула Ньютона-Лейбница:

,

S– площадь криволинейной трапеции;

– первообразные для функции на отрезке отaдоb;

f(x) – заданная функция;

aиb– пределы интегрирования;

x– переменная интегрирования.

Для удобства записи разность F(b)–F(a) (приращение функции на отрезке) принято сокращенно обозначать так:

Пользуясь этим обозначением, формулу Ньютона-Лейбница можно записать в виде:

Рассмотрим некоторые примеры вычисления определенных интегралов:

1)	Найдите площадь фигуры, ограниченной линиями y=cosx;;;y=0.

Решение.

Ответ:S=1.

2)	Найдите площадь фигуры, ограниченной линиями ;x=e; x=e2; y=0.

Решение.

.

Ответ: S=1.

3)	Найдите площадь фигуры, ограниченной линиями y=x2;x=1;x=2;y=0.

Решение.

Ответ: .

Контрольные работы:

I курс:

Контрольная работа 1.Тема 6.Матричная форма системы уравнений.

1. Вычислить определитель.

2. Найти матрицу обратную к матрице

.

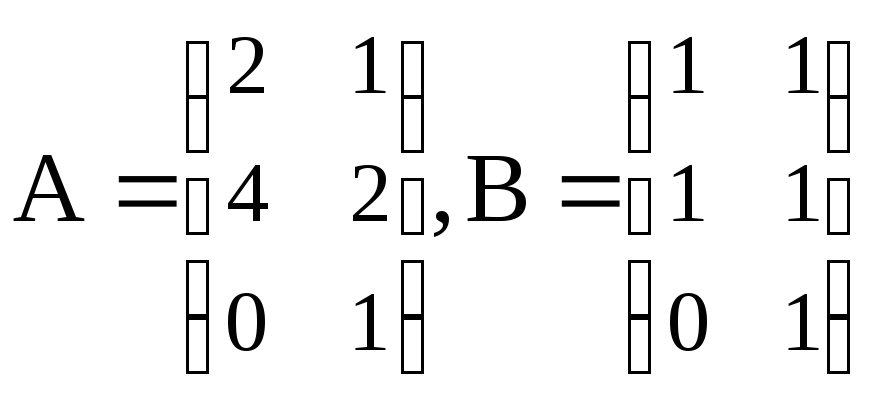3. Решить матричное уравнение

.

4. Решить систему уравнений с помощью обратной матрицы

5. Решить систему уравнений по формулам Крамера.

6. Решить систему уравнений методом Гаусса.

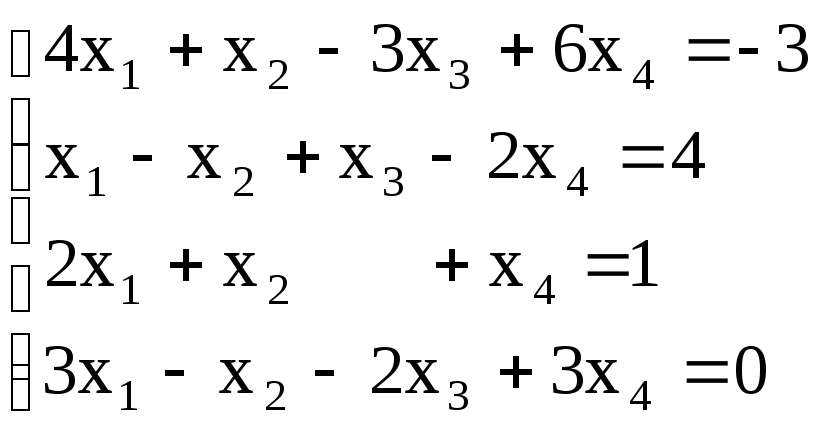
Контрольная работа 2.Тема 8.Линейная зависимость векторов.

1. Даны векторы .

Найти:

1) ,

2) ,

3) найти вектор , коллинеарный векторуи удовлетворяющий условию.

2. Даны векторы . Найти векторное произведение, синус угла между ними, площадь параллелограмма, построенного на этих векторах.

3. Вычислить произведение если

4. Найти точку пересечения прямой и плоскости 2x–y+z+1=0.

5. Составить уравнение плоскости, проходящей через точки М₁(2;3;-1) и М₂(1;5;3), перпендикулярно плоскости 3х – у +3z + 15 = 0.

6. При каких значениях C и D прямая лежит в плоскости 2x – y + Cz + D = 0?