
- •Российская академия народного хозяйства и государственной службы при президенте российской федерации
- •Литература
- •Указания к выполнению типового расчета
- •Раздел 1. Основные положения теории функций
- •Раздел 2. Приложение математического анализа функции одной переменной к задачам экономики и управления
- •2.1. Построение функций предложения и спроса
- •2.2. Определение равновесной цены и спроса (предложения) аналитическим методом
- •2.3. Определение эластичности спроса и предложения от цены
- •2.3. Экономическая интерпретация результатов математического анализа функции одной переменной
- •Задание на самостоятельную работу
2.2. Определение равновесной цены и спроса (предложения) аналитическим методом
Точка равновесия спроса и предложения может быть найдена аналитически путем совместного решения системы уравнений (2.1) и (2.2). Приравнивая эти две квадратичные функции, получаем уравнение второго порядка с одним неизвестным Q:
![]() ,
(2.19)
,
(2.19)
где постоянные а, b, c определяются по формулам:
![]() ;
;
![]() ;
;![]() .
(2.20)
.
(2.20)
Решением квадратного уравнения (2.19) будут два корня, определяемые по формуле
![]() ,
(2.21)
,
(2.21)
однако экономический смысл имеет только один из них, соответствующий положительному знаку перед радикалом, Qbal = 2,186. Эта величина и есть равновесный спрос (предложение).
Равновесная цена определится из уравнения (2.1) или (2.2):
![]() =
88.26; (2.22)
=
88.26; (2.22)
![]() =
88.26. (2.23)
=
88.26. (2.23)
На рис. 2.3 графически представлено решение уравнения (2.19).
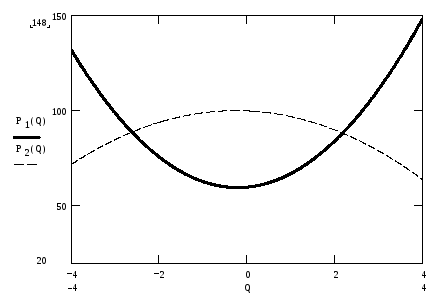
Рис. 2.3. Пересечение кривых спроса и предложения
Как видно из рис. 2.3, только одна точка пересечения парабол находится в области определения функций спроса и предложения.
2.3. Определение эластичности спроса и предложения от цены
Адекватным математическим понятием, характеризующим связь между изменением цены на реализуемую продукцию и объемом продаж, является эластичность спроса от цены ED. Она определяется как отношение
ED = – (Процентное изменение спроса) / (Процентное изменение цены). (2.24)
Исходя из определения (2.24), получаем рабочую формулу для расчета эластичности спроса от цены:
ED
= –
![]() ,
(2.25)
,
(2.25)
где Р и Q — соответственно цена и спрос; Р и Q — их абсолютные изменения. Часто располагают лишь двумя близкими значениями цены P1 и P2 и соответствующего им спроса. Тогда рассчитывают дуговую эластичность, которая, исходя из общей формулы (2.25), будет определяться как отношение
ED
= –
![]() ,
(2.26)
,
(2.26)
где Рср и Qср — соответственно средние цена и спрос; Р и Q — абсолютные изменения цены и спроса соответственно, рассчитываемые по простым формулам:
Рср = (P1 + P2)/2; Р = (P2 – P1);
Qср = (Q1 + Q2)/2; Q = (Q2 – Q1). (2.27)
Из теории дифференциального исчисления известно, что более адекватным понятием является так называемая точечная эластичность спроса от цены, определяемая по кривой спроса как
ED
= –
![]() ,
(2.28)
,
(2.28)
где
![]() —
скорость изменения спроса при изменении
цены.
—
скорость изменения спроса при изменении
цены.
Аналогично, эластичность предложения от цены ES определяется как отношение
ES = (Процентное изменение предложения) / (Процентное изменение цены). (2.29)
В отличии от формулы (2.24), здесь вместо знака () перед отношением стоит знак (+), поскольку предложение с ростом цены увеличивается (спрос, напротив, уменьшается).
По аналогии, точечная эластичность предложения от цены определяется по кривой предложения как
ES
=
![]() ,
(2.30)
,
(2.30)
где
![]() —
скорость изменения предложения при
изменении цены.
—
скорость изменения предложения при
изменении цены.
Располагая функциями спроса и предложения в виде квадратичных функций (2.1) и (2.2), можно рассчитать значения эластичности ED и ES в точке равновесия.
Так как мы
располагаем функциями спроса и предложения
в виде зависимости P
от Q,
то по ним можно рассчитать производные
![]() в точке равновесия:
в точке равновесия:
![]() 23,86;
(2.31)
23,86;
(2.31)
![]() 9,744.
(2.32)
9,744.
(2.32)
Обратные им
производные
![]() соответственно равны:
соответственно равны:
![]() 1/23.86
= 0.0419;
1/23.86
= 0.0419;
![]() 1/(9.744)
= 0.1026.
1/(9.744)
= 0.1026.
Подставляя в
формулы (2.28) и (2.30) значения производных
и равновесных Qbal
= 2.186 и
![]() =
88.26, получаем:
=
88.26, получаем:
ES
(Qbal)
=
![]() (88.26/2.186)*0.0419
= 1.69; (2.33)
(88.26/2.186)*0.0419
= 1.69; (2.33)
ED
(Qbal)
=
![]() (88.26/2.186)*(0.1026)
= 4.14. (2.34)
(88.26/2.186)*(0.1026)
= 4.14. (2.34)
Итак, в точке рыночного равновесия эластичность предложения по цене составляет 1,69. Эластичность спроса по цене в точке рыночного равновесия еще выше — 4,14.
