Раздел 2. Приложение математического анализа функции одной переменной к задачам экономики и управления

Рассмотрим следующую задачу.

Кривые предложения и спроса представлены квадратичными функциями (параболами):

, (2.1)

, (2.2)

где P — цена; Q — количество товара; a_s = 5; b_s = 2; c_s = 60; a_d = 2; b_d = 1; c_d = 100 — параметры, определенные эмпирически (индекс s относится к кривой предложения, индекс d — к кривой спроса).

Функции определены в области Q  [1, 4], однако для построения кривых область определения функций необходимо условно расширить до Q  [4, 4].

Необходимо:

1. построить кривые предложения и спроса;

2. найти равновесную цену и количество товара;

3. рассчитать точечную эластичность спроса и предложения от цены в равновесной точке.

4. дать экономическую интерпретацию полученным результатам.

2.1. Построение функций предложения и спроса

Так как обе функции — квадратичные вида

y = аx² + bx + с, (2.3)

где а, b, с — постоянные величины, то их графики представляют собой параболы с вершиной, находящейся в точке с координатами максимума или минимума.

Найдем координаты этих точек. Для функции предложения (2.1) имеем параболу

. (2.4)

Координаты стационарной точки (точки возможного экстремума) находим из условия равенства нулю первой производной:

. (2.5)

Отсюда абсцисса стационарной точки:

= –0,2. (2.6)

Подставив найденное значение в уравнения (2.1) и (2.4), находим ординату стационарной точки:

=60 – 0,2 = 59,8. (2.7)

Так как вторая производная функции (2.4) в стационарной точке М₀(,) больше нуля:

, (2.8)

то в этой точке будет минимум (имеет место “ускорение” функции, т. е. “скорость” ее роста в окрестности стационарной точке увеличивается, пройдя через нулевое значение).

Итак, мы получили координаты вершины (минимума) параболы, часть которой, отвечающая условию Q  [1, 4], описывает функцию предложения: М₀(=–0,2;=59,2).

Для построения кривой предложения необходимо иметь по крайней мере три точки. Вторую точку находим из условия равенства нулю (условно) абсциссы Q. Подставив Q = 0 в выражения (1) и (4), получаем:

= 60. (2.9)

откуда получаем координаты второй точки параболы М₁(Q = 0; Р = 60).

Координаты третьей точки М₂ находим из условия симметричности параболы относительно вертикальной прямой, проходящей через ее вершину. Абсцисса этой точки будет определяться по формуле

= –0,4, (2.10)

а ордината равна ординате точки М₁, т. е. М₂(Q = –0,4; Р = 60).

Эти три точки М₀, М₁ и М₂ полностью задают форму и расположение кривой предложения на графике. Но поскольку эти три точки расположены слишком близко друг к другу, для большей точности найдем координаты еще одной точки, отвечающей другой границе области определения функции предложения — Q = 4. Подставив в уравнение (2.4), получаем

= 148. (2.11)

Тем самым находим координаты четвертой точки М₃(Q = 4; Р = 148).

На рис. 2.1 показана кривая предложения, построенная по этим четырем точкам.

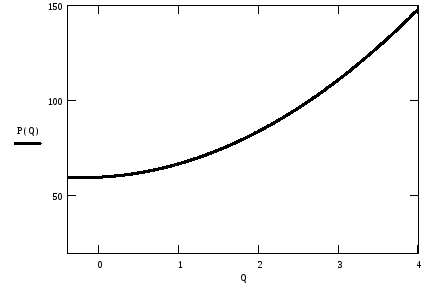
Рис. 2.1. Кривая предложения

Аналогично строим функцию спроса. Для функции спроса (2.2) имеем параболу

. (2.12)

Координаты стационарной точки (точки возможного экстремума) находим из условия равенства нулю первой производной:

. (2.13)

Отсюда абсцисса стационарной точки:

= –0,25. (2.14)

Подставив найденное значение в уравнения (2.2) и (2.12), находим ординату стационарной точки:

=100 + 0,125 = 100,125. (2.15)

Так как вторая производная функции (2.12) в стационарной точке М₀(,) больше нуля:

, (2.16)

то в этой точке будет максимум (имеет место отрицательное “ускорение” функции, т. е. “скорость” ее роста в окрестности стационарной точке уменьшается, пройдя через нулевое значение).

Итак, мы получили координаты вершины (максимума) параболы, часть которой, отвечающая условию Q  [1, 4], описывает функцию спроса: М₀(=–0,25;= 100,125).

Для построения кривой спроса также необходимо иметь по крайней мере три точки. Вторую точку находим из условия равенства нулю (условно) абсциссы Q. Подставив Q = 0 в выражения (2.2) и (2.12), получаем:

= 100. (2.17)

откуда получаем координаты второй точки параболы М₁(Q = 0; Р = 100).

Координаты третьей точки М₂ находим из условия симметричности параболы относительно вертикальной прямой, проходящей через ее вершину. Абсцисса этой точки будет определяться по формуле

= –0,5, (2.18)

а ордината равна ординате точки М₁, т. е. М₂(Q = –0,5; Р = 100).

Эти три точки М₀, М₁ и М₂ полностью задают форму и расположение кривой спроса на графике. Но поскольку эти три точки расположены слишком близко друг к другу, для большей точности найдем координаты еще одной точки, отвечающей другой границе области определения функции спроса — Q = 4. Подставив в уравнение (2.12), получаем

= 64. (2.19)

Тем самым находим координаты четвертой точки М₃(Q = 4; Р = 64).

На рис. 2.2 показана кривая спроса, построенная по этим четырем точкам.

Рис. 2.2. Кривая спроса