Задача 7.
Следующие комплексные числа изобразить векторами на комплексной плоскости и записать в тригонометрической и показательной форме:
Ответ:
;
Ответ:
;
Ответ: 
.
Задача 8.
Даны комплексные числа
,
и
.
Найти
.
Решение:
.
Задача 9.
Вычислить
в алгебраической, тригонометрической,
и показательной формах.
Решение:
,
,
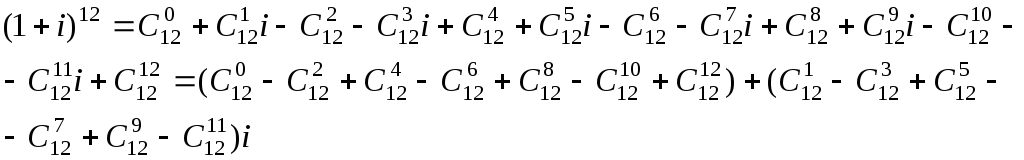
Задача 10.
Докажите, что:
Указание:
Результат предыдущей задачи обобщить
на случай
и сравнить алгебраические и
тригонометрические выражения для
действительной и мнимой частей.
Задача 11.
Найти
.
Решение:
;
;
;
;
.
Задача 12.
Найти корни уравнения
.
Решение:
Задача 13.
Зная, что
является одним из значений
,
записать все значения
.
Ответ:
.
Задача 14.
Доказать формулы Эйлера:
Задача 15.
Найти
,
,
и
,
если
,
а
.
Ответ:
,
,
и
.
Задача 16.
Решить уравнения:
|
|
Ответ: |
|
|
|
Ответ: |
|
Задача 17.
Пусть
,
при котором
.
Найти:
,
,
,
,
.
Определить тип отображения
.
Ответ:
;
;
;
;
.
Отображение
не инъективное и не сюръективное.
Задача 18.
Пользуясь
формулой Муавра, доказать справедливость
выражения:
.
Указание:
Использовать формулу
.
Задача 19.
Пользуясь формулой Муавра, выразить
через
и
.
Ответ:
.
Задача 20.
Используя формулы Эйлера, найти суммы:
|
|
Ответ: |
|
|
|
Ответ: |
|
Практическое занятие 3. Векторы
Вопросы для повторения
Модуль вектора, формула расстояния между двумя точками.
Понятие коллинеарности векторов.
Понятие компланарности векторов.
Понятие проекции вектора на ось.
Линейные операции над векторами.
Скалярное произведение векторов.
Векторное произведение векторов.
Смешанное произведение векторов.
Векторы называются коллинеарными, если они расположены на одной или на параллельных прямых, икомпланарными, если они лежат на одной или на параллельных плоскостях.
Вектор, длина которого равна единице,
называется единичным вектором илиортом. Орт обозначатся
.
Длина вектора
,
заданного координатами своих концов,
т.е. расстояние между точками
и
вычисляется по формуле:
.
Скалярными произведением
двух векторов
и
называется число, равное произведению
их длин на косинус угла между ними:
.
Если векторы заданы своими координатами
и
,
т.е.
,
,
то, перемножая эти векторы скалярно и
используя таблицу умножения ортов,
получим выражение скалярного произведения
через координаты векторов:
.
Задача 21.
Даны координаты двух точек
и
.
Найти координаты вектора
и его длину.
Решение:
Координаты вектора:
Длина вектора
.
Задача 22.
Даны две точки
и
.
Найти координаты вектора
.
Решение:
.
Задача 23.
Найти длину вектора
и его направляющие косинусы.
Решение:
.
;
;
.
Задача 24.
Определить, при каких
и
векторы
и
коллинеарны.
Ответ: 
.
Задача 25.
Даны три вершины параллелограмма
:
;
;
.
Найти его четвертую вершину
.
Ответ: 
.
Задача 26.
Векторы
и
образуют угол
,
причем
,
.
Определить
и
.
Ответ: 
.
Задача 27.
Найти координаты и длину вектора
,
если
,
,
.
Ответ: 
.
Задача 28.
Дан вектор
,
образующий с осью
угол
,
и вектор
,
образующий с той же осью угол
.
Найти проекцию суммы
,
где
,
на ось
,
если известно, что
,
.
Решение:
Так как проекция суммы векторов равна
сумме их проекций, необходимо найти
проекцию каждого слагаемого на ось
.
;
;
.
Задача 29.
Разложить вектор
по векторам
и
.
Решение:
;
;
;
.
.
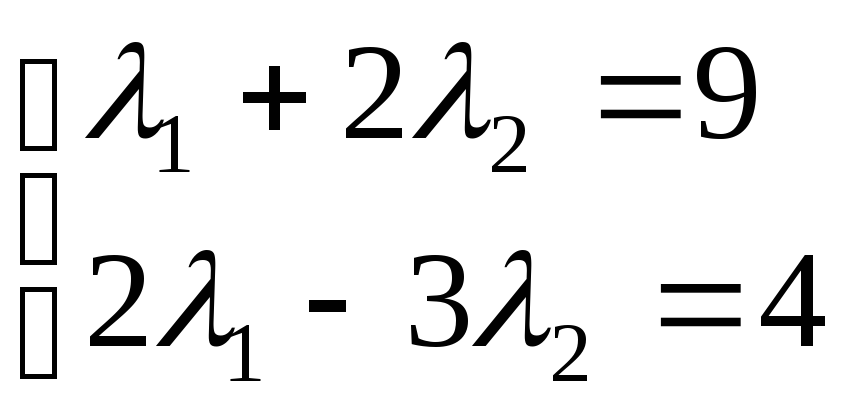
Задача 30.
Найти проекцию вектора
на ось, составляющую с координатными
осями равные острые углы.
Ответ: 
.
Задача 31.
Найти проекцию вектора
на вектор
.
Ответ: 
.
Задача 32.
Даны вершины четырехугольника
;
;
;
.
Доказать, что его диагонали взаимно
перпендикулярны.
Решение:
;
;
.
Задача 33.
Некоторая фирма продает изделия в шести
регионах по ценам, которые характеризуются
вектором
,
а вектор
характеризует объемы продаж по регионам.
Найти объем реализации изделий.
Решение:
.
Задача 34.
Фирма продает изделия в четырех регионах
по ценам, которые характеризуются
вектором
,
а вектор
характеризует объемы продаж по регионам.
Найти прибыль от реализации изделий,
если издержки составляют 2000 денежных
единиц.
Решение:
Практическое занятие 4. Векторное и смешанное произведения векторов
Вопросы для повторения
Векторное произведение векторов.
Смешанное произведение векторов.
Определитель матрицы третьего порядка вычисляется следующим образом:
Метод Саррюса
Определитель матрицы третьего порядка представляет собой алгебраическую сумму шести слагаемых. Каждое слагаемое является произведением трех элементов, расположенных в разных столбцах и разных строках матрицы.
Знак «плюс» имеют произведение элементов, образующих треугольники со стороной, параллельной главной диагонали.
Знак «минус» имеют произведение элементов, принадлежащих побочной диагонали, и два произведения элементов, образующих треугольники со стороной, параллельной побочной диагонали.
С помощью формул разложения определителя матрицы по элементам строки или столбца вычисление определителя матрицы любого порядка сводится к вычислению определителей матриц второго или третьего порядков.
Векторным произведениемвектора
на вектор
называется вектор
,
длина и направление которого определяется
условиями:
,
где
‑ угол между
и
;
перпендикулярен каждому из векторов
и
;
направлен так, что кратчайший поворот
от
к
виден
из его конца совершающимся против
часовой стрелки.
В матричной форме формулу вычисления векторного произведения векторов можно записать в виде:
.
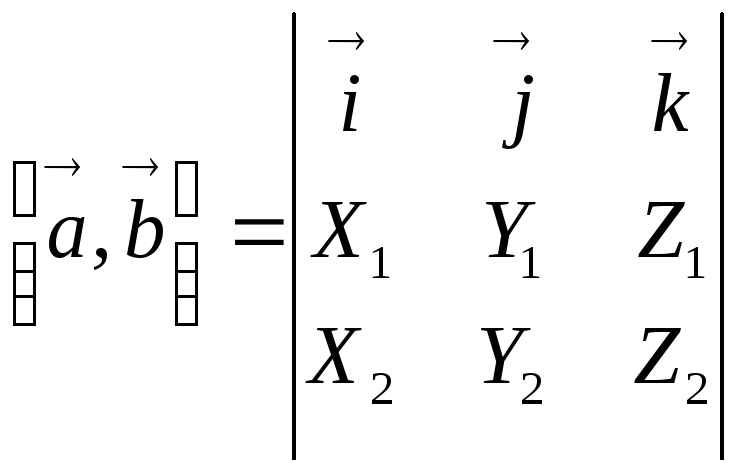Смешанным произведениемтройки
векторов
,
и
называется число, равное скалярному
произведению вектора
на векторное произведение
.
Если
,
и
то:
,
или в свернутой форме:
.