II Параметрическое задание пути интегрирования

Теорема 2. Пусть путь задан уравнениями

причем функции и– непрерывно-дифференцируемы ии. Пусть, кроме того, проекции вектор-функции– непрерывны вдоль. Тогда криволинейный интеграл 2^го рода существует и вычисляется по формуле

(2)

Замечание 2. Формула (2) легко обобщается на трёхмерный случай.

Замечание 3. Формула (2) остаётся верной и для замкнутых путей интегрирования, если только направление обхода пути совпадает с естественным изменением параметра.

Пример 2. Вычислить где

(L) – петля линии ,.

Решение. При естественном изменении параметра (от до) петля линии соответствует значениями пробегается по часовой стрелке, т. е. в отрицательном направлении. Поэтому:

§6. Формула Грина

Эта формула устанавливает связь между интегралами двух типов: криволинейным и двойным. Она широко применяется как в самом анализе, так и в его приложениях.

Теорема. Пусть – правильная ограниченная область вс гладкой или кусочно-гладкой границей, а функцииинепрерывны ввместе со своими производнымии. Тогда имеет место формула:

которую называют формулой Грина.

Доказательство. Докажем отдельно, что

(1)

(2)

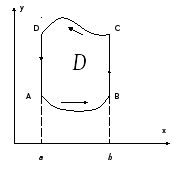Пусть область является правильной в направлении осиОх:

Граница области состоит из гра- -фиков двух функций

,

и отрезков двух прямых, параллельных оси (эти отрезки могут вырождаться в отдельные точки). Поэтому

Формула (1) доказана.

Для доказательства формулы (2) считаем, что область имеет видИмеем для левой части формулы(2):

В предпоследнем равенстве применили формулу Ньютона – Лейбница, прочитав её слева направо. Итак, формула (2), а с ней и формула Грина, доказана.

Пример 1. Найти

Решение. Предварительные вычисления:

Используя формулу Грина, заменяем криволинейный интеграл по окружности двойным интегралом по кругу:

Замечание. Формула Грина позволяет вывести удобную формулу для вычисления площади плоской фигуры с помощью криволинейного интеграла 2^го рода.

Пусть . Тогда Отсюда получим для площади области

где – граница области . Подынтегральное выражение записывают в форме определителя:

Пример 2. Площадь эллипса

Пример 3. В примере 2, §5 мы нашли интеграл где – петля линии . Тем самым мы нашли площадь фигуры, ограниченной этой петлёй:

§7. Независимость криволинейного интеграла 2го рода от формы пути интегрирования

В общем случае криволинейный интеграл 2^го рода зависит не только от начальной и конечной точек, но и от формы пути интегрирования. Однако, существуют условия, когда этой зависимости нет. Точная формулировка:

говорят, что интеграл не зависит от формы пути интегрирования (кратко “от пути”) в области , если для любых точек А и В из этой области, значения этого интеграла по любой линии остаётся одним и тем же.

Для такого случая используется обозначение

Прежде чем формулировать основной результат докажем две леммы.

Лемма 1. Криволинейный интеграл не зависит от пути в области тогда и только тогда, когда интеграл по любому контуру .

Доказательство.

Лемма 2. Если криволинейный интеграл не зависит от пути в области , причём функции и непрерывны в , то выражение является полным дифференциалом некоторой функции.

Доказательство. Если интеграл не зависит от пути и точка фиксирована, то этот интеграл будет функцией координат точки :

Вычислим по определению частную производную . Для этого сначала найдём частное приращение этой функции:

Здесь: . При этом пусть причём т.е. уравнение этого части пути интегрирования . Напомним, что по условию интеграл не зависит от пути, поэтому путь мы выбираем удобным для нас. Используя свойства криволинейного интеграла, получим:

.

Применяя к последнему интегралу теорему о среднем, получим окончательно:

Теперь можно вычислить искомую производную:

Аналогично можно доказать, что . Таким образом имеем:

что и требовалось доказать.

Теперь мы можем сформулировать и доказать основную теорему, дающую условия независимости криволинейного интеграла 2^го рода от пути.

Теорема. Пусть функции непрерывны в ограниченной правильной области . Тогда для независимости интеграла от пути необходимо и достаточно, чтобы в области выполнялось условие

Доказательство. Необходимость. Если интеграл не зависит от пути, то в силу леммы 2 существует функция такая, что и . Теперь остаётся вспомнить теорему о равенстве смешанных производных:

Достаточность. Если , то в силу формулы Грина имеем

т.е. интеграл по любому замкнутому контуру равен нулю. В силу леммы 1 это означает, что интеграл не зависит от пути.

Пример 1. Проверить независимость от пути для интеграла

и вычислить его, если .

Решение. Выпишем функции и , и вычислим их частные производные:

Легко видеть, что все условия теоремы выполняются в любой ограниченной правильной области , не содержащей точек оси , следовательно, интеграл не зависит от пути в такой области. Данные точки А и В можно погрузить в такую область. Поэтому

.

В качестве пути мы выбрали ломанную, звенья которой параллельны осям координат. Уравнения этих звеньев:

Итак, криволинейный интеграл сводится к сумме двух определённых: