Лабораторная работа №8 Синтез дискретных фильтров средствами matlab.

Цель работы: приобретение практических навыков проектирования дискретных фильтров заданных параметров с использованием функций и графических средств MATLAB.

Общие сведения:

В MATLAB имееться 26 функций синтеза дискретных фильтров, которые сосредоточены в следующих пакетах:

• Signal Processing (SP) – 18 функций

• Communications (Comm) – 3 функции

• Filter Design (FD) – 5 функций

В пакете SP имееться программа FDA Tool (Filter Design and Analysis Tool), реализующая графический интерфейс для расчета фильтров и просмотра их характеристик.

Рассмотрим некоторые из функций и особенности их использования при синтезе дискретных фильтров.

Все функции подразделяються в соответствии с типом синтезируемого фильтра(рекурсивный или нерекурсивный) и принятым для этого методом синтеза. В соответствии с этим можно выделить следующие группы функций для синтеза рекурсивных фильтров:

• Билинейного Z-преобразования

• Инвареантного преобразования импульсных характеристик

• Субоптимального метода синтеза

• Оптимального синтеза

Для синтеза нерекурсивных фильтров можновыделить следующие функции:

• Субоптимального метода синтеза

• Оптимальные методы синтеза

1.Функции синтеза рекурсивных фильтров.

1.1.Функции синтеза стандартных фильтров методом билинейного

Z-приобразования.

В пакете SP имеются готовые функции расчета дискретных фильтров: Баттерворта, Чебышева первого и второго рода и эллептических (Кауэра). Эти функции позволяют выполнить расчет дискретных ФНЧ, ФВЧ, полосовых и режекторных фильтров по аналоговым прототипам методом билинейного Z-приобразования фильтров, только без последнего параметра «S», кроме того, частоты среды задаються нормированными к частоте Найквиста. Аналогично для дискретных фильтров используються те же функции, и для выбора минимального порядка фильтра что и дляаналоговых фильтров.

Можно рекомендовать следующую последовательность расчета рекуррентных дискретных фильтров методом билинейного Z-преобразования с использованием аналогового прототипа:

А) используя функции:

• [n,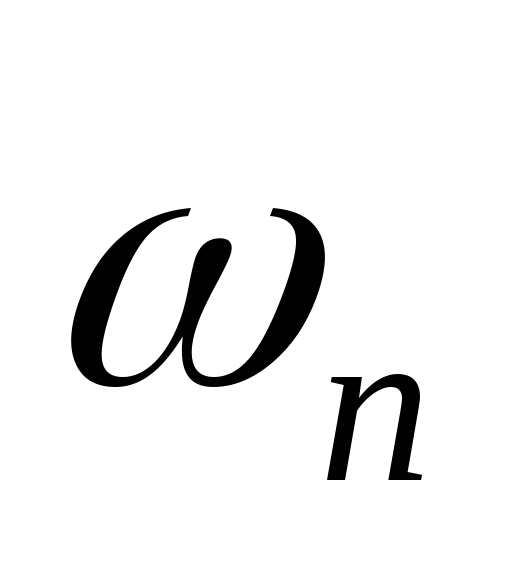] = buttord(,,,);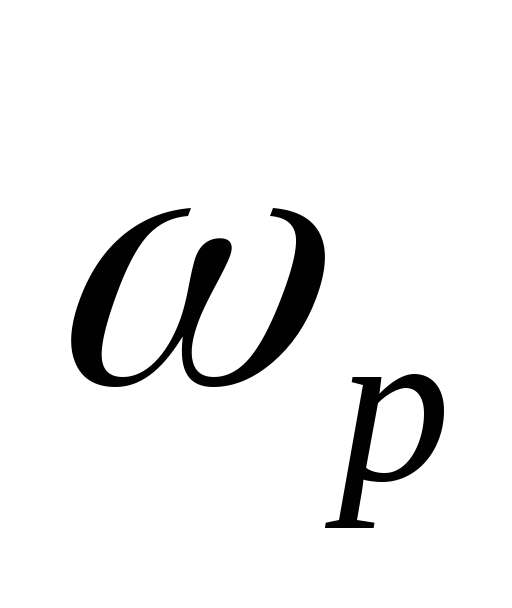

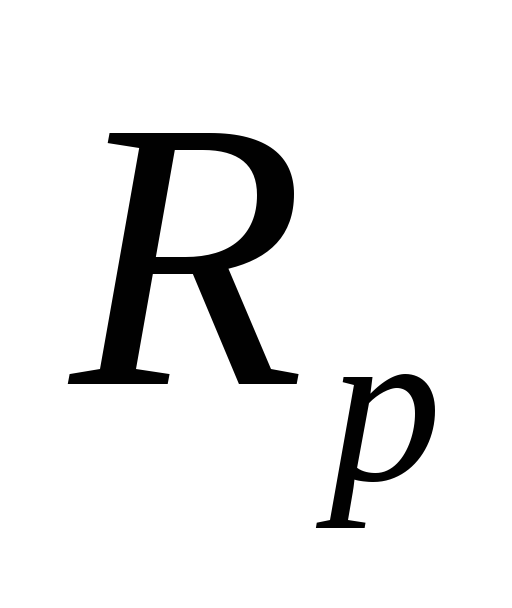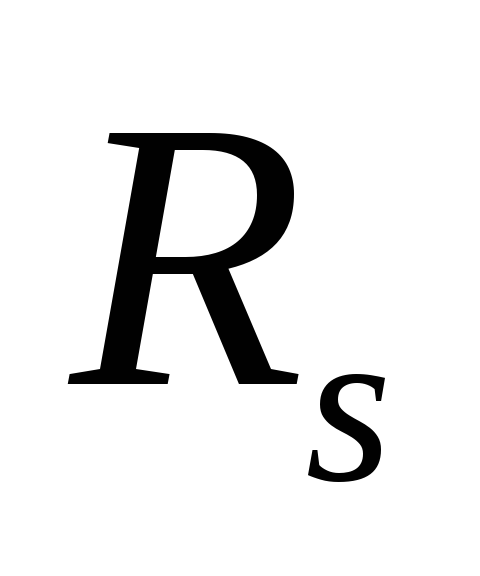• [n,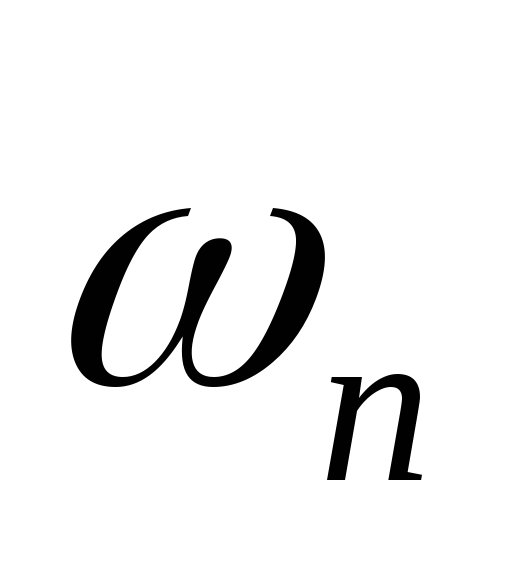] = cheb1ord(,,,);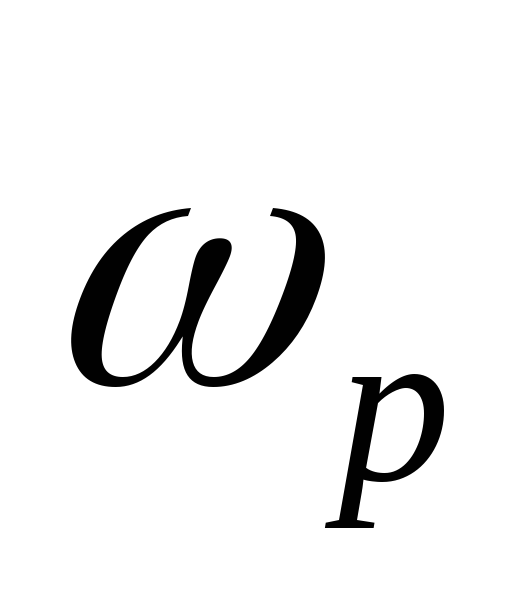

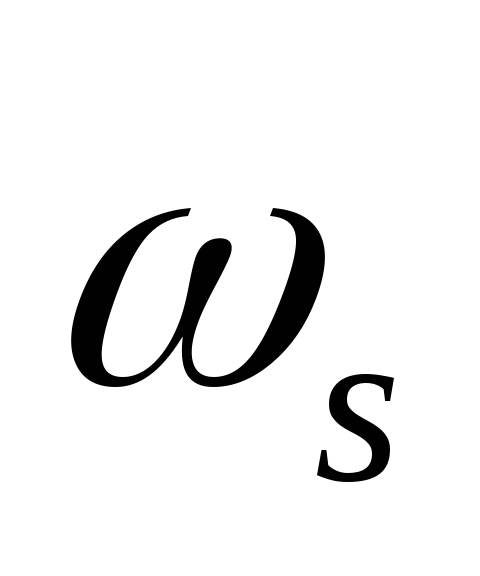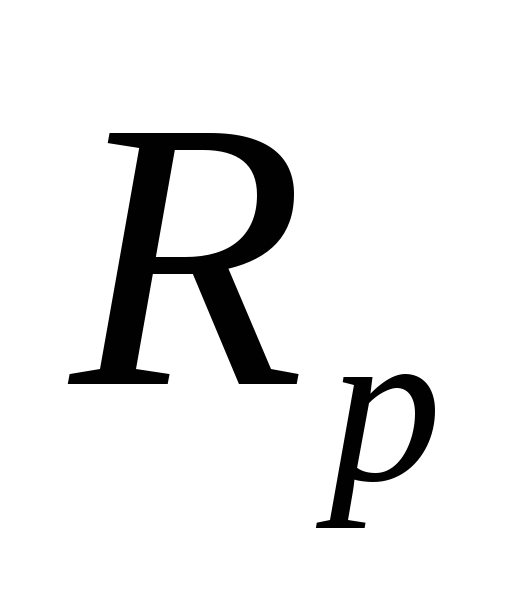• [n,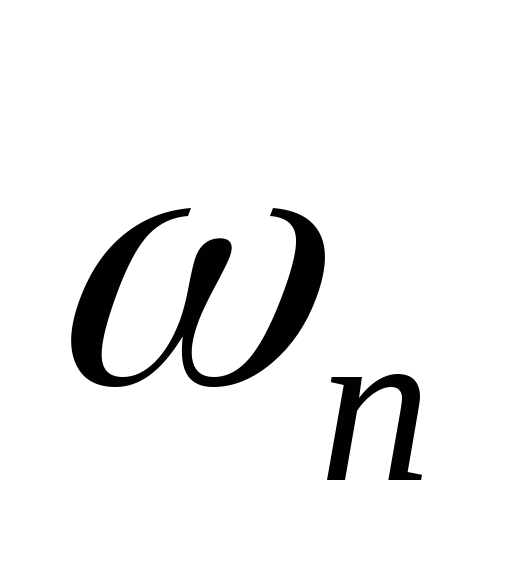] = cheb2ord(,,,);

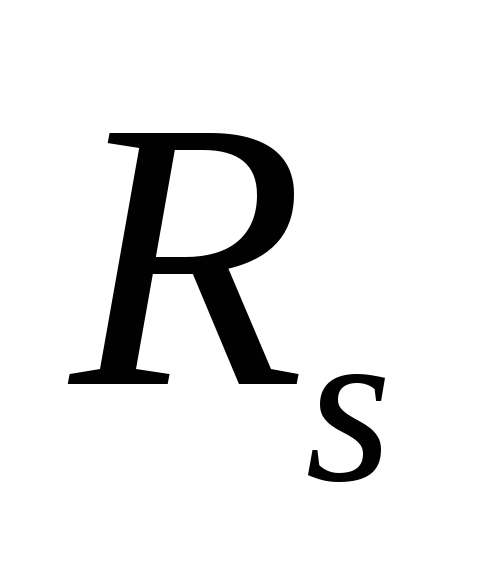• [n,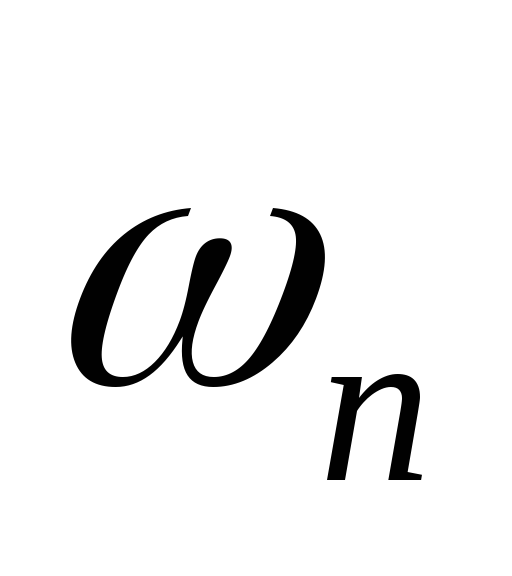] = ellipord(,,,)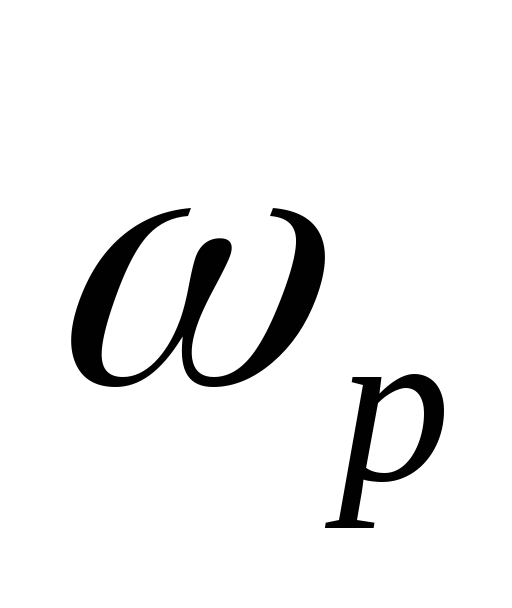

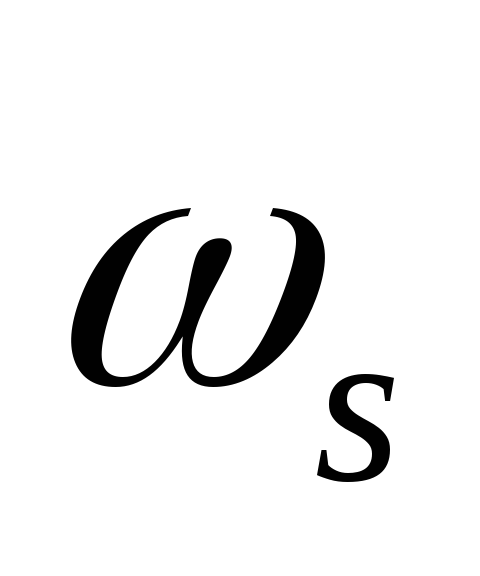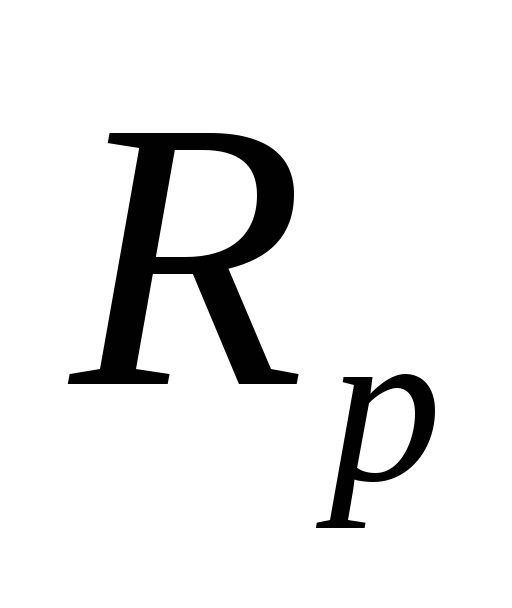Рассчитывают минимальный порядок фильтра; и - в децибелах;

, частоты нормированные в частоте Наквиста. Назначение параметров и способы задания см. лабораторную работу №5 «Исследование характеристик и параметров аналоговых фильтров».

Б) рассчитывают требуемый тип фильтра, используя следующие функции MATLAB:

• butter(n,,tupe) – расчет фильтров Баттерта;

• cheby1(n,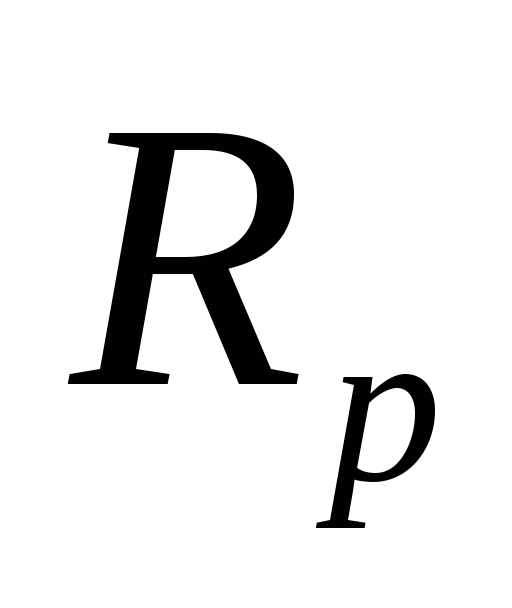,,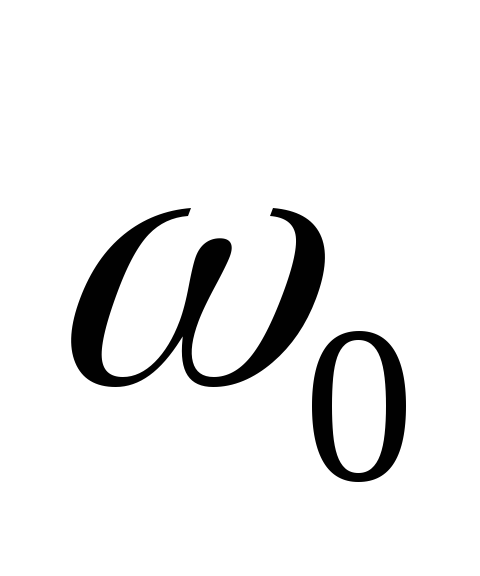tupe) – расчет фильтров Чебышева первого рода;

• cheby2(n,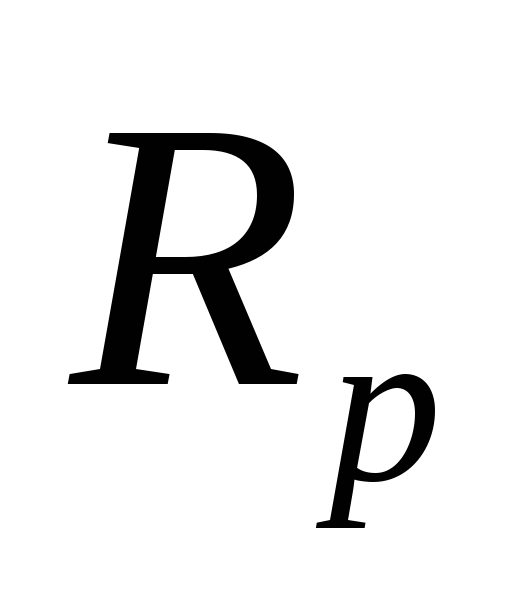,,tupe) – расчет фильтров Чебышева второго рода;

• ellip(n,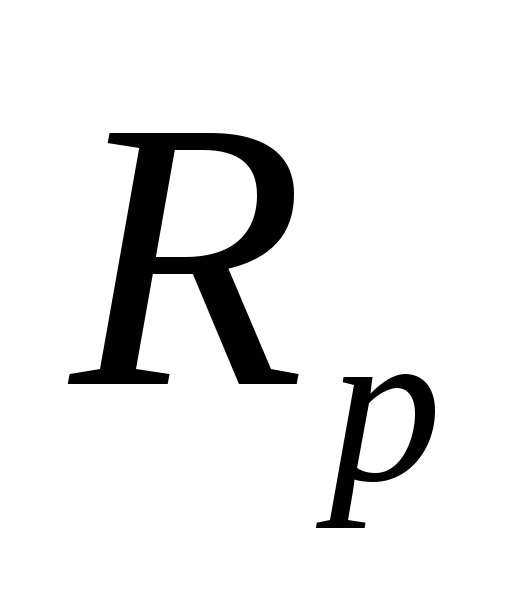,,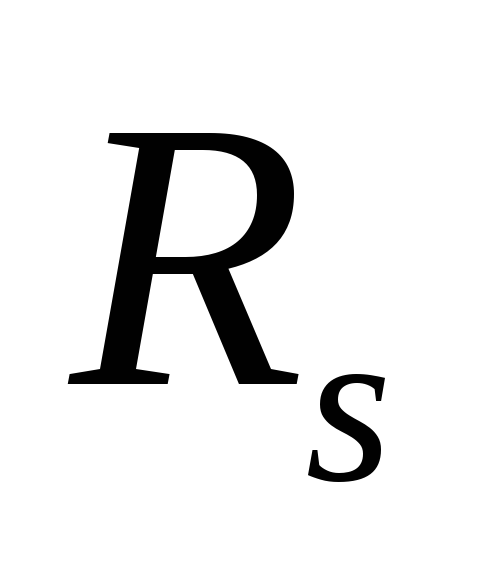,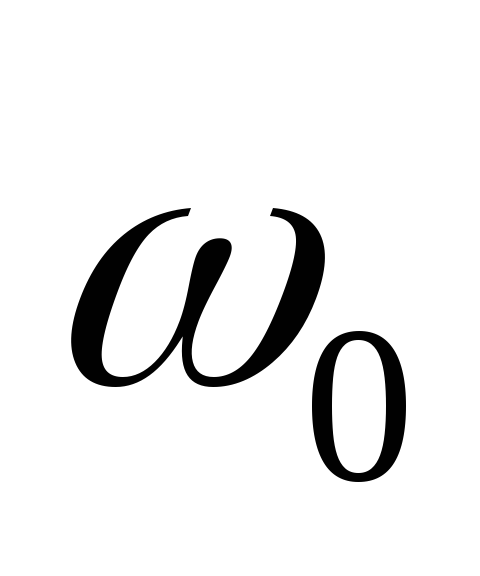tupe)– расчет фильтров Кауэра(эллиптических).

Параметры всех функций задаються одинаково, их назначение и способы задания, такие же как и при расчете аналоговых фильтров. Отличие – отсутсвие строк «S», а частота среза - нормирована к частоте Найквиста.

В зависимости от количества параметров указанных при вызове, функции могут возвращать результаты расчетов в виде коэффициентов полиномов числителя и знаменателя функции передачи (два выходных параметра), нулей и полюсов (три выходных параметра) либо параметров пространства состояний (четыре выходных параметра):

[a,b]= ...

[Z,P,K]= ...

[A,B,C,D]= ...