Задачі кореляційно-регресійного аналізу:

1. Встановлення форми зв'язку між змінними і отримання рівняння регресії в явному вигляді.

2. Оцінка тісноти зв'язку між змінними.

Приклад

Таблиця 2.1 – Масив експериментально одержаних даних

X	1,0	1,5	3,0	4,5	5,0
У	1,25	1,4	1,5	1,75	2,25

Кореляційне поле (точковий графік) – це графічне зображення сукупності експериментально одержаних даних у вигляді крапок в системі координат.

Якщо з'єднати всі крапки у порядку зростання Х відрізками прямої одержимо емпіричну (спостережувану) лінію регресії.

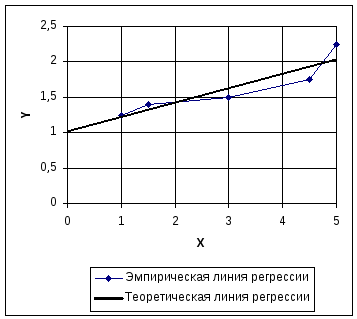
Рис.2.9. Кореляційне поле, емпірична і теоретична лінії регресії

Рівняння лінійної регресії:

,

де - параметри рівняння регресії.

Лінія регресії, побудована по рівнянню регресії, називається теоретичною лінією регресії.

МЕТОД ЯКНАЙМЕНШИХ КВАДРАТІВ (МНК)

Відповідно до ідеї :

,

де - значення змінних в i-той точці (спостережувані в експерименті значення);

- теоретичні (розрахункові) значення У при спостережуваних в експерименті значеннях ;

n - кількість експериментально одержаних точок.

;

.

;

.

• коефіцієнт регресії

;

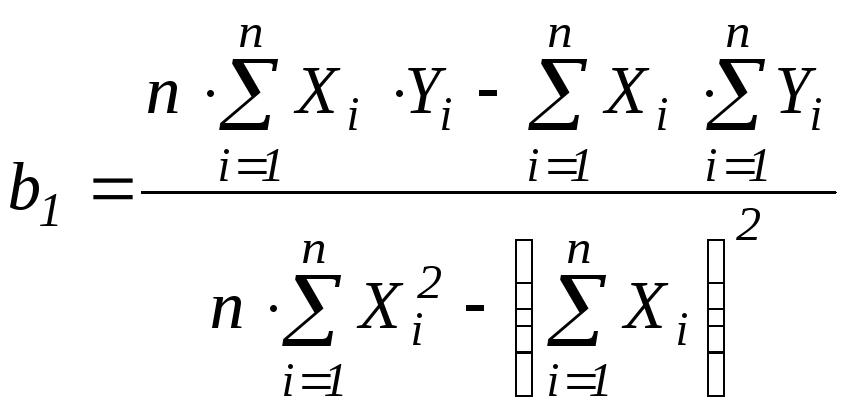• вільний член

,

де

- середні значення відповідно X і У для даного масиву експериментальних даних.

Таблиця 2.2 - Дані для розрахунку параметрів рівняння регресії

i		X		У
1 2 3 4 5	1,0 1,5 3,0 4,5 5,0		1,25 1,40 1,50 1,75 2,25		1,00 2,25 9,00 20,25 25,00		1,250 2,100 4,500 7,875 11,250			1,5625 1,9600 2,2500 3,0625 5,0625
∑	15,0		8,15		57,50		26,975			13,8975
∑/5	3,0		1,63		11,50		5,395			2,7795

;

.

.

Оцінка «тісноти» зв'язку між змінними

Для кількісної оцінки «тісноти» і напряму лінійного зв'язку між змінними використовується коефіцієнт кореляції:

;

.

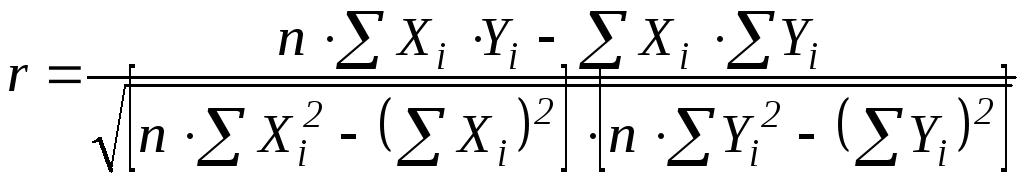Діапазон зміни коефіцієнта кореляції: .

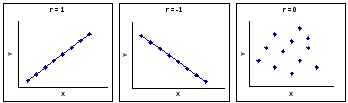
Рис.2.10. Граничні значення коефіцієнта кореляції

- зв'язок дуже слабкий;

- зв'язок сильний;

- зв'язок є.

Для оцінки «тісноти» зв'язку при будь-якій формі зв'язку використовується кореляційне відношення:

,

де R² - коефіцієнт детермінації.

Діапазон зміни: .

,

де

- міжгрупова дисперсія (дисперсія чинника, що відображає вплив тільки врахованих чинників (Х) на той, що коливається, результат (Y);

- загальна дисперсія, що відображає вплив всіх чинників (як врахованих, так і не врахованих) на той, що коливається, результат (Y).

Дисперсія характеризує розсіювання (ступінь «розкиду») випадкової величини навколо її математичного очікування (середнього значення).

,

де

- залишкова дисперсія, що оцінює той, що коливається результату У під впливом всіх неврахованих чинників.

Загальна дисперсія

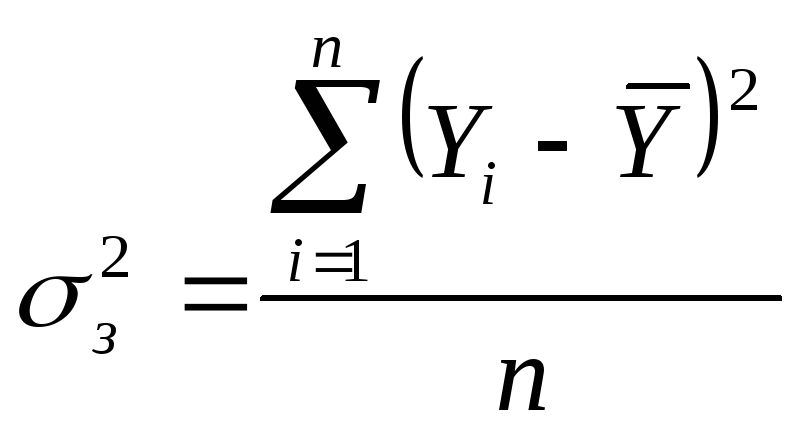. (2.1)

Міжгрупова дисперсія

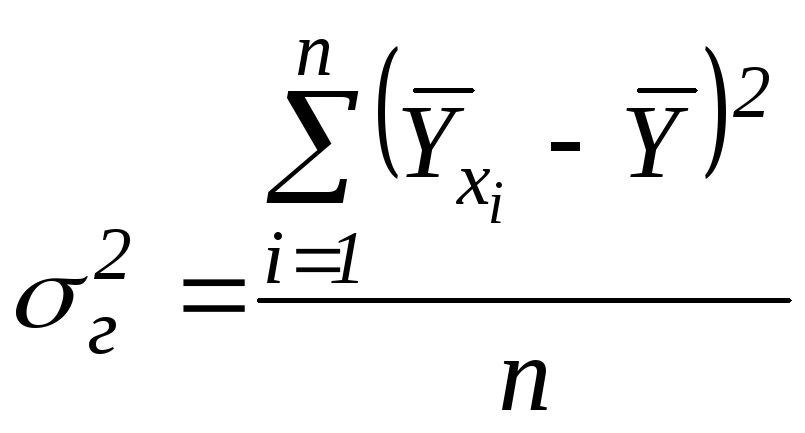. (2.2)

Залишкова дисперсія

. (2.3)

- фактично набуті в експерименті значення У при спостережуваних значеннях ;

- розрахункові (по оціненому аналітичному рівнянню регресії) значення У при спостережуваних значеннях ;

- середнє значення У для даного масиву експериментально одержаних даних,

Рис.2.11. До питання визначення загальної, міжгрупової і залишкової дисперсії

Таблиця 2.3 – Дані для розрахунку дисперсії

i
1	0,1444	0,16322	0,00058
2	0,0529	0,09181	0,00533
3	0,0169	0,00000	0,01690
4	0,0144	0,09181	0,03349
5	0,3844	0,16321	0,04665
Σ	0,6130	0,51005	0,10295

.