Лекция № 23.

Пример 1. Исследовать и построить график функции .

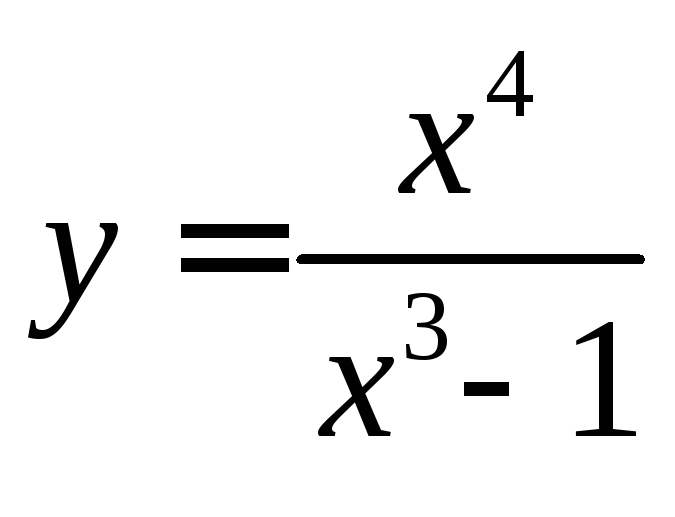1. .

2. Функция общего вида.

3.

4. Функция, как элементарная, непрерывна всюду, кроме .

Вычислим односторонние пределы:

.

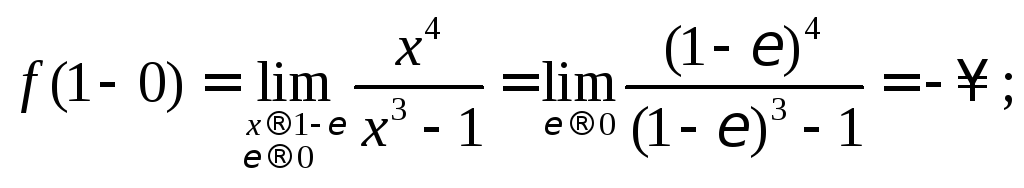
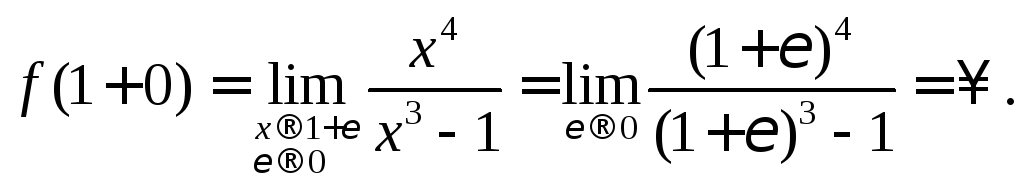Таким образом, точка является точкой разрыва второго рода.

5. Вычислим производную

.

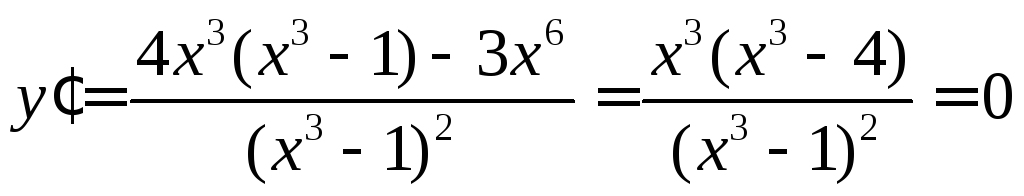Находим критические точки: .

Построим таблицу

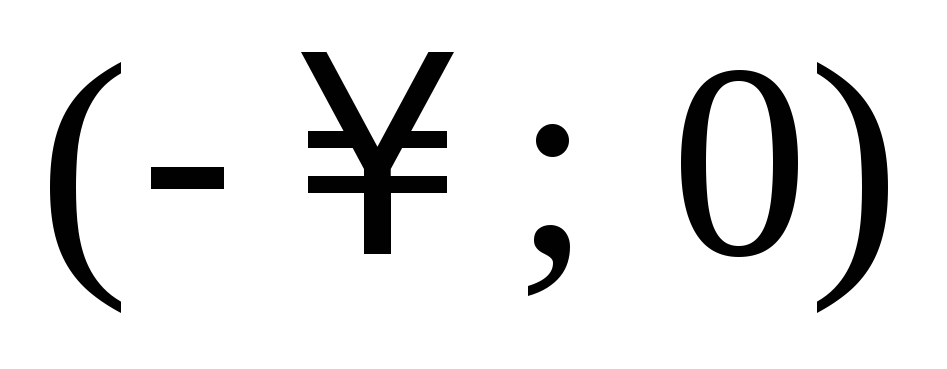
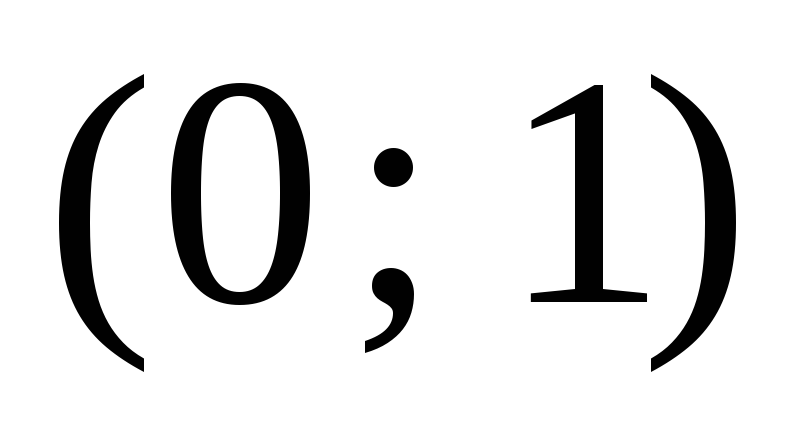
х		0		1
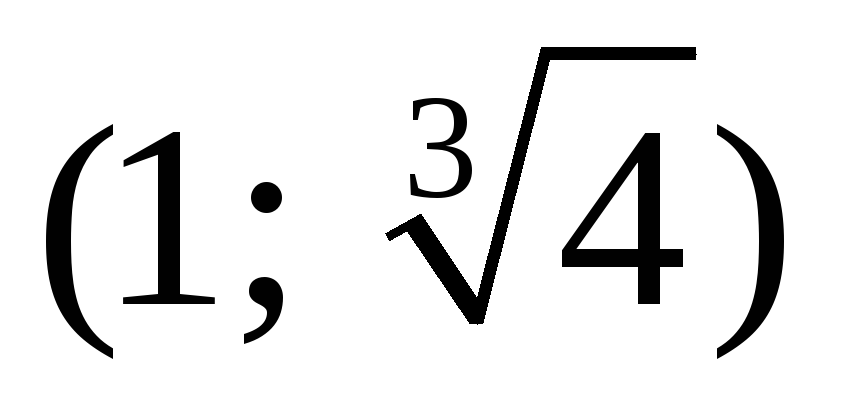
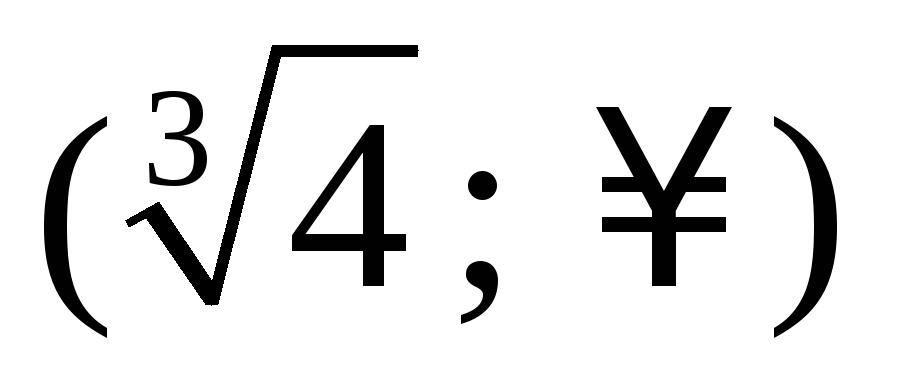
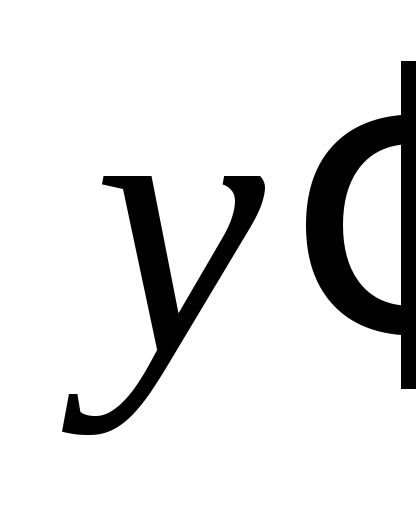
	+	0				0	+
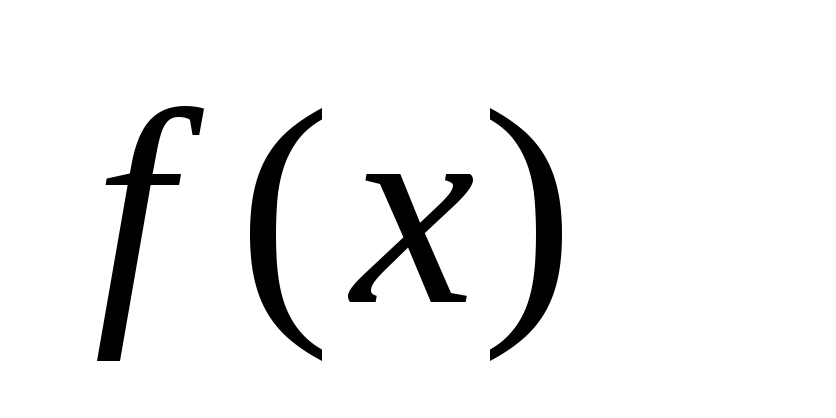
у		0

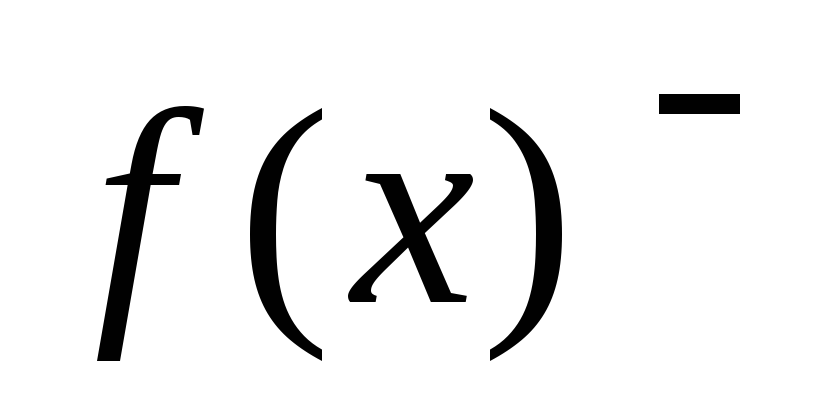
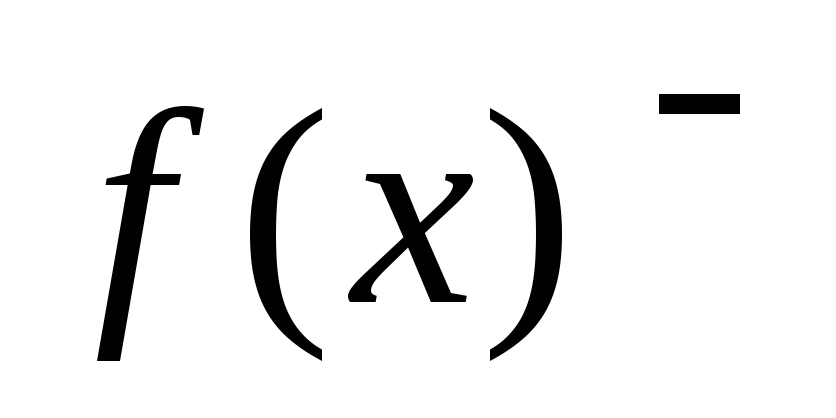
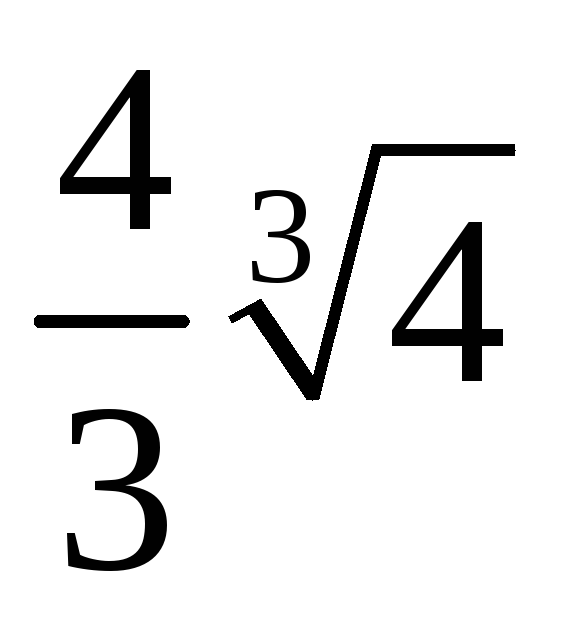
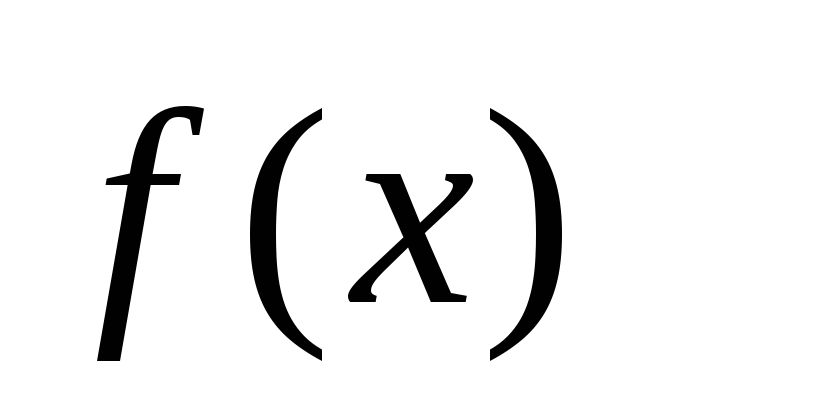
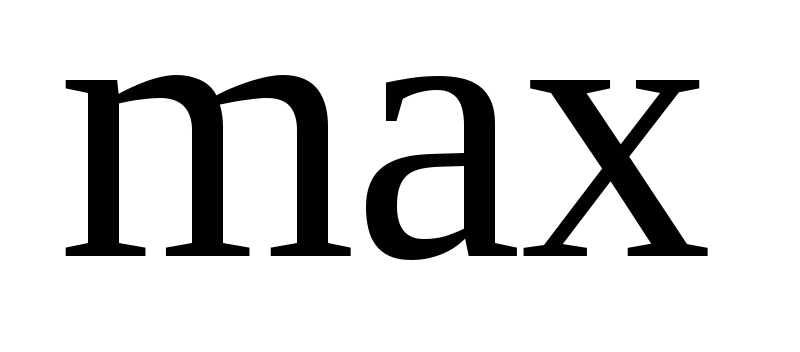
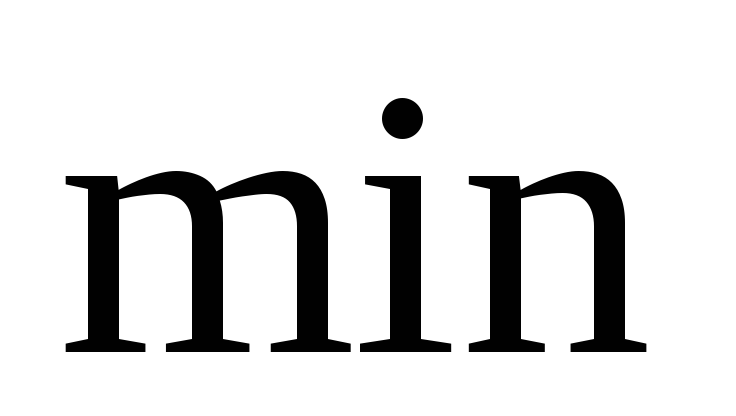
6. Вычислим вторую производную

.

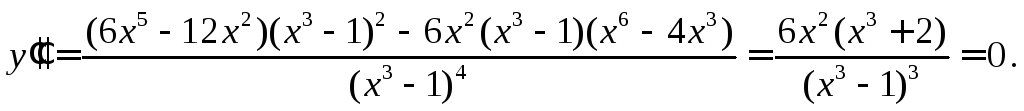
Находим точки, в которых вторая производная обращается в нуль: , и построим таблицу

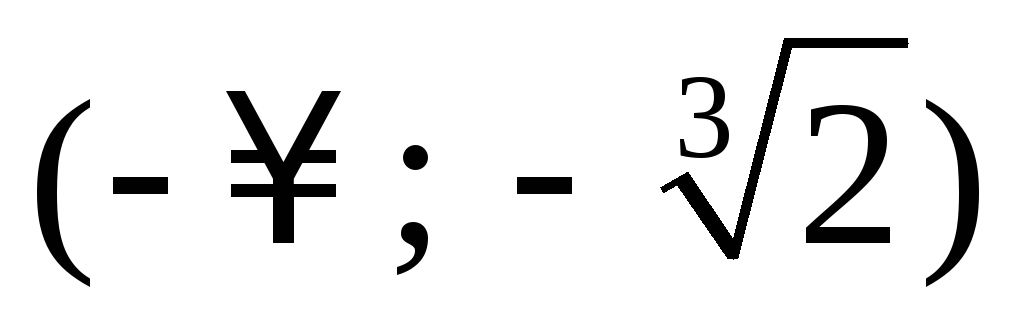
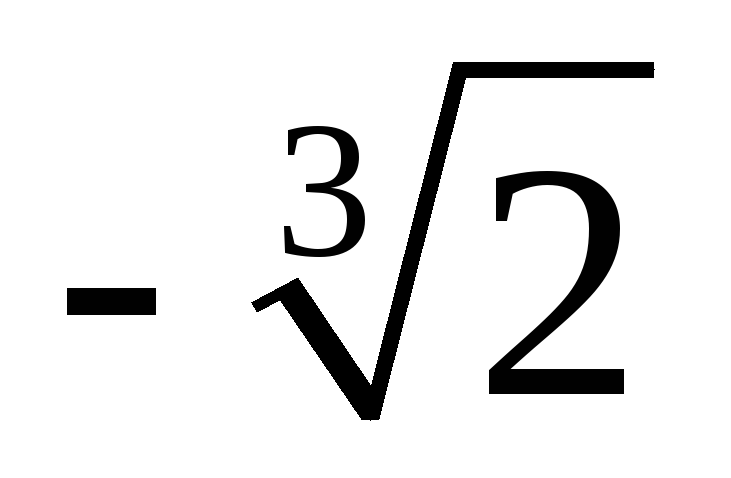
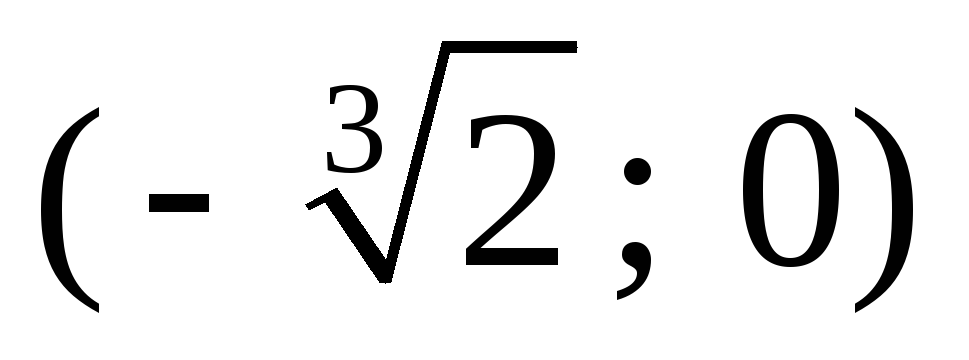
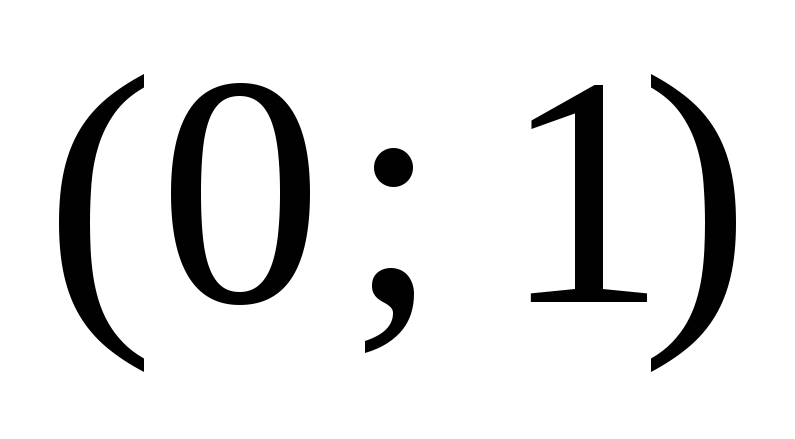
х				0		1
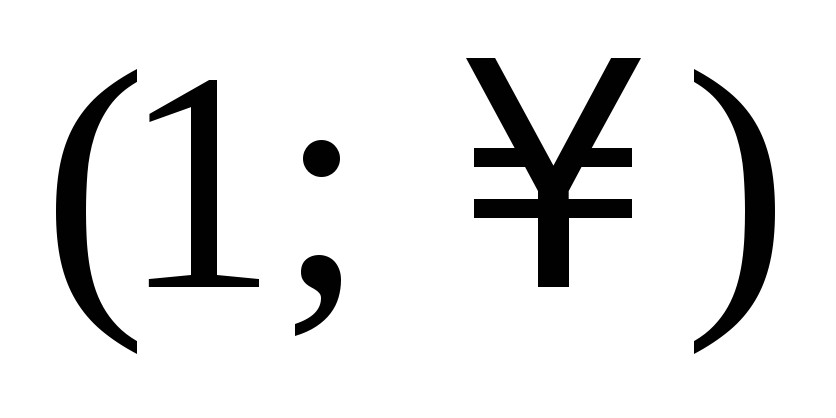
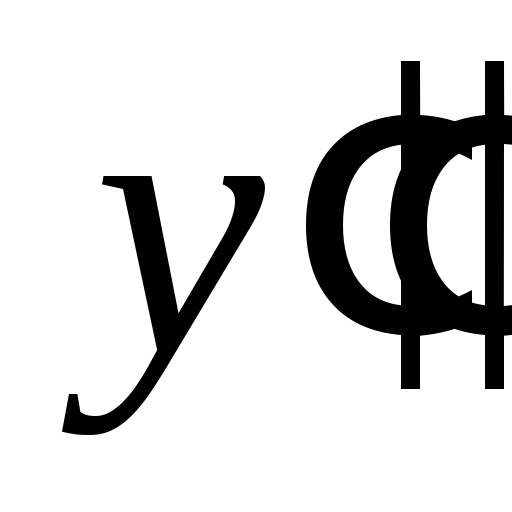
	+	0		0			+
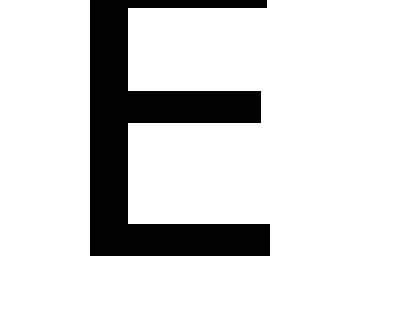
у		перегиб		0

7. Находим асимптоты:

 вертикальная асимптота: ;

 наклонная асимптота:

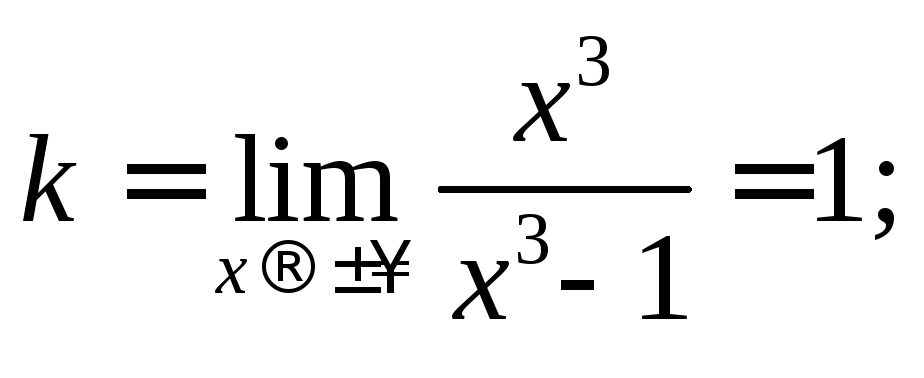
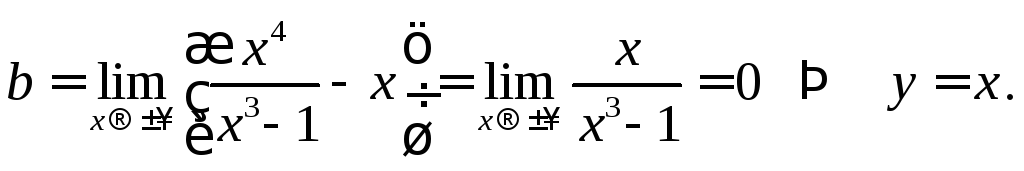
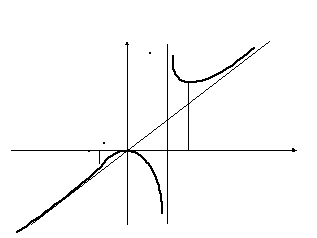8. На основании полученных результатов строим график функции. Это более удобно начинать с построения характерных точек (точки пересечения с координатными осями, точки экстремума, перегиба) и асимптот.

у

О 1 х

6.8*. Кривизна кривой

Напомним, что знак второй производной на некотором интервале определяет выпуклость или вогнутость графика функции на этом интер-вале. В то же время, одни функции более выпуклы (вогнуты), чем другие. Введём понятие, которое характеризует это явление.

Определение 1. Кривизною функции в точкех называется предел

.

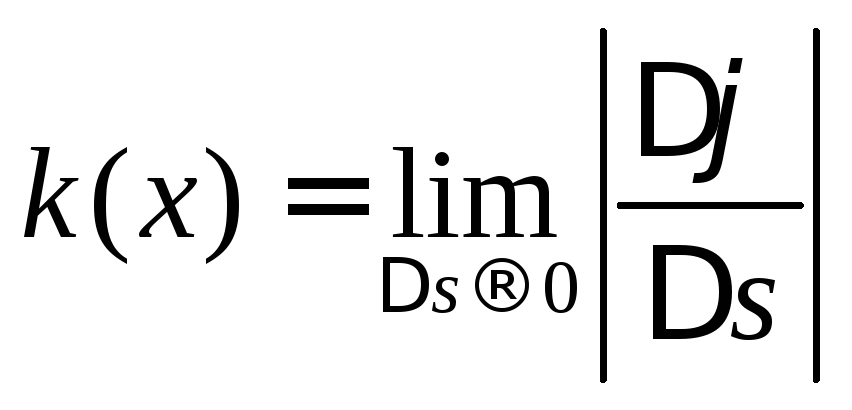y

N

R(x)

М

О x х

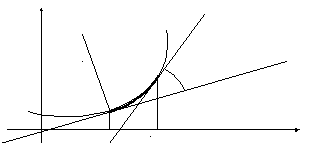
Если воспользоваться таблицей эквивалентных б.м.в., формулой для нахождения угла между двумя прямыми и геометрическим смыслом производной, то для вычисления средней кривизны, получим

.

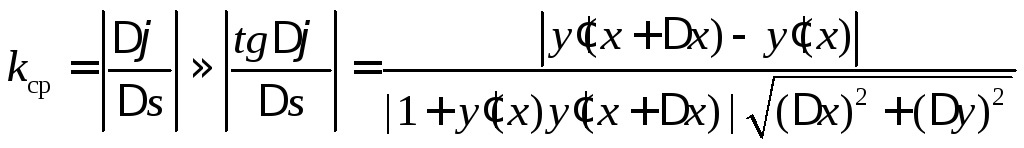Преобразуем это выражение, воспользовавшись теоремой Лагранжа

.

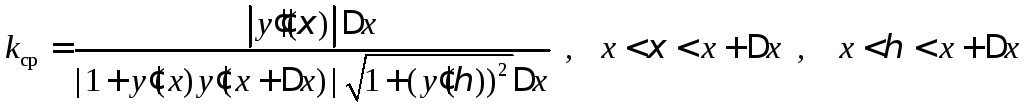Переходя к пределу при и учитывая, что при этом , а и, получаем формулу для вычисления кривизны

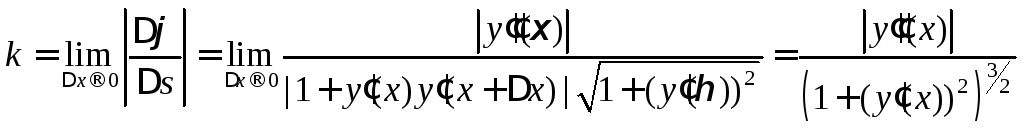. (1)

Для случая, когда линия задана параметрическими уравнениями 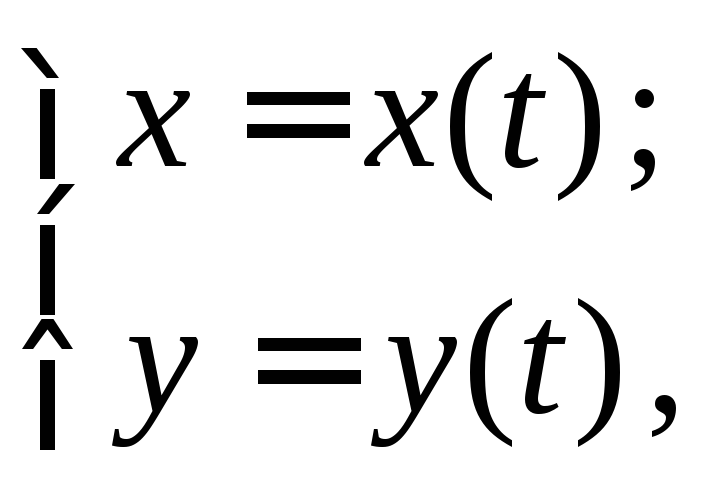с учетом того, что производные

,

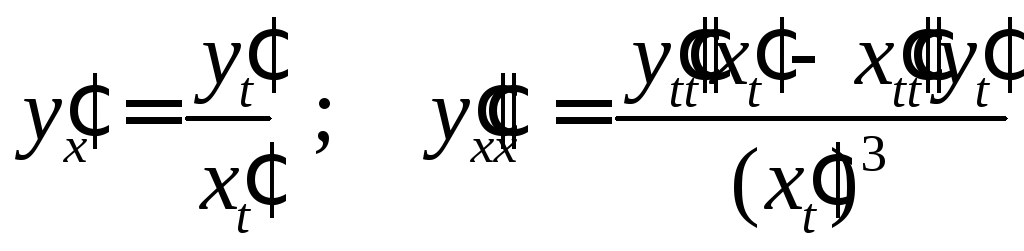из формулы (1) получим

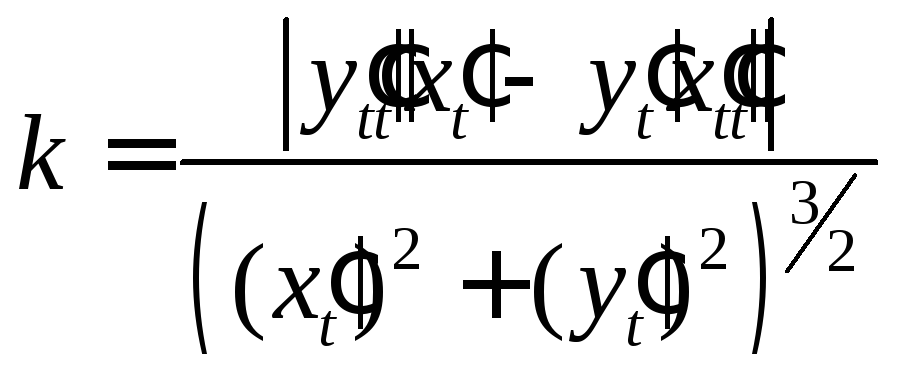. (2)

Определение 2. Величина, обратная кривизне, называется радиусом кривизны: .

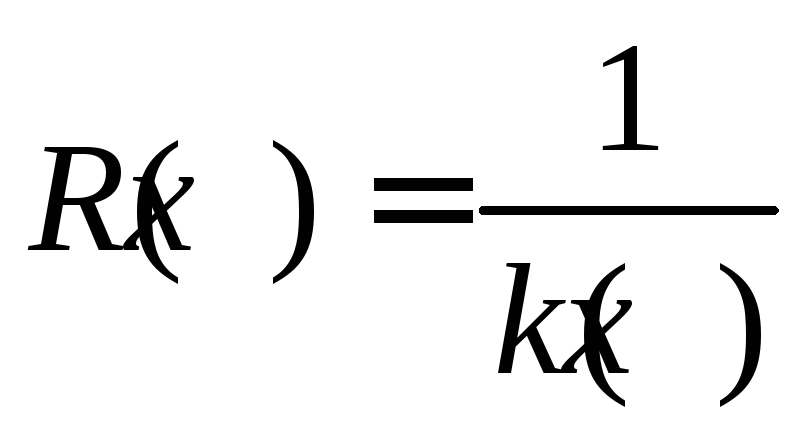Определение 3. Если в сторону вогнутости кривой по направлению нормали отложить отрезок MN, равный радиусу R(x) кривизны линии, то точка N называется центром кривизны в данной точке.

Пример 2. Найти кривизну и радиус кривизны прямой линии .

Так как .

Пример 3. Найти кривизну и радиус кривизны окружности

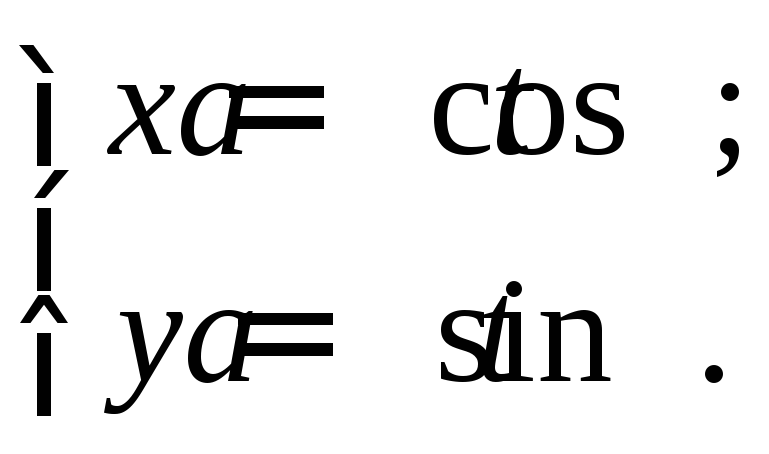
Воспользуемся формулой (2)

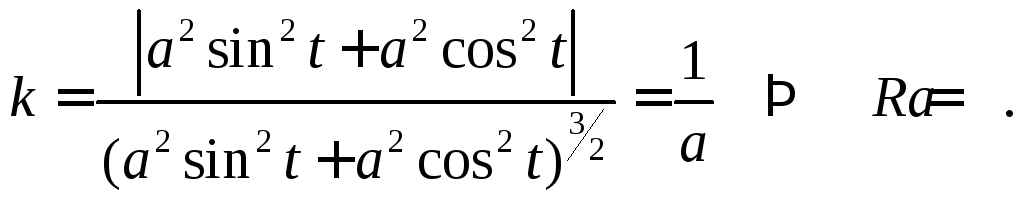
Пример 4. Найти кривизну и радиус кривизны параболы .

Воспользуемся формулой (1)

.

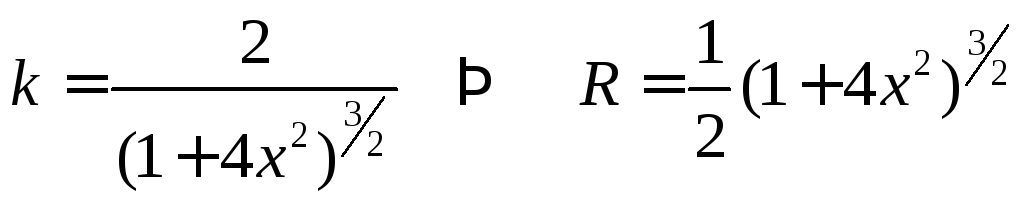Отметим, что наибольшее значение кривизна принимает в вершине параболы.

Определение 4. Множество точек – центров кривизны для данной линии называется эволютой этой линии, а сама линия для своей эволюты – эвольвентой.

Н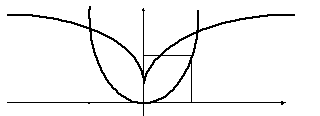апример, для параболы, рассмотренной в предыдущем примере, эволюта имеет следующий вид:

у

эволюта

1 (эвольвента)

О 1х