4.5. Правила дифференцирования

Пусть функции U и V дифференцируемые.

1. Если .

2. .

3. .

4. .

Докажем последнее правило

.

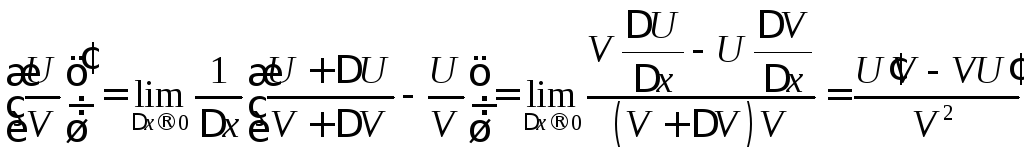Пример 5. Найти производные функций и

.

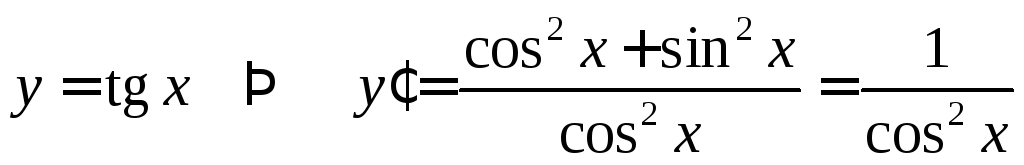Аналогично,

,

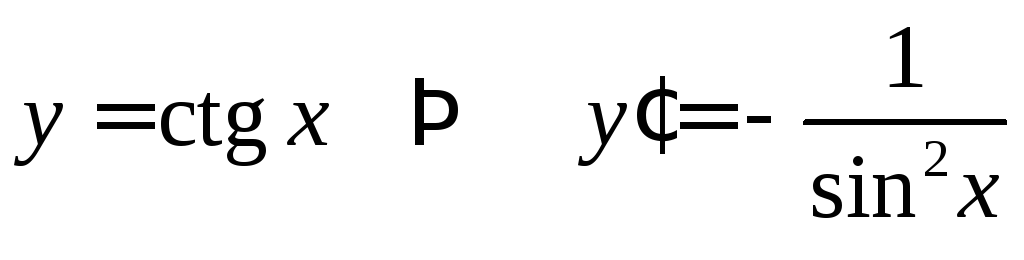т.е. доказаны формулы (8-9) таблицы производных.

4.6. Производная сложной функции

Пусть дана сложная функция , т.е.

Теорема 2. Если функция имеет в точкеx производную , а функцияв соответствующей точкеи также имеет производную , то сложная функцияв точкех имеет производную, которая равна

.

По условию теоремы существует 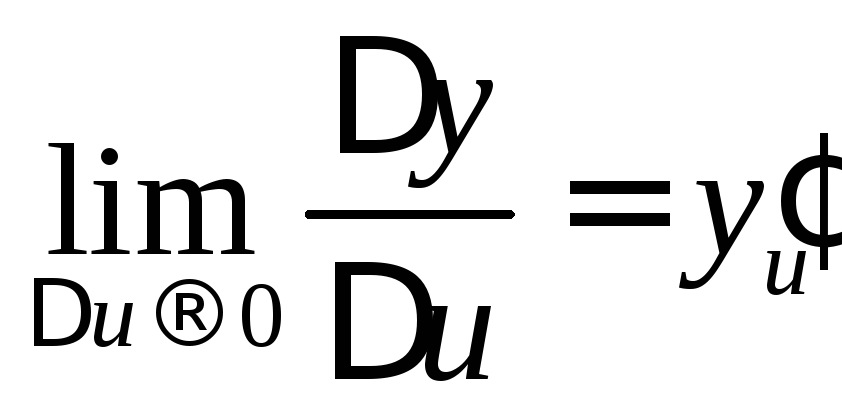. По теореме о пре-деле функции из существования этого предела следует

,

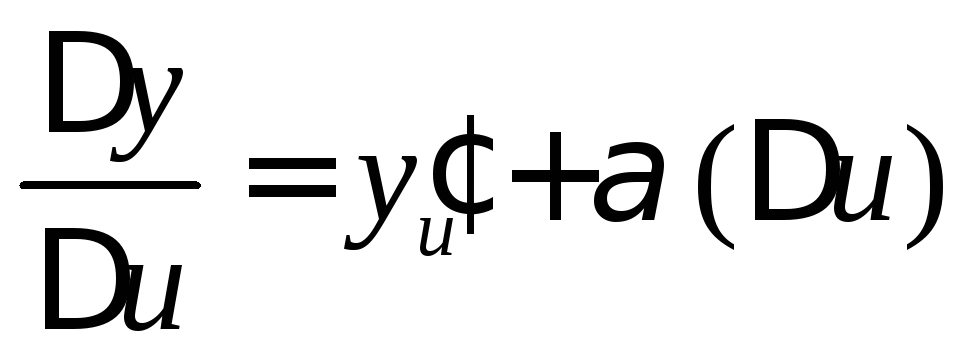где или

. (3)

Разделим выражение (3) на

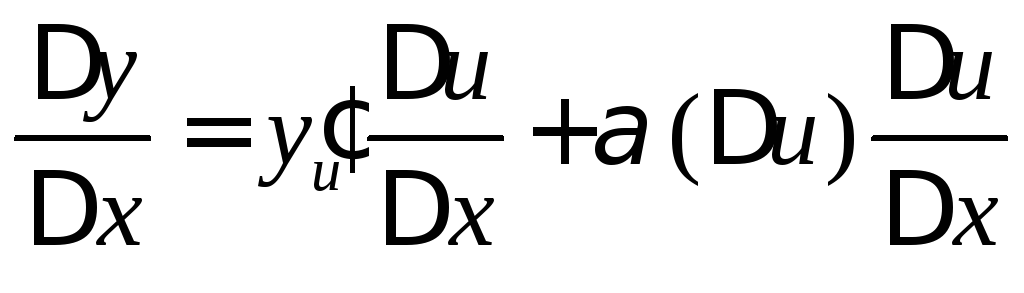. (4)

Переходя к пределу в формуле (4) при , а тогда в силу непрерывности и , получим

. (5)

Замечание 3. Формулу (5) можно обобщить для любого числа суперпозиций функций. Например, если

.

Пример 7. Найти , если.

.

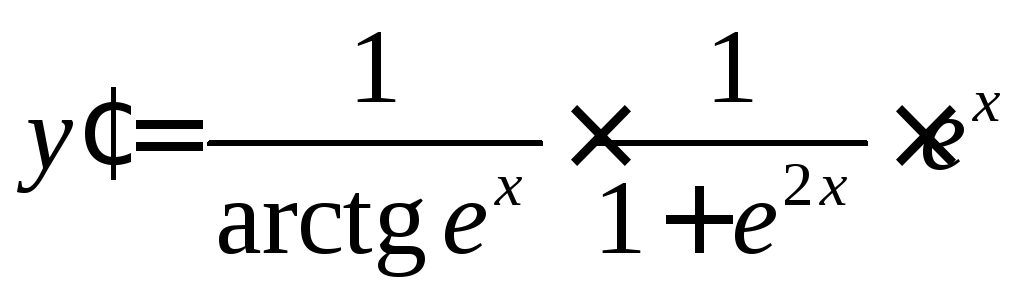Пример 8. Найти , если

Представим и по правилу дифференцирования сложной функции получим

,

т.е. доказана и первая формула из таблицы производных.

Лекция № 19.

4.7. Производная обратной функции

Теорема. Пусть функция монотонна в некоторой окрестности точких и , тогда обратная функциятакже имеет производную в соответствующей точкех, которая определяется по формуле

. (1)

Действительно, в силу монотонности функции для приращенияи тогда

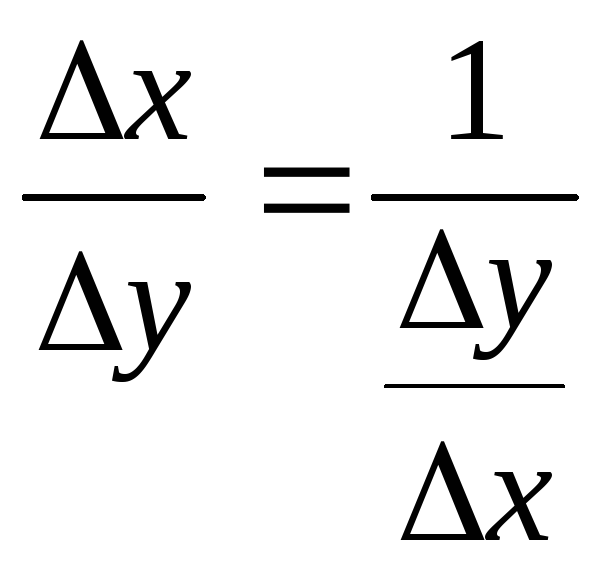. (2)

Если , то в силу непрерывности, и, переходя к пределу в выражении (2), получаем формулу (1).

Пример 1. Найти , если.

Обратная к этой функции есть функция и тогда по формуле (1) получаем

.

Для функции имеем

.

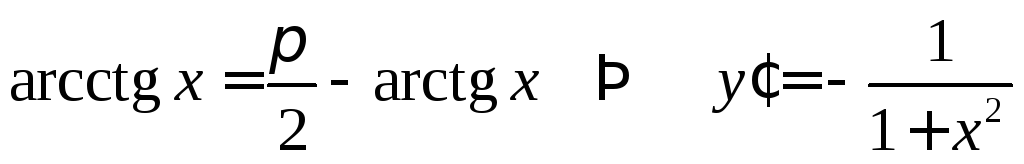Аналогично можно доказать формулы (10-11) таблицы производных.

4.8. Производная функции, заданной параметрическими уравнениями

Пусть функция задана параметрическими уравнениями

тогда справедлива следующая

Теорема. Если функции являются дифференцируемы-ми в соответствующей точке, то

.

Пусть функция имеет обратную функцию, тогда функцияявляется сложной функцией и по правилу дифференцирования сложной функции (4.6) получаем. Если воспользоваться формулой (1), то имеем

.

Пример 2. Составить уравнение касательной к линии при, т.е. в точке.

Имеем

,

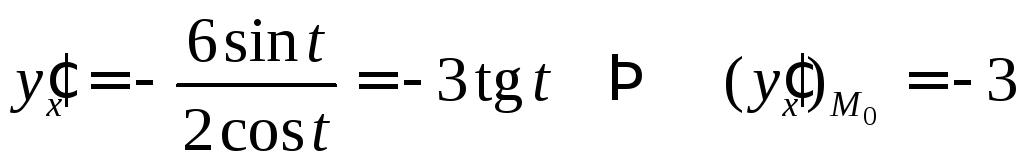тогда уравнение касательной

.

4.9. Производная функции, заданной неявно

Пусть функция задана неявно

(3)

Продифференцируем выражение (3) по аргументу х с учётом, что и разрешим полученное соотношение относительно. Покажем эту процедуру на конкретном примере.

Пример 3. Найти , если.

.

4.10. Производная степенно-показательной функции

Определение 1. Функция вида называется степенно-показательной.

Прологарифмируем эту функцию

. (4)

Дифференцируя обе части выражения (4), получим

или

(5)

Рассмотренная операция называется логарифмическим дифференциро-ванием. Формулу (5) можно удобно запомнить как сумму производных от показательной и степенной функций.

Пример 4. Найти , если.

Прологарифмируем .

Дифференцируя полученное равенство, окончательно имеем

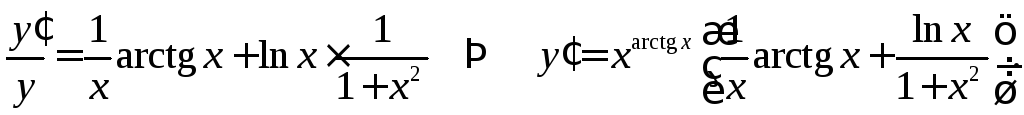
4.11. Производные высших порядков

Если функция дифференцируема, то функцияназывается производной первого порядка и может также быть дифференцируемой функцией, тогда производная от этой функции называется второй производной от функциии обозначается

или .

Вообще производной порядка п от функции называется первая производная от производной (п  1)-го порядка и обозначается

или .

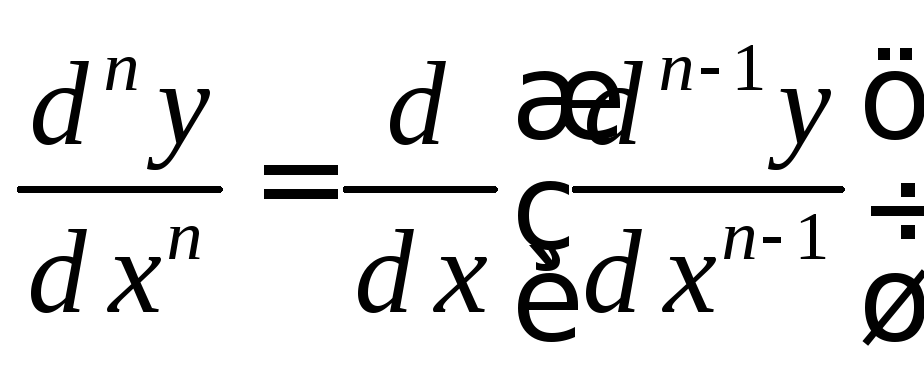Пример 5. Найти п-ю производную от функции .

.

Пусть функция задана параметрическими уравнениями

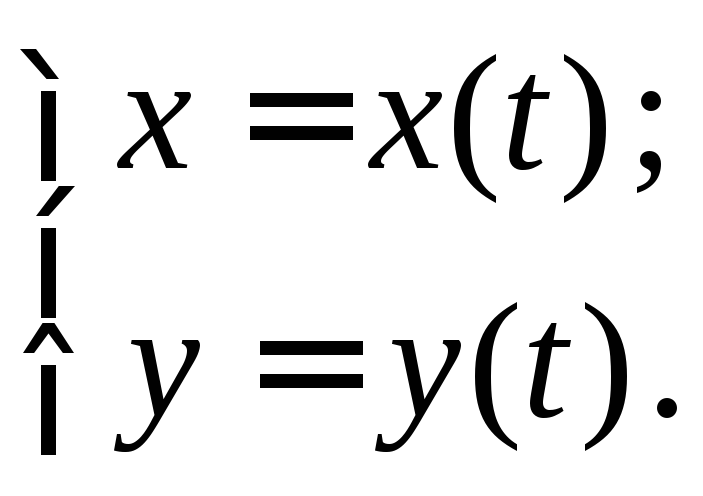
Тогда, как известно,

.

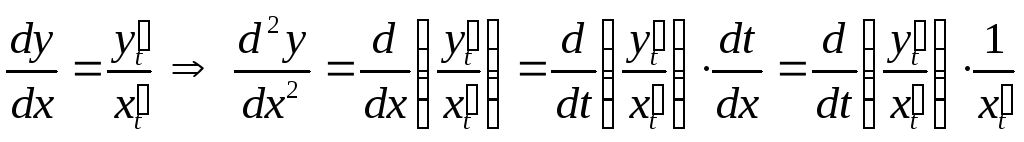Таким образом, в этом случае можно для нахождения использовать следующие формулы:

. (6)

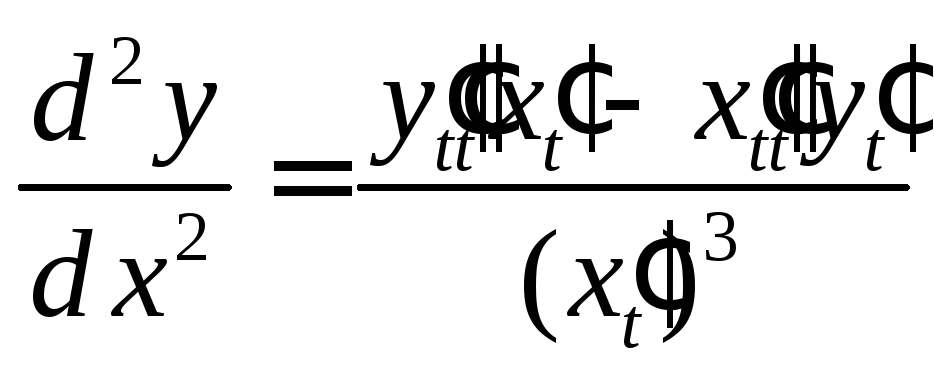. (7)

Формулу (6) удобно использовать, если перед этим уже найдена .

Пример 6. Найти циклоиды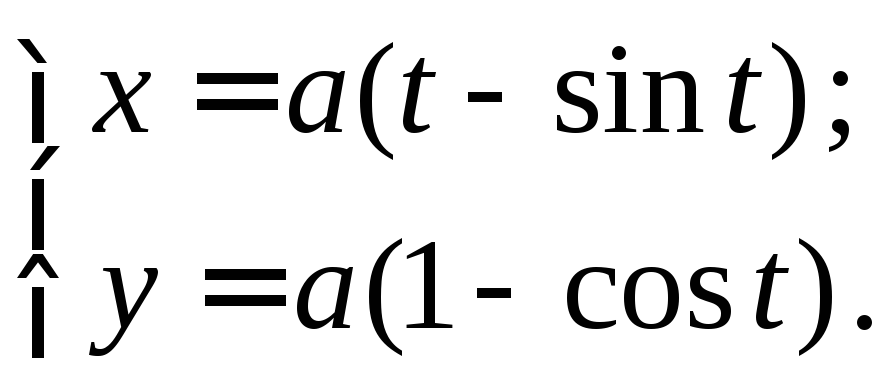

По формуле (7) получаем

.

Нахождение второй производной функции, заданной неявно, рассмот-рим на примере

Пример 7. Найти , если.

Продифференцируем это уравнение

.

Продифференцируем найденную первую производную ещё раз

.

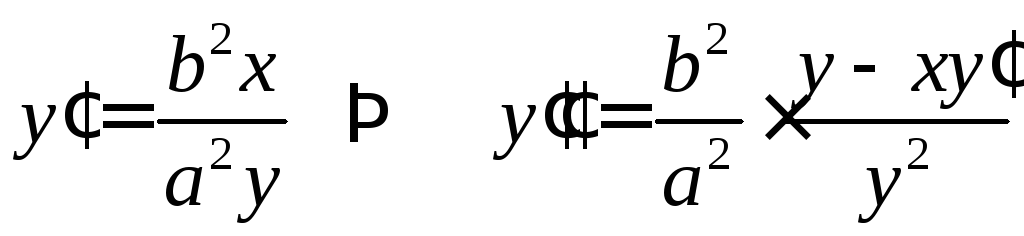С учётом выражения для и самой функции окончательно получим

.

Замечание 1. Аналогично можно находить производные высших поряд-ков от функций, заданных неявно или параметрическими уравнениями.

Замечание 2. Как и для производной первого порядка, можно рас-смотреть механический смысл второй производной, а именно, если  путь, пройденный материальной точкой, то ускорение .