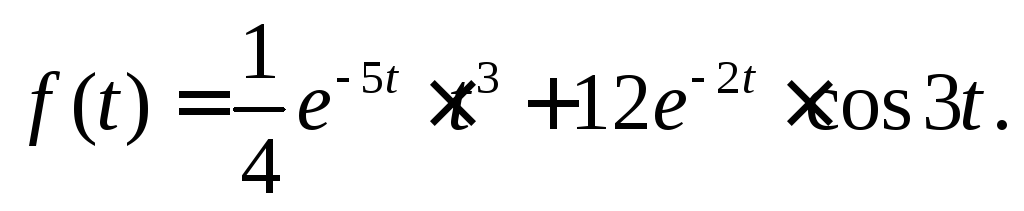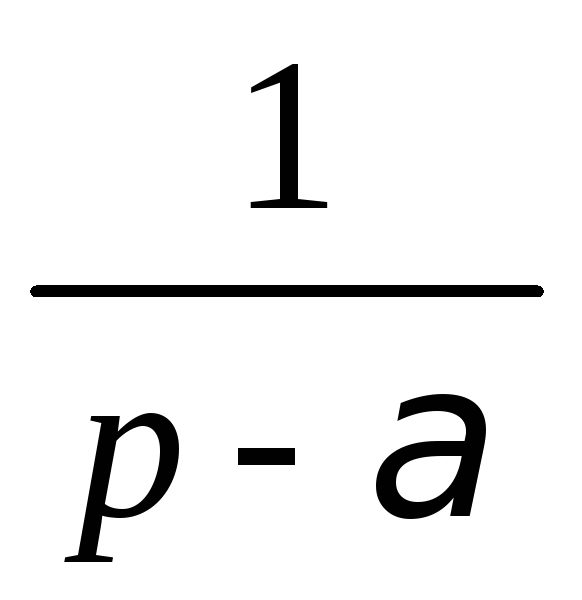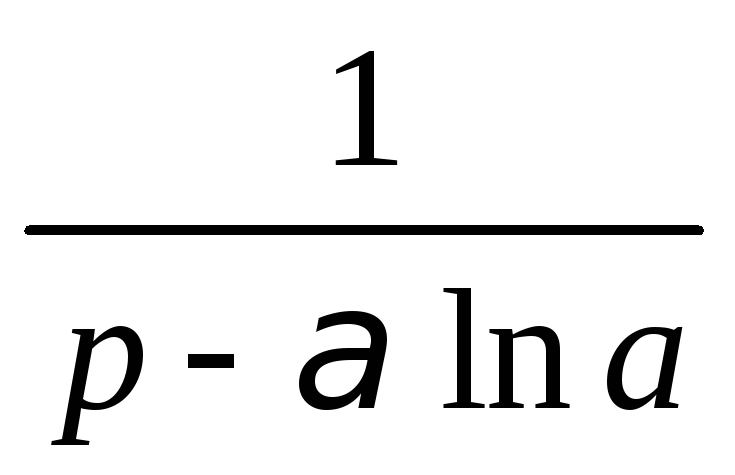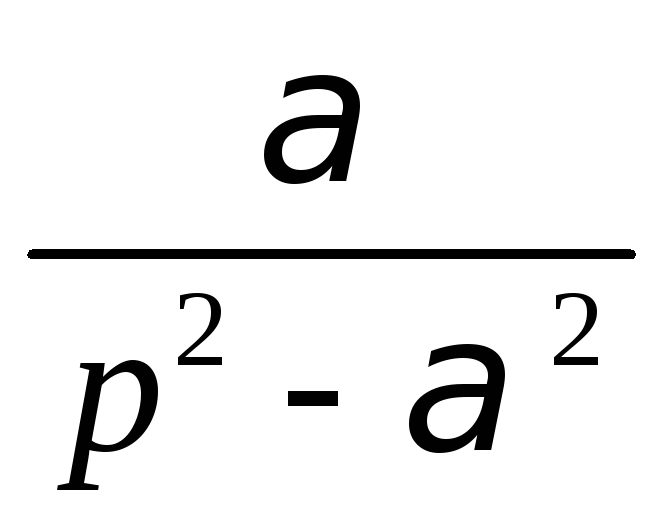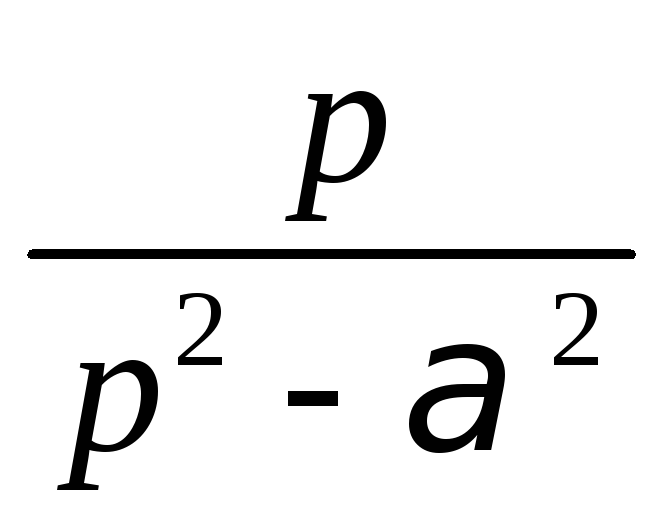Операционное исчисление Лекция № 75. Тема 1 : Оригинал и изображение

1.1. Определение оригинала и изображения

Определение 1. Оригиналом называется функция действительной переменнойt, удовлетворяющая следующим условиям:

1. однозначная и кусочно-непрерывная функция вместе со своими производными;

2.

3. и, что выполняется, гденазывается показателем роста функции.

Определение 2. Изображением оригинала называется функция комплексной переменной , которая определяется интегра-лом Лапласа

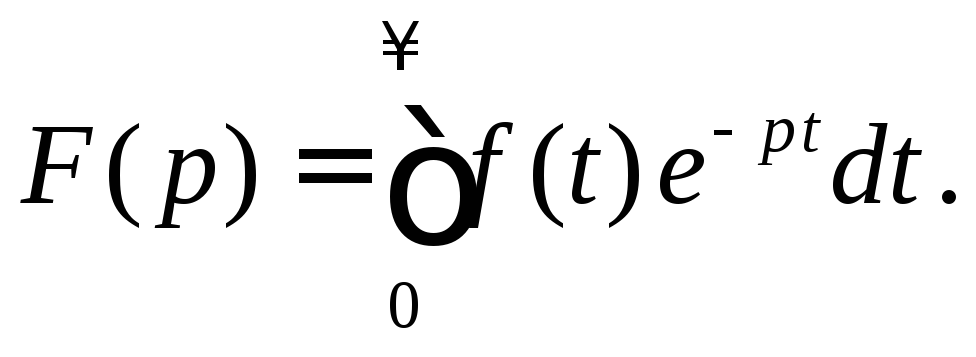(1)

Естественно, что при этом аргумент p должен быть таким, чтобы несобственный интеграл (1) был сходящимся, т.е. . Интеграл (1) называется преобразованием Лапласа функции и обозначается

или

Теорема об обращении преобразования Лапласа. Если оригинал иего изображение, тоимеет место формула обращения (обратное преобразование Лапласа)

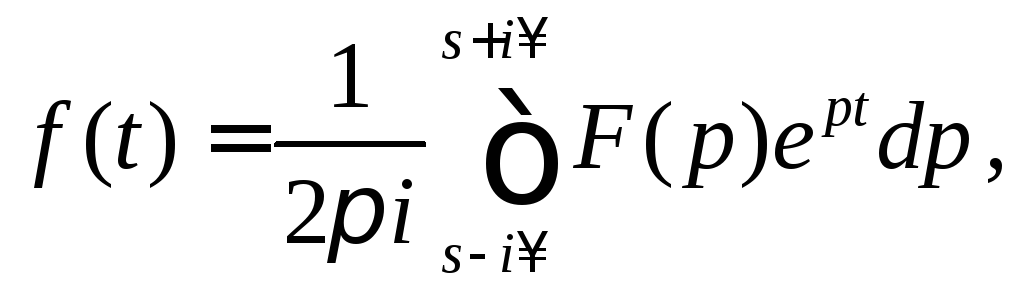(2)

где интегрирование ведется вдоль прямой , параллельной мнимой оси. Формулу (2) символически записывают

.

Основные свойства преобразования Лапласа:

1. Преобразование Лапласа обладает свойством линейности, т.е.

где

2. Всякое изображение приявляется аналитической функцией;

3. Если  изображение функции , то

1.2. Изображения некоторых функций

1. Единичная функция

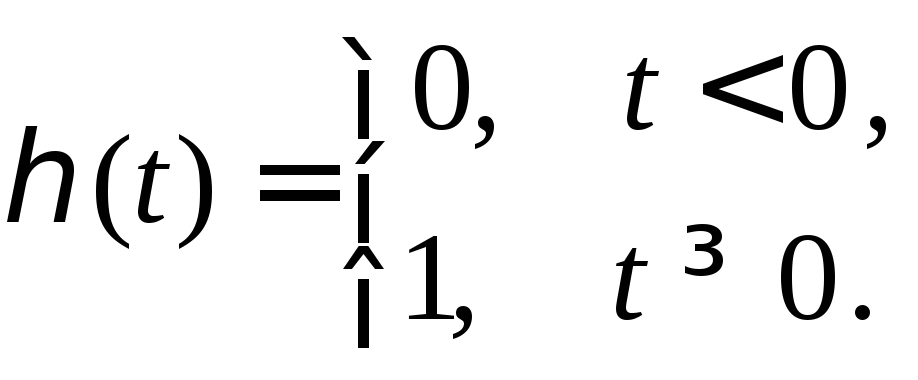
Тогда

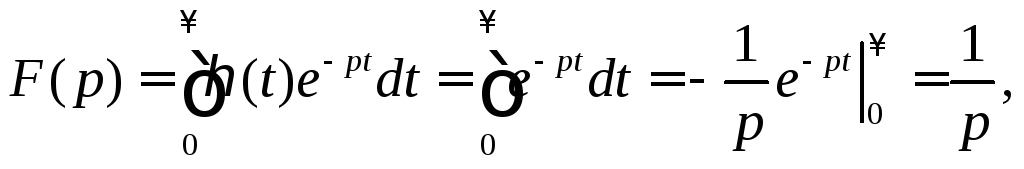
т.е. 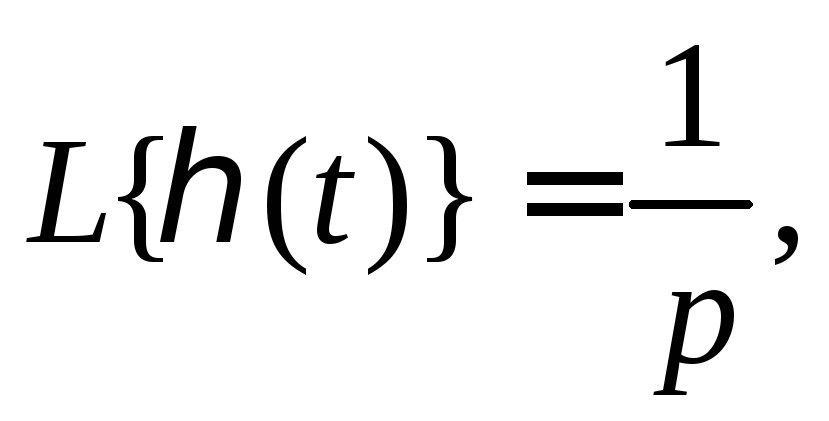если

Замечание. Из определения преобразования Лапласа следует, что в дальнейшем преобразование Лапласа будет осуществляться для функций вида

2. Степенная функция где

Найдем изображение функции т.е. рассмотрим случай, когдаТогда имеем

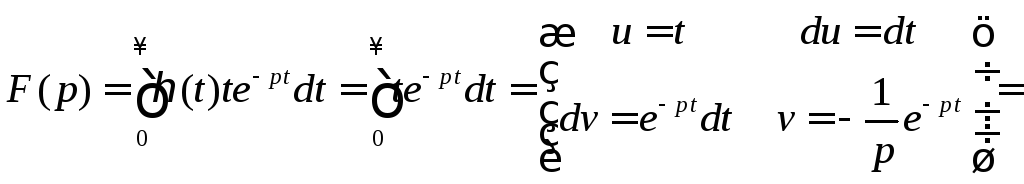
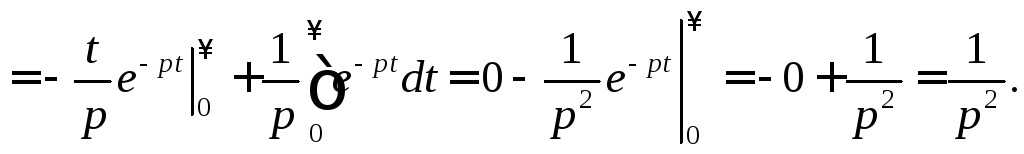
Аналогично, применяя формулу интегрирования по частям n раз, получим окончательную формулу

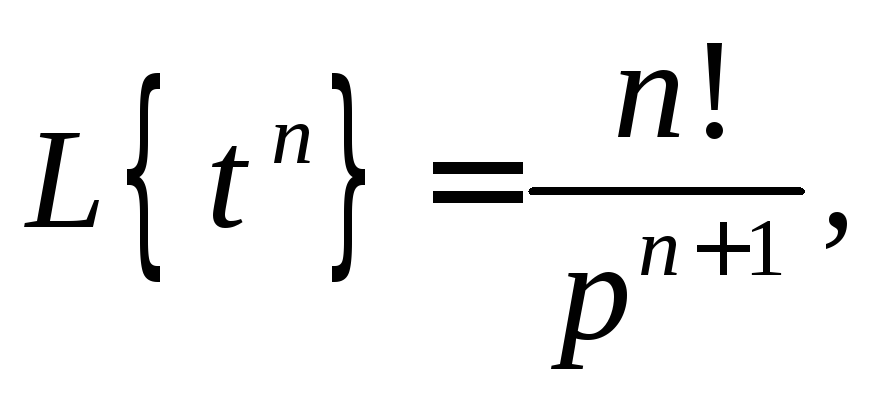если

3. Показательная функция

Аналогично получим 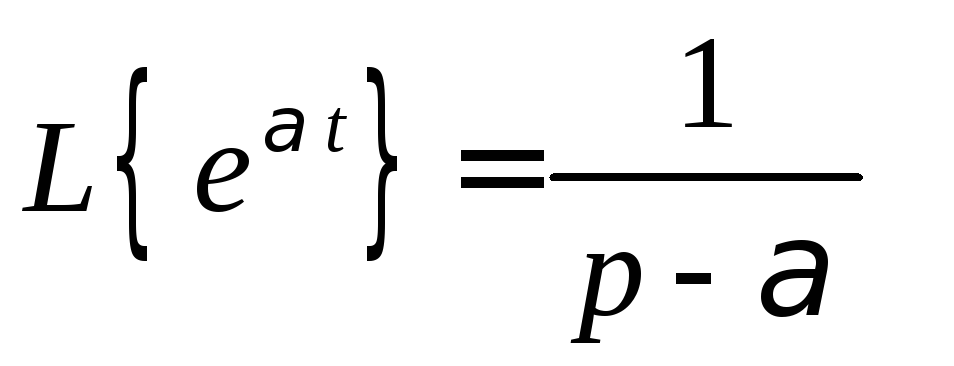, если

4. Гиперболические функции

Так как

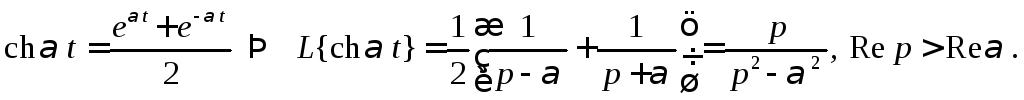
Аналогично получим

5. Тригонометрические функции

Как известно, тригонометрические функции можно выразить через показательные функции, поэтому получим

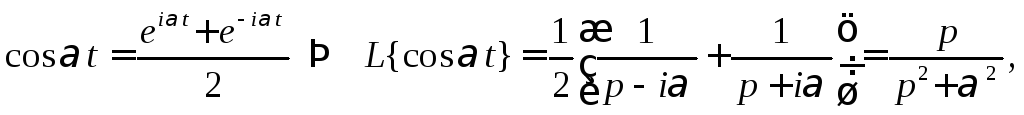
где

Аналогично имеем

где

Все полученные результаты внесем в таблицу.

Оригинал	Изображение		Оригинал	Изображение

Пример 1. Найти изображение функции

Используя свойство линейности преобразования Лапласа и таблицу изображений, получим

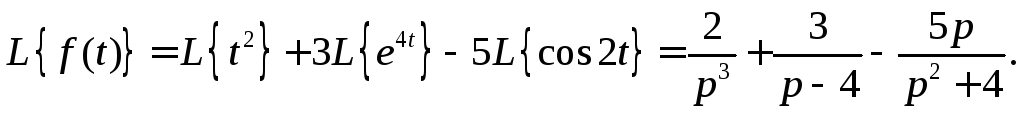
Тема 2 : Основные теоремы операционного исчисления

2.1. Теоремы подобия, запаздывания и смещения

Теорема 1 (подобия).

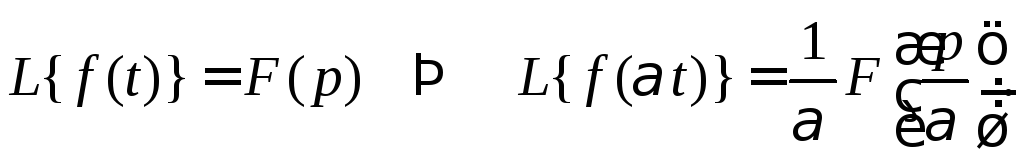
Воспользуемся определением преобразования Лапласа и выполним замену переменной:

Теорема 2 (запаздывания).

Из определения оригинала следует, что при или, поэтому имеем

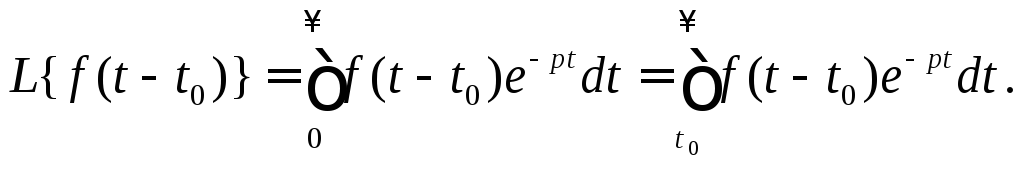
Выполним замену переменной в последнем интеграле:

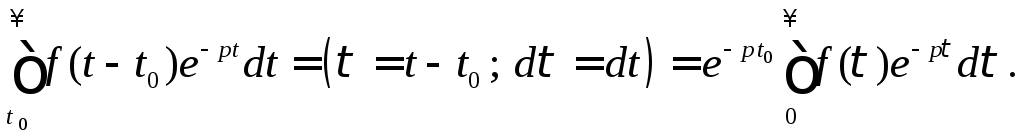
Таким образом, окончательно получим

Пример 2. Найти изображение функции

Используя свойство линейности преобразования Лапласа, таблицу изображений, теоремы подобия и запаздывания, получим

Аналогично доказывается и следующая

Теорема 3 (смещения).

Пример 3. Найти изображение функции

Используя свойство линейности преобразования Лапласа, таблицу изображений, теоремы подобия и смещения, получим

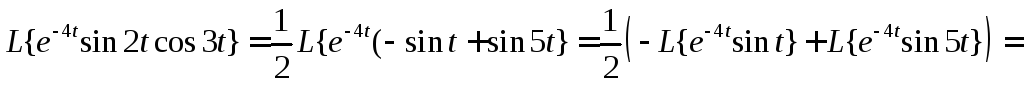
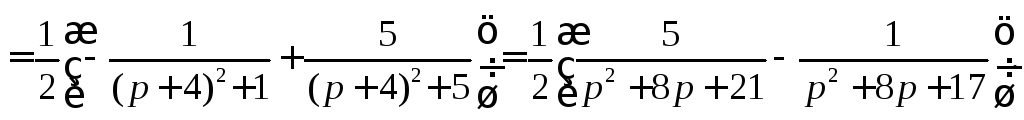
Пример 4. По данному изображению

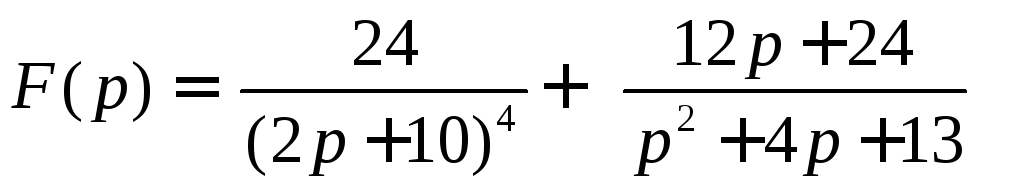
найти оригинал.

Представим данное изображение в виде

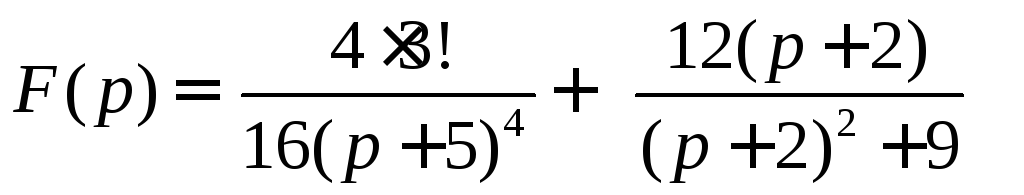
и воспользовавшись таблицей изображений и теоремой смещения, переходя от изображений к оригиналам, получим