Лекция № 76.

2.2. Теорема о свёртке

Определение 1. Выражение вида

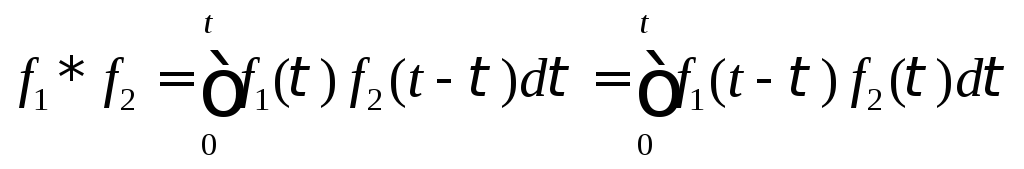
называется свёрткой функций и .

Теорема. Если и , то

.

Действительно,

= (во внутреннем интеграле заменим переменную) = =

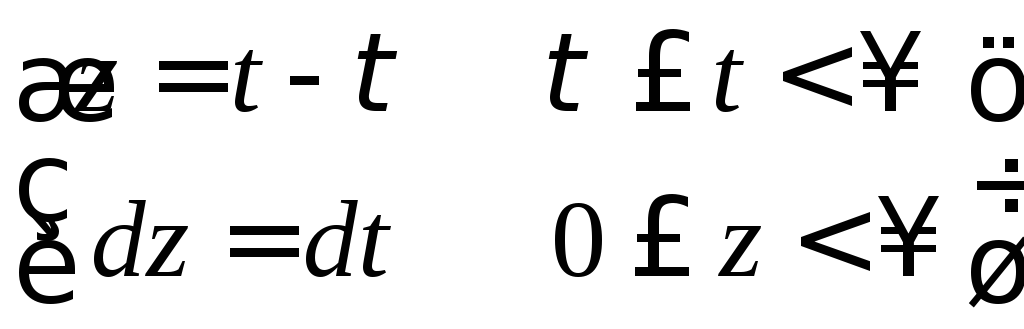Пример 1. По изображению 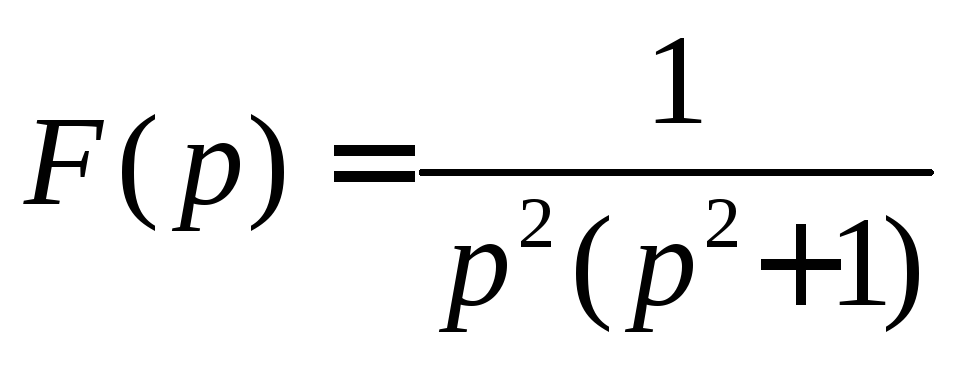найти оригинал.

Из таблицы изображени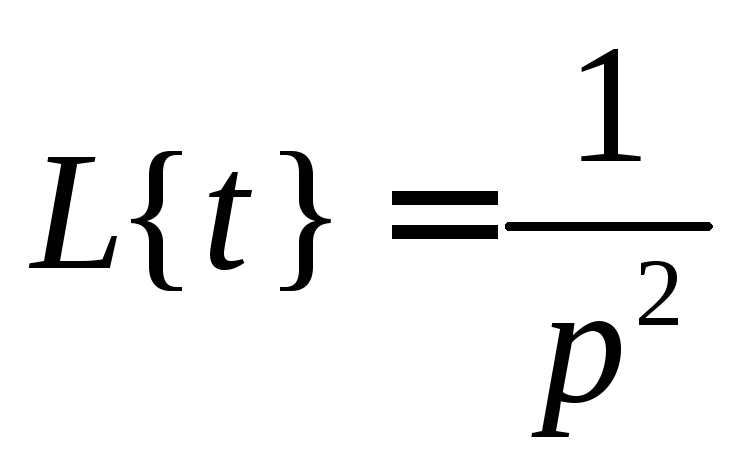й

и

поэтому по теореме о свёртке получим

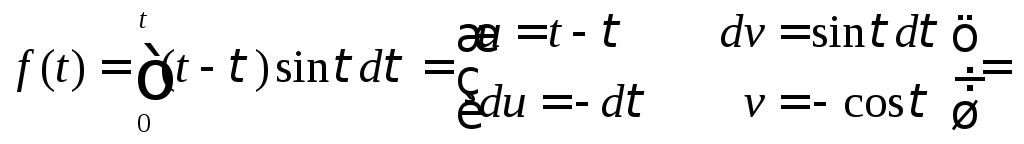
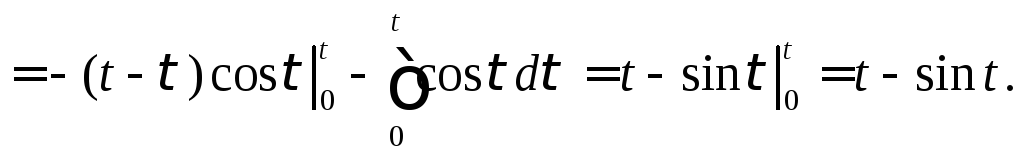
2.3. Теорема о дифференцировании оригинала

Теорема. Если , то

Докажем эту формулу для первой производной, применив формулу интегрирования по частям:

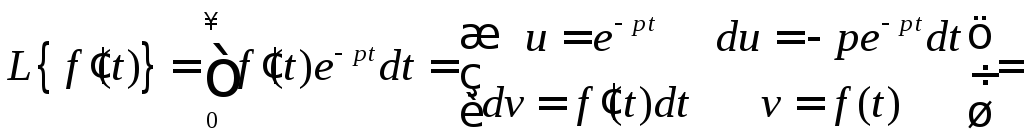
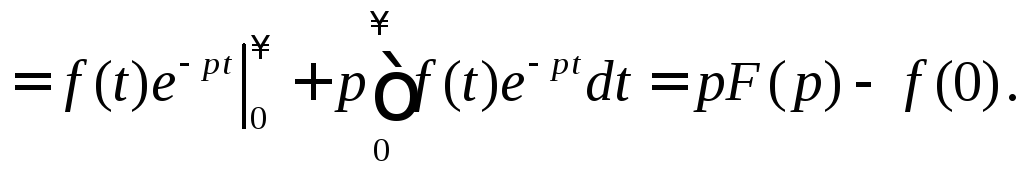
Аналогично, применяя формулу интегрирования по частям п раз, получим изображение п-ой производной.

Пример 2. Найти изображение функции , воспользовавшись теоремой о дифференцировании оригинала.

2.4. Теорема о дифференцировании изображения

Теорема.

Доказывается дифференцированием по р преобразования Лапласа.

Пример 3. Найти изображение функции , воспользовав-шись теоремой о дифференцировании изображения.

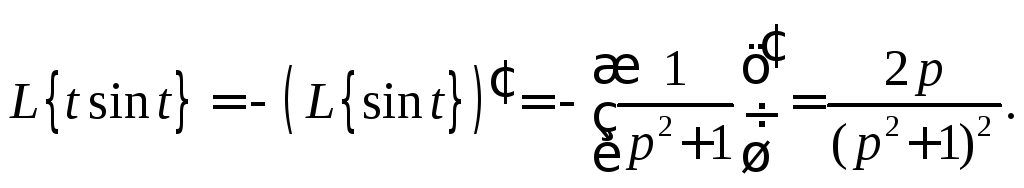
2.5. Теорема об интегрировании оригинала

Теорема. Если , то

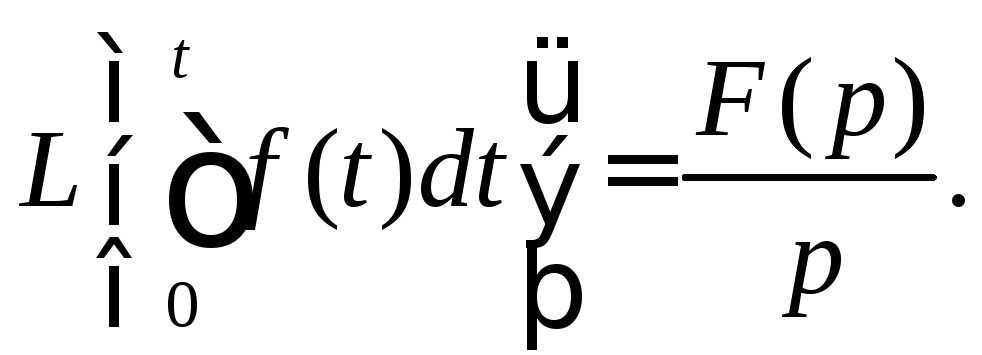
Пусть и

тогда по теореме о дифференцировании оригинала получаем

или

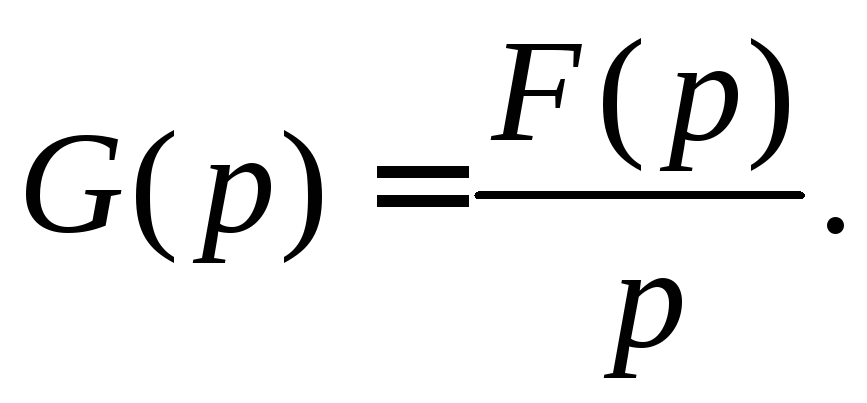
Пример 4. Найти изображение функции

Воспользуемся результатом примера 3 и теоремой об интегрировании оригинала:

2.6. Теорема об интегрировании изображения

Теорема. Пусть , тогда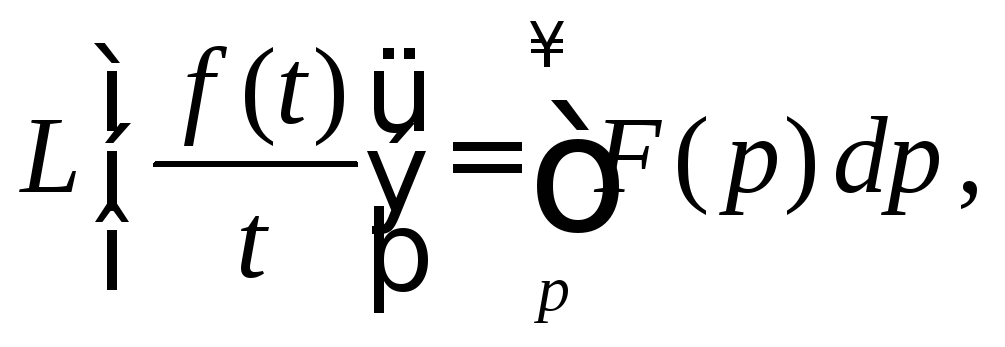если интеграл сходится.

Преобразуем интеграл

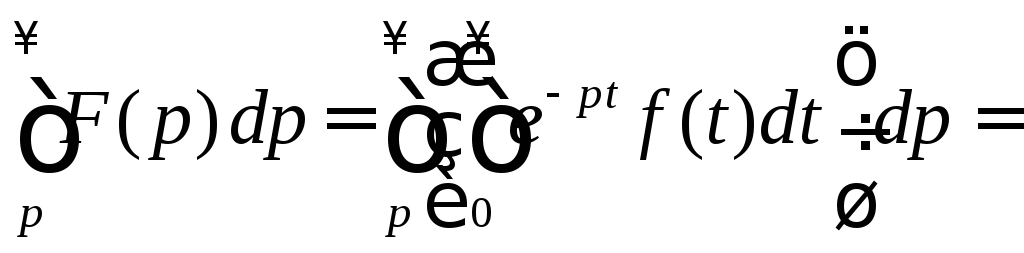
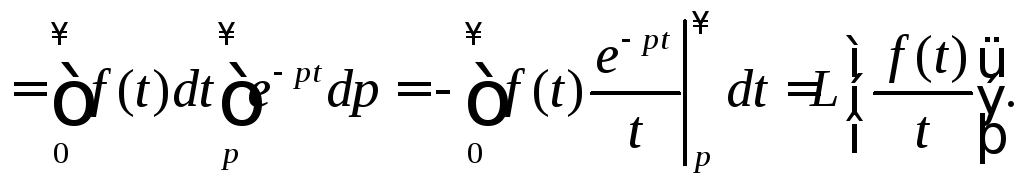
Пример 5. Найти изображение функции

Так как по теореме смещения

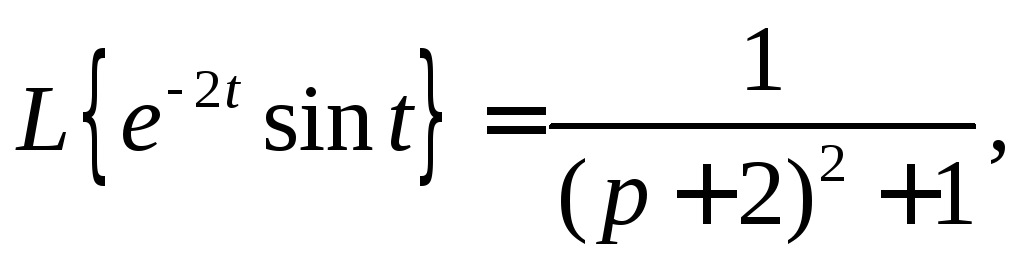
то

2.7. Теорема разложения

Теорема. Если ,

то

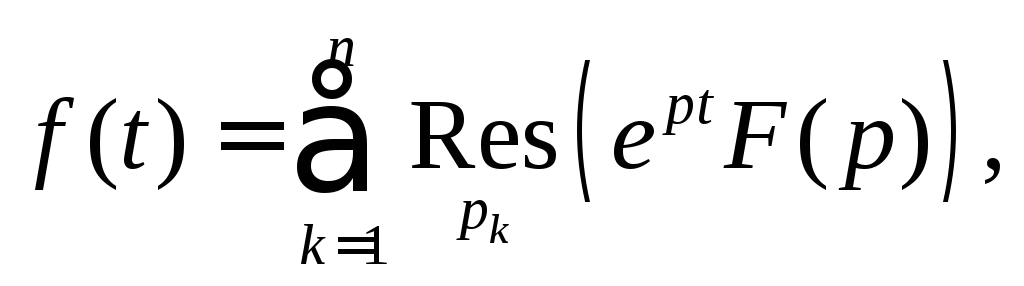
где  особые точки функции . R

O s

Рассмотрим интеграл

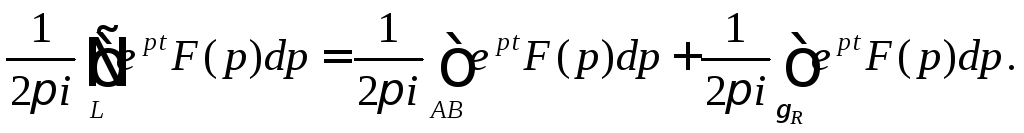(1)

Переходя в выражении (1) к пределу при , и учитывая, что

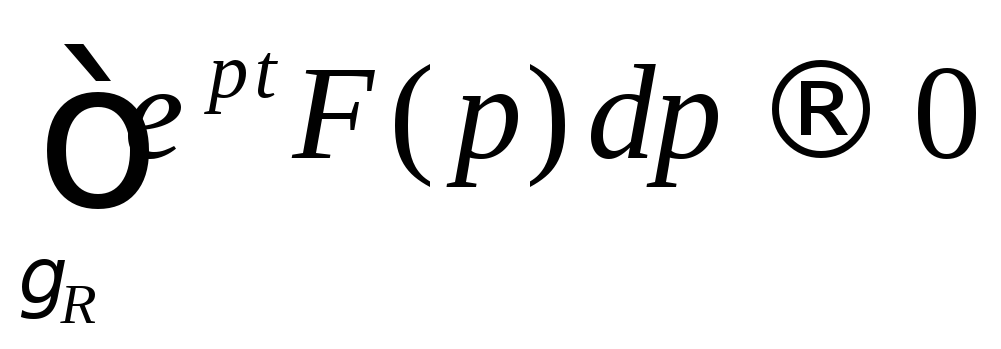(лемма Жордана),

получим

т.е.

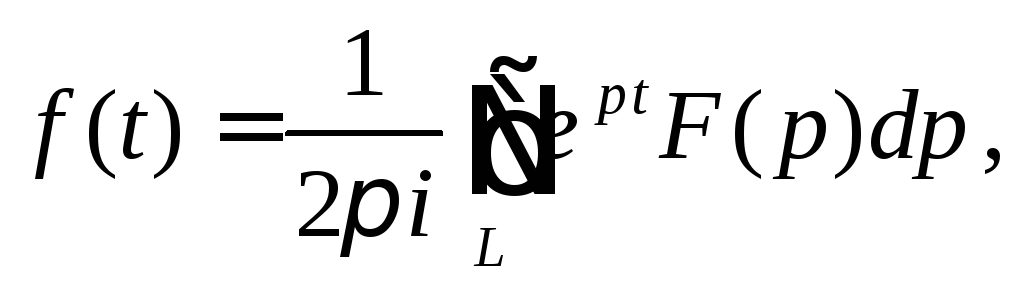
где L  контур, внутри которого находятся все особые точки функции . По теореме о вычетах получаем

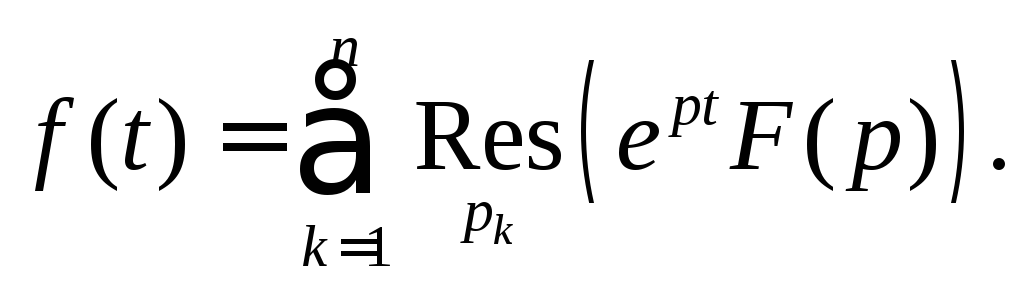
Рассмотрим частные случаи теоремы.

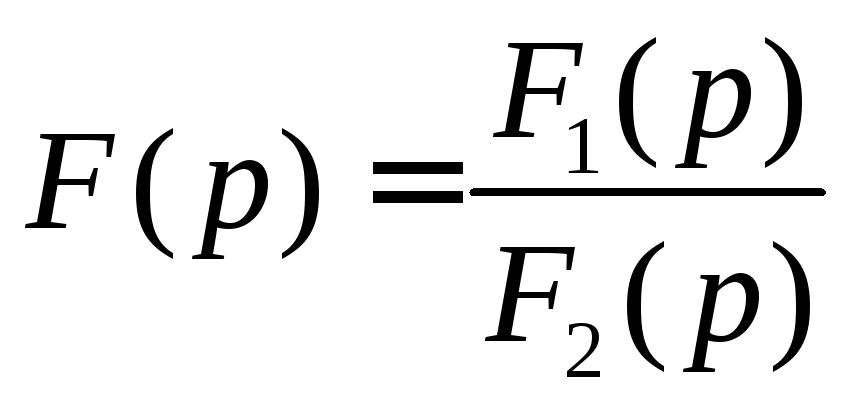
Пусть  правильная рациональная дробь.

Тогда функция имеет конечное число полюсов. Здесь возмож-ны два случая:

1. Случай простых полюсов.

Тогда по теореме о вычетах получаем

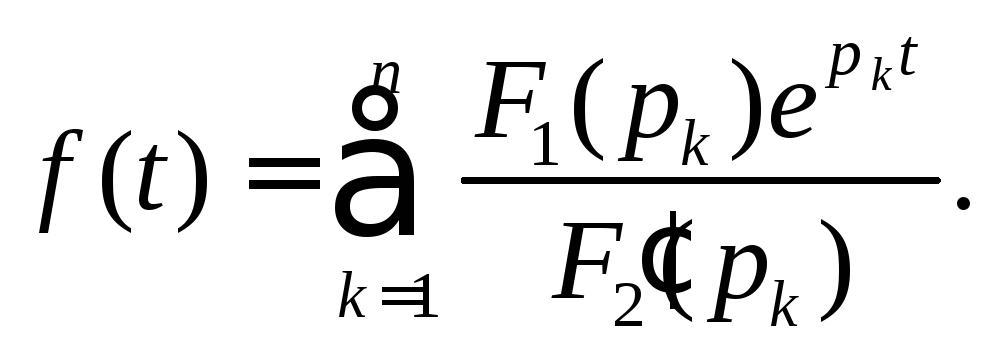(2)

2. Случай кратных полюсов ( кратность k-го полюса).

Аналогично

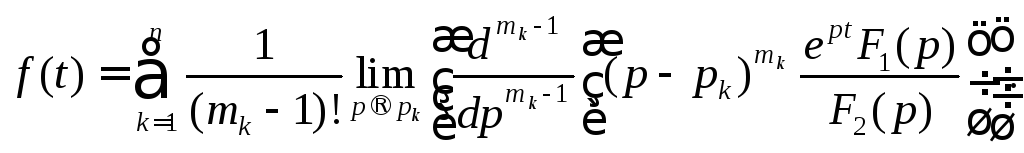(3)

Замечание. Если изображение имеет комплексно-сопряженные полюсы , то можно показать, что и вычеты в этих точках будут комплексно-сопряженными, и тогда

.

Пример 6. По изображению 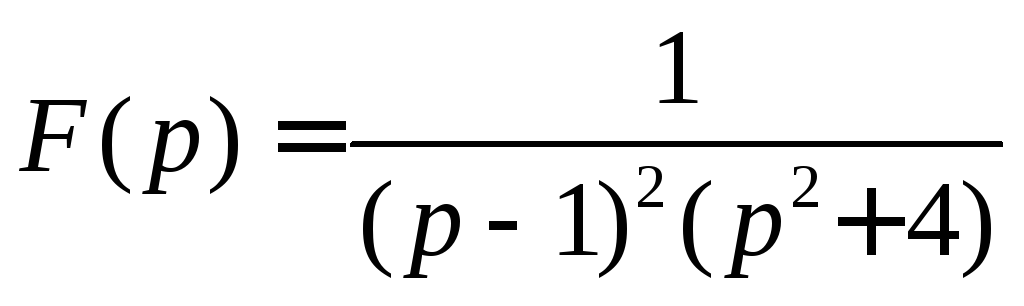найти оригинал.

Здесь Тогда функция имеет двукратный полюс и простой комплексно-сопряженный . Применяя формулы (2) и (3), получим

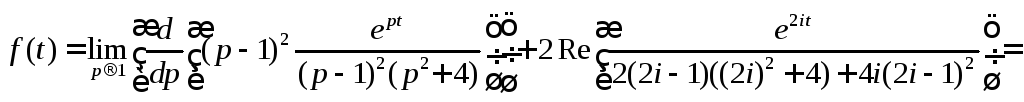
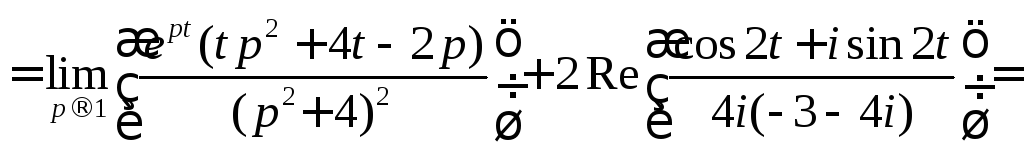
Лекция № 77. Тема 3 : Приложения операционного исчисления

3.1. Решение линейных дифференциальных уравнений и

систем с постоянными коэффициентами

Пусть требуется найти решение дифференциального уравнения

(1)

при начальных условиях: .

Здесь  искомая функция, а

Обозначим .

Тогда, применяя к обеим частям уравнения (1) преобразование Лапласа и используя теорему о дифференцировании оригинала, после перегруп-пировки слагаемых получим

.

Отсюда находим изображение искомой функции

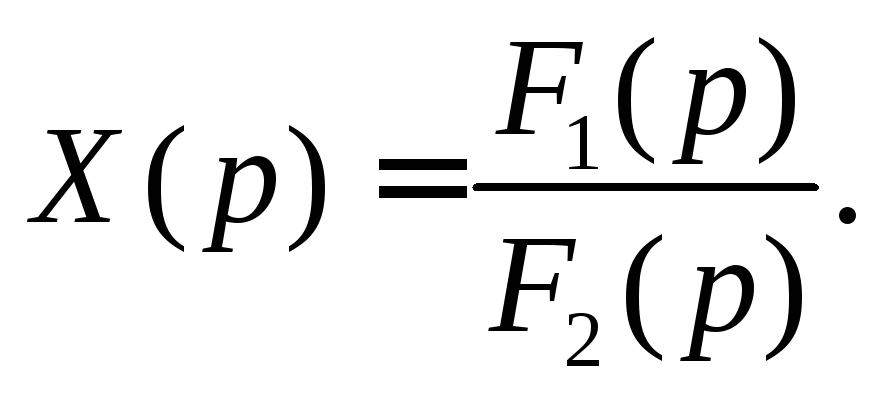(2)

Затем по изображению (2) определяем оригинал .

Проиллюстрируем этот метод на конкретном примере.

Пример 1. Найти решение уравнения при начальных условиях: .

Применим преобразование Лапласа к обеим частям уравнения:

.

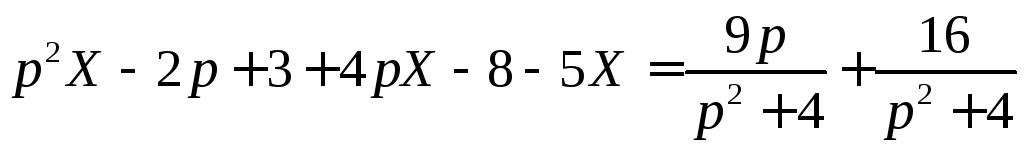Отсюда определяем изображение искомой функции

.

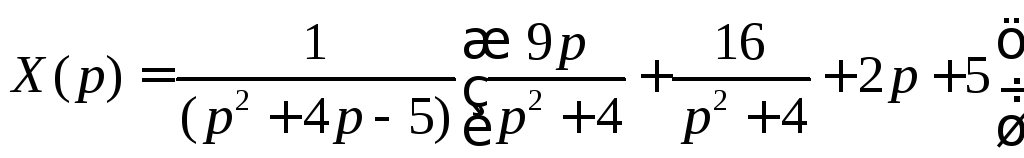После преобразований находим

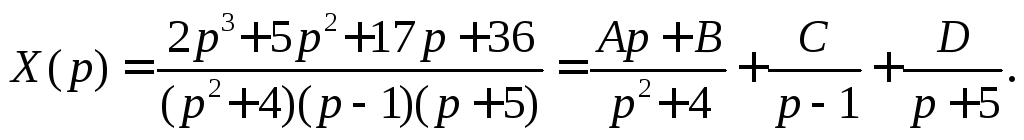
Применим метод неопределённых коэффициентов

.

Из данной системы определяем . Тогда

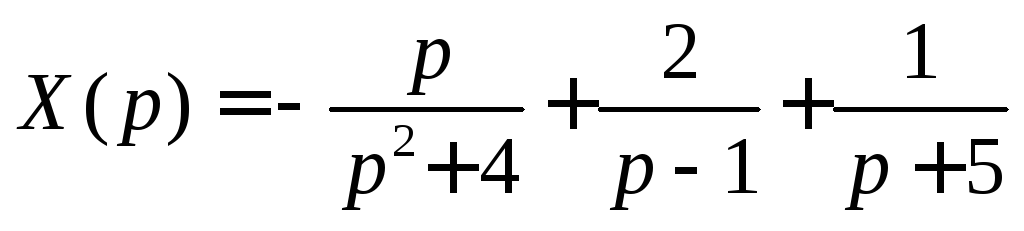
и по таблице изображений находим искомую функцию

Решение систем рассмотрим для случая двух уравнений.

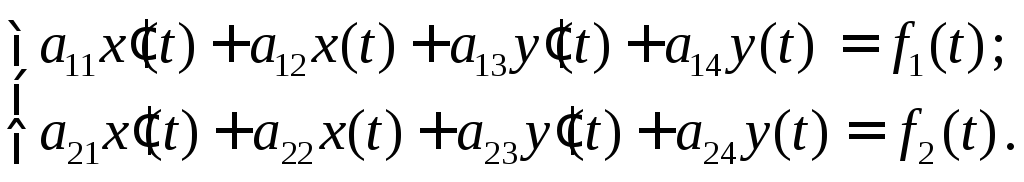
с начальными условиями:

Обозначим

Тогда, применяя к обеим частям уравнений системы преобразование Лапласа и используя теорему о дифференцировании оригинала, получим систему для определения изображений искомых функций

.

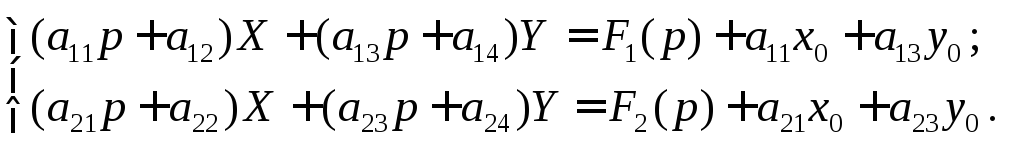Из полученной системы находим изображения и , по которым определяем решение системы дифференциальных уравнений: и .

Пример 2. Найти решение системы уравнений

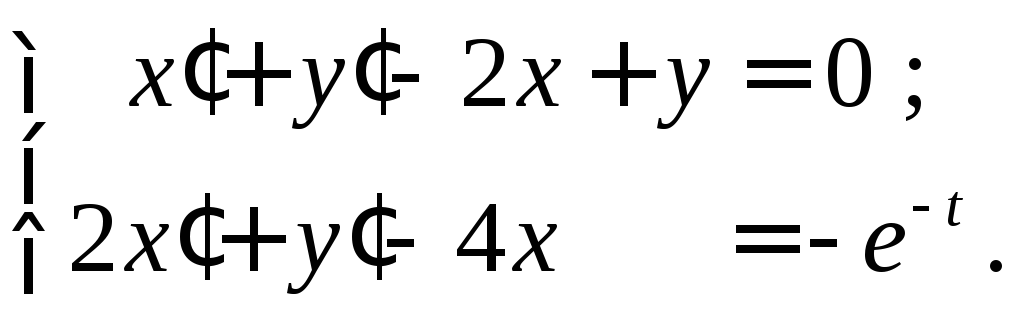
при начальных условиях

Применяя преобразование Лапласа, получаем систему линейных алгебраических уравнений

из которой определяем

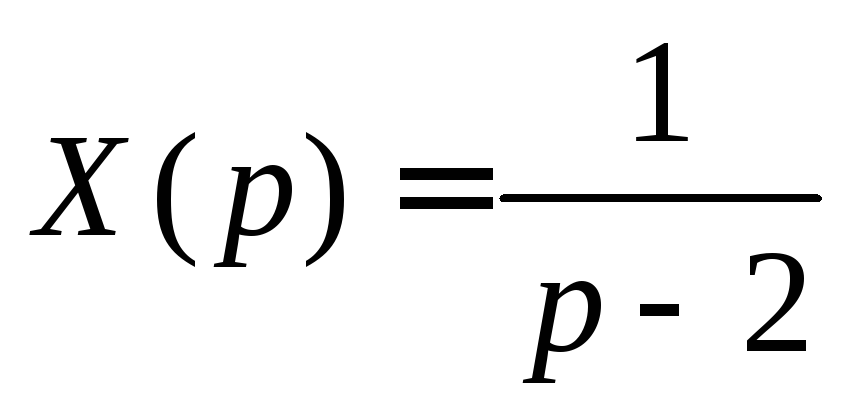и

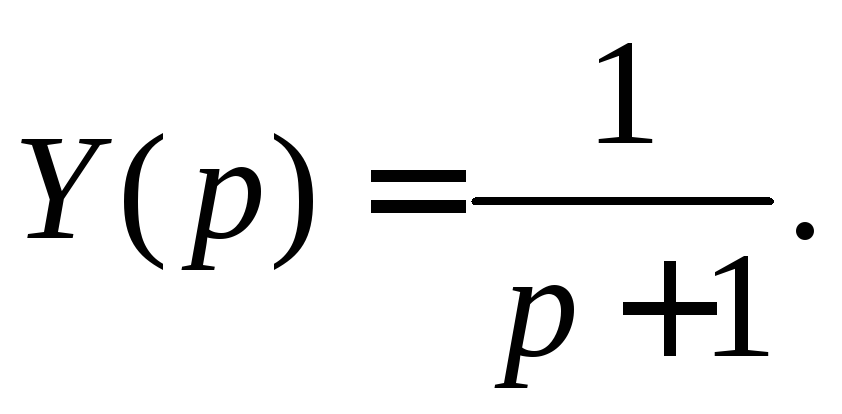
Тогда по таблице изображений находим

Замечание. Аналогично, используя теорему об интегрировании оригинала, можно решать интегральные уравнения, т.е. когда в уравнении искомая функция находится под знаком интеграла.

Пример 3. Найти решение интегрального уравнения

.

Переходим к изображениям:

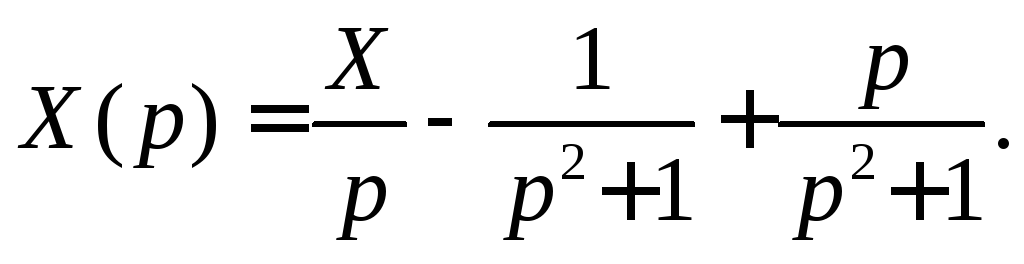
Из полученного уравнения определяем

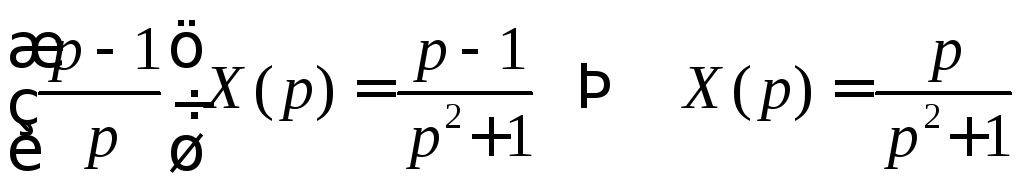
и по таблице изображений находим .