4.2. Основная теорема Коши

Теорема 2. Если однозначная и аналитическая функция в одно-связной области, то для любой замкнутой линиивыполняется

Представим интеграл в виде

и воспользуемся тем, что выражения из условий Коши – Римана являются полными дифференциалами. Тогда интеграл по замкнутой линии равен нулю, что и требовалось доказать.

Замечание 3. Верно и обратное утверждение (теорема Морера), т.е. если

то  аналитическая функция.

На основании этой теоремы легко доказать следующую теорему.

Теорема 3 (теорема Коши для сложного контура). Если функция однозначная и аналитическая в многосвязной областиD, то выполняется

М

N

А

B D

Рисунок приведен для случая трехсвязной области. Для доказатель-ства данной теоремы необходимо сделать разрезы АВ и МN, а затем применить основную теорему Коши для полученной односвязной области.

Лекция № 73

4.3. Интегральная формула Коши

Теорема 1. Если однозначная и аналитическая функция в областис границейL, то выполняется

(1)

Правая часть в формуле (1) называется интегралом Коши.

Пример 1. Вычислить интеграл .

4.4. Производные высших порядков от аналитической функции

Теорема 2. Однозначная и аналитическая функция в областиимеет в этой области производные всех порядков, которые определя-ются по формуле

(2)

где .

Доказательство формулы (2) следует из интегральной формулы Коши путём дифференцирования под знаком интеграла, что возможно в силу аналитичности подынтегральной функции .

С помощью формулы (2) можно вычислять некоторые интегралы.

Пример 2. Вычислить интеграл , где .

.

4.5. Ряд Тейлора

Аналогично, как и для функций действительной переменной, аналити-ческую функцию внутри круга сходимости можно представить сходящимся степенным рядом

(3)

где .

Тогда из формулы (2) получаем

. (4)

Определение 1. Степенной ряд (3), у которого коэффициенты опреде-ляются по формулам (4), называется рядом Тейлора для функции .

Определение 2. Если , то точканазывается нулем функции, а ряд Тейлора в окрестности этой точки имеет вид

.

Если к тому же , а, то точканазываетсянулем m-го порядка функции . В окрестности нуляm-го порядка аналитическая функции имеет вид

,

где .

Замечание. Ряды Тейлора для основных элементарных функций были приведены в лекции 71.

Пример 3. Разложить в ряд Тейлора функцию 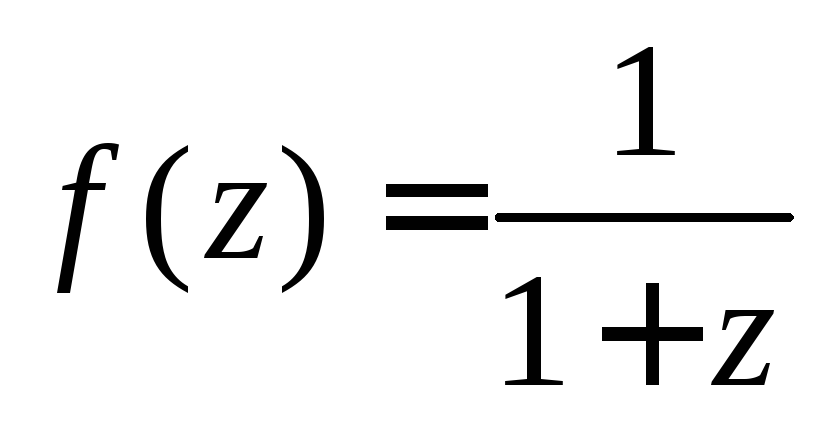в окрест-ности точки.

. . . . .

Тогда

,

где .

Легко заметить, что данная функция является суммой бесконечно убывающей геометрической прогрессии со знаменателем q = z.

4.6. Ряд Лорана

Определение 3. Ряд вида

называется рядом Лорана.

Его можно представить в виде

(5)

Первая сумма в правой части формулы (5) называется правильной частью, а вторая сумма – главной частью ряда Лорана.

Очевидно, областью сходимости ряда Лорана является общая часть областей сходимости его главной и правильной частей. Определим её.

Правильная часть сходится в области вида . Для главной части сделаем замену. Областью сходимости такого ряда является круг. Тогда главная часть сходится приили. Отсюда следует вывод:

1. Если , то область сходимости кольцо и при этом возможны случаи:

1.1.  кольцо (круг с выколотым центром);

1.2.  кольцо (вне круга);

1.3.  кольцо (плоскость с выколотой точкой).

2. Если  ряд Лорана не сходится ни при каких z.

Рассмотрим обратную задачу: Пусть задана аналитическая функция в кольце, тогда имеет место

Теорема 3. Функция аналитическая в кольце однозначно представляется рядом Лорана

, (6)

где

a контур L  окружность, принадлежащая кольцу, с центром в точке .

Пример 4. Разложить в ряд Лорана функцию в окрест-ности точки.

Представим функцию в виде суммы.

Последнее слагаемое в правой части уже является членом ряда Лорана. Разложим в ряд Лорана первое слагаемое:

.

Таким образом, данная функция у

в кольце разлагается

в ряд Лорана вида

О 1 х

. (7)

Найдем коэффициенты ряда Лорана также непосредственно по фор-муле (6):

Тогда ряд Лорана будет иметь вид (7).