Лекция № 72. Тема 3 : Производная функции комплексной переменной

3.1. Определение производной

Пусть функция определена в некоторой окрестности точкиz.

Определение 1. Если существует предел ,

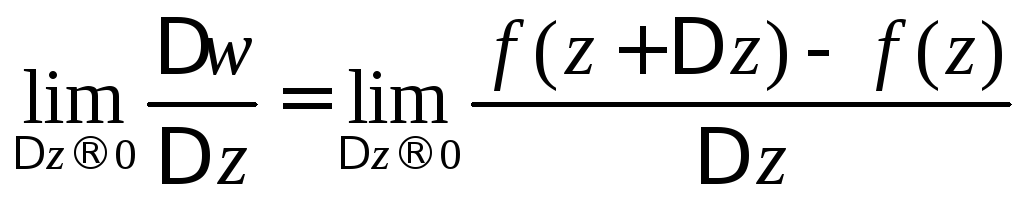то он называется производной функции и обозначаетсяили, а функцияназывается дифференцируемой.

Теорема 1. Если функция определена в неко-торой окрестности точкии функциииимеют непрерывные частные производные, то функциябудет дифферен-цируемой, если

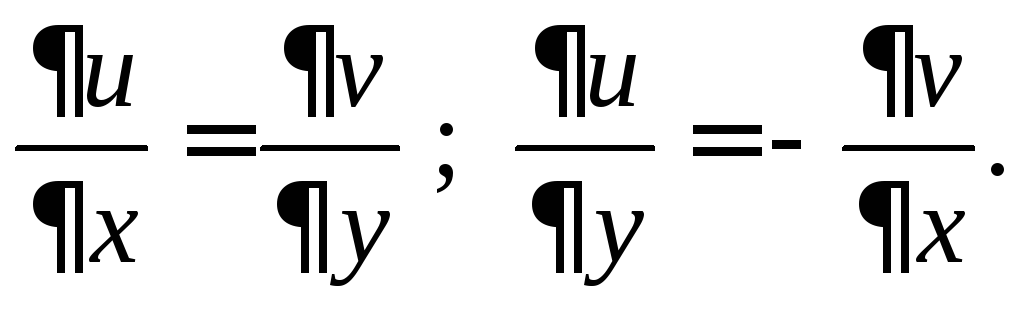(1)

Верно и обратное.

Условия (1) называются условиями Коши – Римана.

Пусть существует предел .

Так как этот предел не зависит от пути, по которому , то полагая, получаем

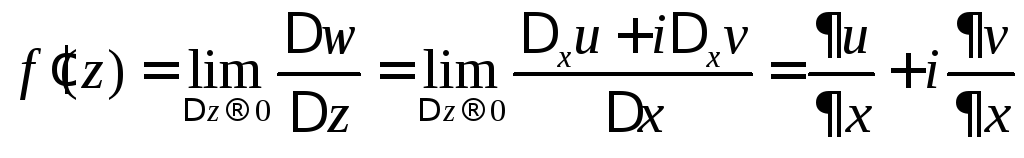. (2)

Аналогично, полагая , имеем

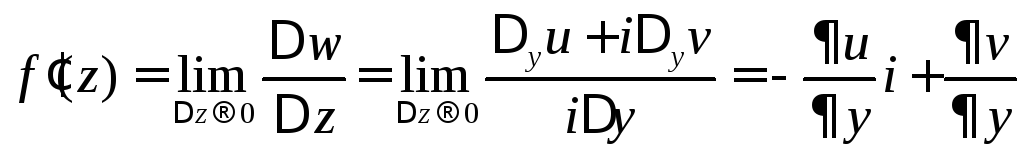. (3)

Сравнивая формулы (2) и (3), получаем условия (1).

Обратная часть теоремы. Пусть выполняются условия (1).

,

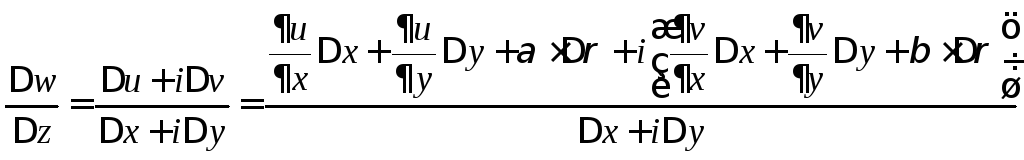где при.

Преобразуем это выражение с учётом формул (1)

,

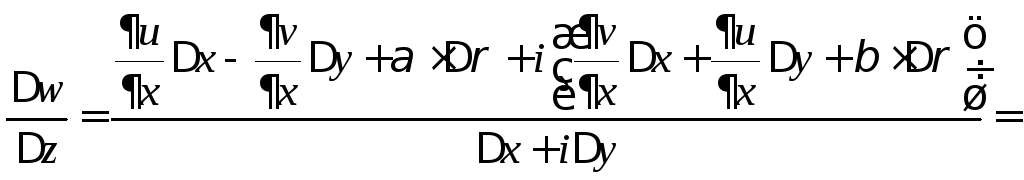
где при. Это означает, что предел существует и равен

.

Замечание 1. Из определения производной следует, что правила диф-ференцирования функции комплексной переменной такие же, как для функции действительной переменной.

3.2. Гармонические функции

Определение 2. Функция комплексной переменной дифференцируемая в точке и в некоторой ее окрестности называется аналитической.

Пример 1. Показать, что функция является аналитической и найти её производную.

и тогда

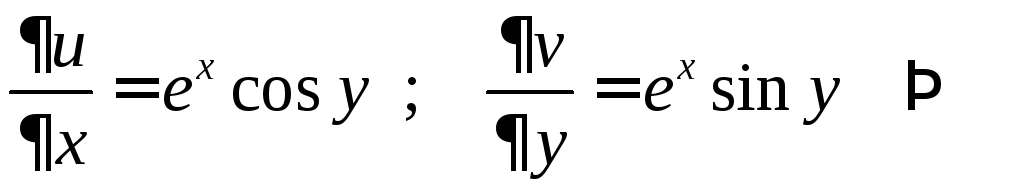
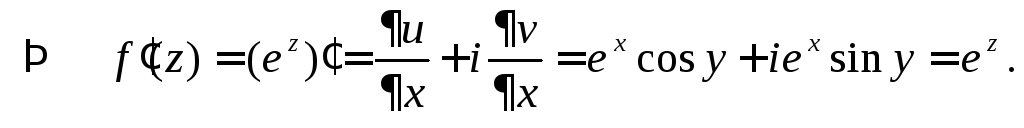
Замечание 2. Аналогично можно показать, что таблица производных для функций комплексной переменной такая же, как и для функций действительной переменной.

Из условий Коши – Римана можно получить уравнения, которым удовлетворяют функции и. Продифференцировав первое условие поx, а второе – по y и сложив полученные результаты, получим

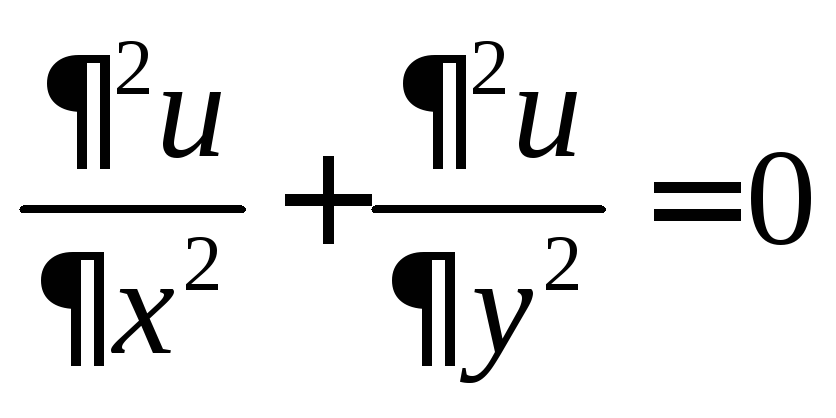и аналогично 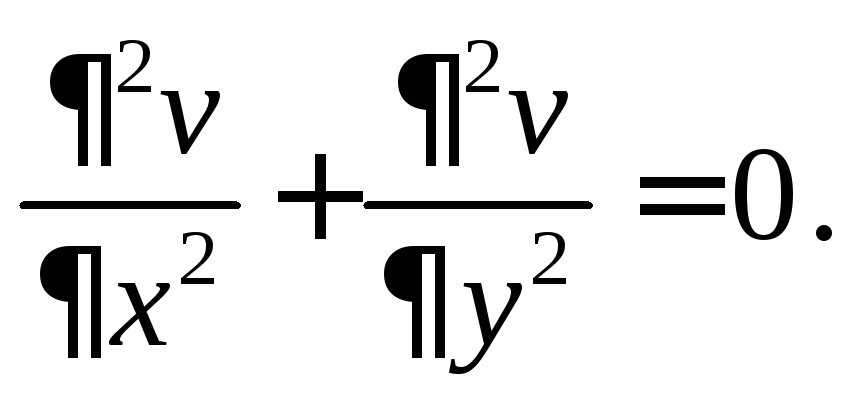 (4)

Определение 3. Функции, которые удовлетворяют уравнениям (4), называются гармоническими.

Если известна одна из функций или, то другую можно определить. Пусть известна, например, функция, тогда

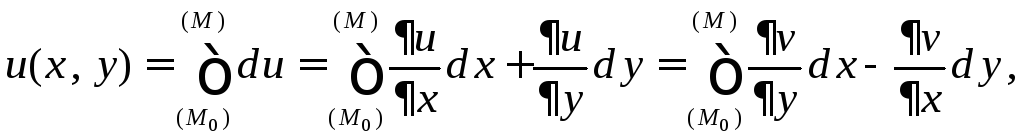
где - произвольная точка, а- фиксированная.

Пример 2. По действительной части аналитической функциивосстановить мнимую часть.

Имеем

В качестве пути интегрирования выберем ломаную, звенья которой параллельны координатным осям, тогда

где C - произвольная постоянная. Если задать условие , то, что определяет функцию

Тема 4 : Интеграл от функции комплексной переменной

4.1. Определение интеграла

Пусть на некоторой линии L задана непрерывная функция . Разобьём кривую L на п частей y B

. В каждой части

разбиения произвольно выберем

точку и составим интегральнуюL

сумму

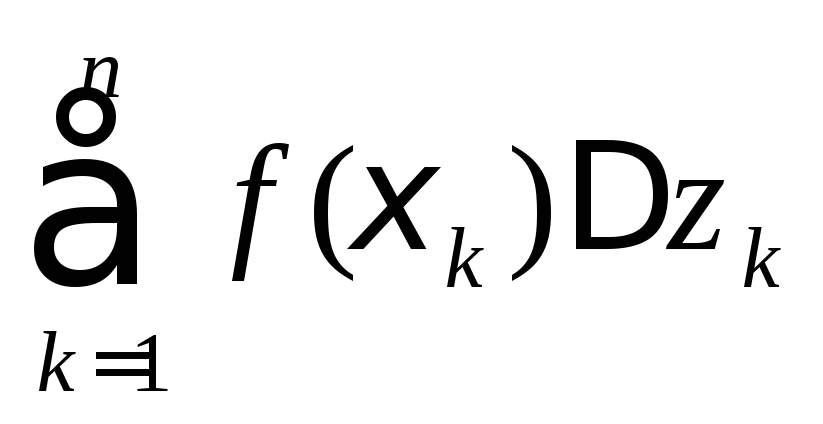. A

Тогда O x

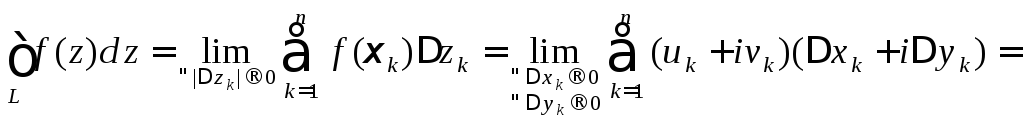
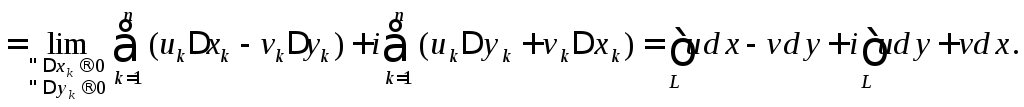
Таким образом, вычисление интеграла от функции комплексной переменной сводится к вычислению двух криволинейных интегралов от функций идействительных переменных. Из этого следует факт существования интеграла и его основные свойства:

1. Если

2. 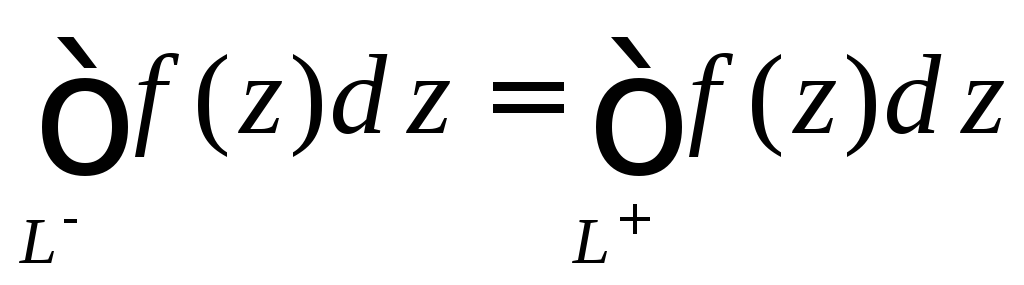, т.е. при изменении направления пути инте-грирования интеграл меняет знак;

3. Если выполняется

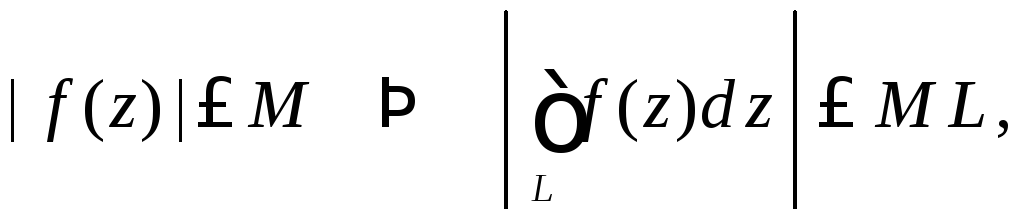
где L  длина линии.

Аналогично происходит и вычисление интеграла. Если линия

,

т.е. и тогда

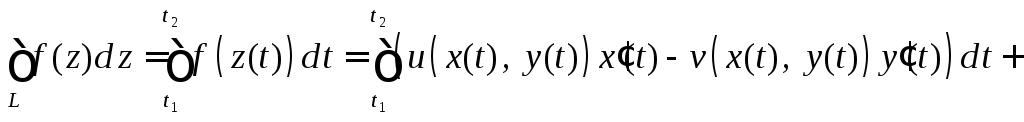
Пример 3. Вычислить 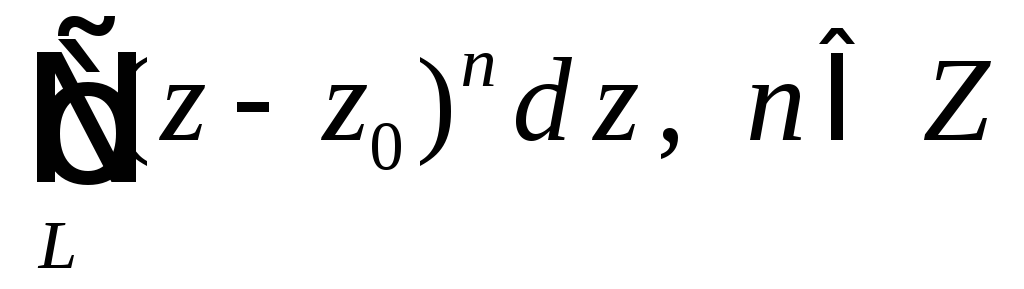, где контуром является окружностьL :

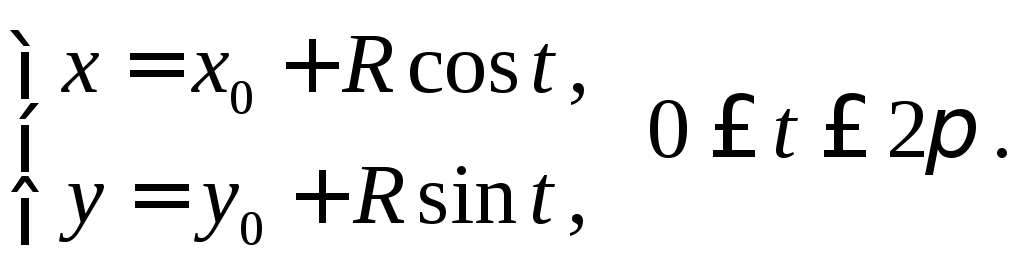
Представим уравнение окружности в комплексной форме

,

тогда

.
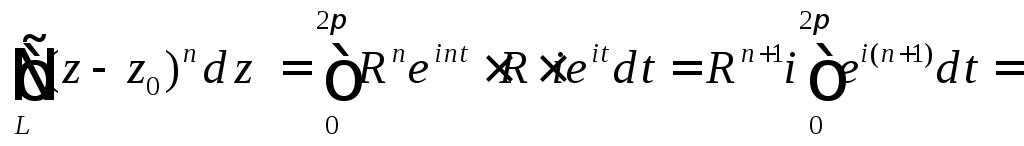
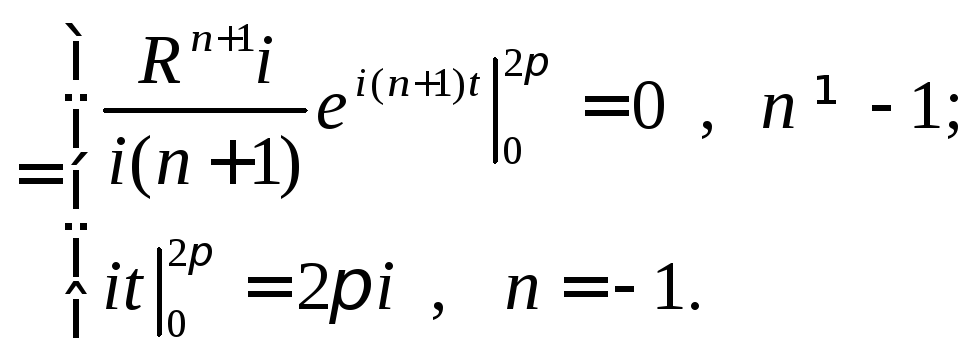