КДМ / Lektsii-DM

14

1.9 Завдання для самостійної роботи

1.Задано множини X,Y,Z,U .

X– множина букв, що має ім'я студента;

Y– множина букв по батькові студента;

Z– множина букв прізвища студента;

U – універсальна множина U X Y Z {голосні, що відсутні в множинах X, Y, Z}.

1.1 Обчислити множини:

– X Y, X Z,Y Z, X Y Z ;

–Y Z, X Y Z, X \ Z,Z \ X,X Z, X Z ;

–X Y, X (Y Z),(X \ Z) (Z \ X);

1.2Намалювати діаграми Ейлера для множин:

–X Y Z ;

–(X Y) Z ;

–(X \ Z) (Y \ Z) .

1.3Перевірити експериментально на множинах X, Y, Z справедливість наступних тверджень:

–(X Y) X Y ;

–(X Y) X Y ;

–X \ (Y Z) (X \ Y) (X \ Z);

–X \ (Y Z) (X \ Y) (X \ Z).

1.4Для довільної підмножини множини Z потужності 4 скласти булеан, навести три приклади покриття та перелічити усі розбиття.

2. Довести наступні тотожності, використовуючи відношення належності. Продемонструвати на колах Ейлера:

–A (B C) (A B) (A C) ;

–A (B C) (A B) (A C) ;

–A \ (B C) (A \ B) (A \ C) ;

15

–A \ (B C) (A \ B) (A \ C) ;

–A \ (A \ B) A B ;

–A \ B A \ (A B) ;

–A (B \ C) (A B) \ (A C) (A B) \ C ;

–(A \ B) \ C (A \ C) \ (B \ C);

–(A B) (A B) (A B) (A B) A ;

–(A B) A A B ;

–(A B) \ C (A \ C) (B \ C) ;

–A \ (B \ C) (A \ B) (A C) ;

–A \ (B C) (A \ B) \ C ;

–A (B C) (A B) C .

3.Визначте істинність або хибність кожного з наступних тверджень:

; ; ; A ; A , де A - довільна множина.

4.Визначте істинність або хибність кожного з наступних тверджень:

а) {9} 1, {3, 5}, 7, {9} ;

б) 5 1, 3, 5, {7}, 9 ;

в) 1, 3, 5 1, 2, {3}, 4, 5 ; г) 1, 3, 5 1, 2, 3, 4, 5 ;

д) 1, 4, 5 1, 2, {3}, 4, 5 .

5. Визначте потужність та запишіть булеан для кожної наступної множини:

а) , 1, 2, 3, 4, 5 ;

б) 1, {2}, 3, 4, 5, 6,7 ; в) 1, 2, 3, 4, 5, 6, 7 ;

г) 1, 2 , 3, 4 , 5 , 6, 7 .

6. Для кожної з наведених нижче множин використайте діаграми Ейлера і заштрихуйте та її частини, які зображують задані множини:

7. Для аналізу попиту населення на кондитерську продукцію було проведено опитування серед населення. Із 1000 респондентів 560 купують продукцію вітчизняного виробництва, 390 - імпортного, 100 - як вітчизняного, так і імпортного виробництва.

За допомогою діаграм Ейлера визначити кількість опитуваних, що купують продукцію:

1)тільки вітчизняного виробництва;

2)тільки імпортного виробництва;

3)взагалі не купують кондитерські вироби.

1.10Контрольні питання

1.Дати визначення множини.

2.Способи завдання множини.

3.Привести приклади скінченних та нескінченних множин.

4.Дати визначення порожньої й універсальної множин.

5.Дати визначення тотожно рівних множин.

6.Що називають підмножиною множини?

7.Чим відрізняються поняття включення й строге включення?

8.Визначити поняття булеану.

9.Сформулювати теорему про потужність булеану.

10.Визначити основні операції над множинами.

11.Графічний метод завдання множини. Кола Ейлера.

12.Записати основні закони алгебри множини.

13.Що таке розбиття та покриття множини. Навести приклади.

17

РОЗДІЛ 2 ТЕОРІЯ ВІДНОШЕНЬ

2.1 Основні визначення теорії відношень Кортеж, набір, вектор – упорядкована послідовність елементів, у якій

кожен елемент займає певне місце.

Елементи, що утворюють кортеж, називаються координатами або компонентами кортежу (вектора). Кількість координат кортежу називається

довжиною або розмірністю кортежу.

( ) – порожній кортеж, (x) – одноелементний кортеж, (x, y) – пара, двоелементний кортеж, (x1, x2 ,..., xn ) – кортеж довжини n або n-ка ( "енка").

Прямий (декартовий) добуток множин Х та Y – множина усіх упорядкованих пар елементів (x,y) таких, що перший елемент належить першій множині, тобто X , а другий елемент належить другій множині, Y :

X Y {(x,y) | x X, y Y}.

Прямий (декартовий) добуток n множин X1, X2 ,..., Xn – множина усіх упорядкованих наборів (x1 ,x2 ,...,xn ) таких, що перший елемент належить множині X1 , другий – множині X2 , …, n -й – множині Xn :

X1 X2 ... Xn (x1 , x2 ,..., xn ) x1 X1 , x2 X2 , ..., xn Xn .

Декартовий добуток X X називається декартовим квадратом множини X та позначається X2.

Декартовий добуток X X ... X , у якому одна й та ж множина X

n

перемножується n разів сама на себе називається декартовим степенем множини X : Xn .

Наприклад.

Нехай X x, y , Y 1,2 , тоді

X Y (x,1), (x,2), (y,1), (y,2) , а Y X (1, x), (1, y), (2, x), (2, y) .

18

R R R2 – множина точок декартової площини;

R R ... R Rn – множина точок n -мірного простору. Шахматна дошка:

X a, b, c, d, e, f , g, h , Y 1,2,3,4,5,6,7,8 , X Y (a,1),...,(h,8) .

Властивості декартова добутку множин:

1)X Y Y X;

2)X Y X Y ;

3)X (Y Z) (X Y) (X Z);

4)X (Y Z) (X Y) (X Z).

n - арне або n -місне відношення R на множинах X1, X2 ,..., Xn – це всяка, довільна підмножина декартова добутку цих множин:

R X1 X2 ... Xn .

Якщо набір елементів (x1, x2 ,..., xn ) належить відношенню R , то кажуть,

що елементи (x1, x2 ,..., xn ) знаходяться у відношенні R або пов’язані

відношенням R .

n -арне або n -місне відношення R на множині X – це всяка, довільна підмножина n -го декартова степеня цієї множини: R Xn .

При n 1 маємо унарні або одномісні відношення.

При n 2 маємо бінарні або двомісні відношення, які використовуються найбільш часто, і тому позначаються малими грецькими літерами на відміну від n -арних відношень, що позначаються великими латинськими літерами (як множини).

Бінарне відношення на множинах X і Y – це всяка, довільна підмножина декартова добутку цих множин:

X Y {(x,y) | x X, y Y}.

Якщо X2 , то кажуть, що відношення задане на множині Х.

Якщо елемент (x,y) належить відношенню , то кажуть, що пара (x,y)

знаходиться у відношенні чи зв'язана відношенням : (x,y) чи x y .

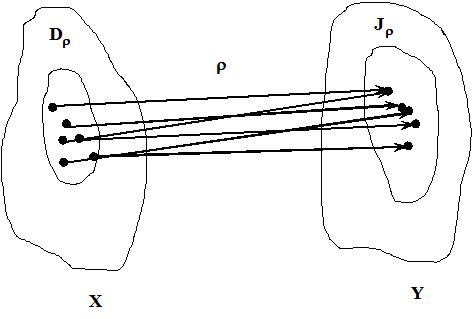
19

Область визначення D бінарного відношення – множина перших координат кожної впорядкованої пари, що належить відношенню :

D { x|(x,y) }.

Область значень J бінарного відношення – множина других координат кожної впорядкованої пари, що належить відношенню :

J { y |(x,y) } .

У загальному випадку область визначення відношення не співпадає з множиною X : D X та область значення відношення не співпадає з множиною Y : J Y.

2.2Способи завдання бінарних відношень

1)Перелік пар або завдання характеристичної властивості

Довільне бінарне відношення (як множину) задають у вигляді переліку усіх упорядкованих пар, із яких складається відношення, або з використанням характеристичної чи визначальної властивості.

Наприклад.

, X2 , X {1,2,3,4}.

20

{(x,y) | x,y X, x y} {(1,1),(2,2),(3,3),(4,4)}.

{(x,y) | x,y X, x y}

{(1,1),(1,2),(1,3),(1,4),(2,2),(2,3),(2,4),(3,3),(3,4),(4,4)}

2) Матриця відношення

У матриці відношення рядки відповідають елементам множини X, стовбці елементам множини Y, елемент матриці дорівнює:

Якщо X n, Y m , тоді матриця відношення має розмір: n m.

Наприклад.

Матриця відношення має вигляд A :

3)Графічне зображення відношень

Існує декілька варіантів графічного зображення відношень.

21

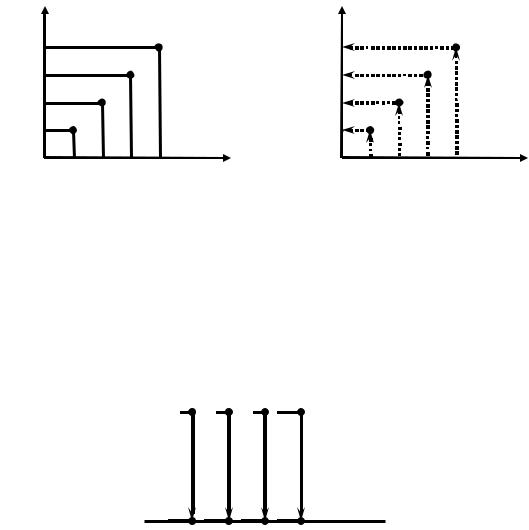
По-перше, відношення може бути зображено у декартовій системі координат. На кожній осі відкладаються елементи множин X і Y , наприклад, вісь Ox – елементи множини X , вісь Oy – елементи множини Y . Якщо пара (x,y) , на площині буде зображено точку із координатами (x,y) .

Наприклад.

Графічне зображення відношення у декартовій системі координат.

По-друге, відношення може бути зображено із використанням двох паралельних, вертикальних або горизонтальних відрізків прямих.

Наприклад.

Графічне зображення відношення у такий спосіб.

Y

1 2 3 4

По-третє, відношення може бути зображено у вигляді орієнтованого графу. На площині зображуються точками елементи множин X і Y .

Якщо пара (xi ,yj ) належить відношенню, то дугою з’єднуються точки, які відповідають парі (xi ,y j ), причому дуга направлена від першого елемента до другого.

22

Позначаючи таким чином усі пари, що належать відношенню, отримаємо фігуру, яка називається графом відношення.

Графічне зображення відношення:

{(1,5),(2,4),(3,6),(6,2)} на Х, X2 , X {1,2,3,4,5,6}.

2.3 Екстремальні відношення

Для довільної множини X:

Ix (x,x) x X – тотожне відношення;

Ux X2 – універсальне відношення;

X2 – порожнє відношення. Наприклад.

Нехай X {1,2,3}, тоді Ix (1,1),(2,2),(3,3) ; x ; Ux (1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3) .

2.4 Операції над відношеннями

Оскільки бінарні відношення є множинами над ними визначені усі операції, які були введені для множин, тобто перетин, об'єднання та інші. Але для бінарних відношень існують й специфічні операції, це обернення та композиція.

Нехай – деяке бінарне відношення.

Обернене відношення 1 до відношення визначається як:

1 (y,x) (x,y) .

Обернене відношення утворюється за рахунок перестановки значень у кожній упорядкованій парі прямого відношення .