
КДМ / Lektsii-DM
.pdf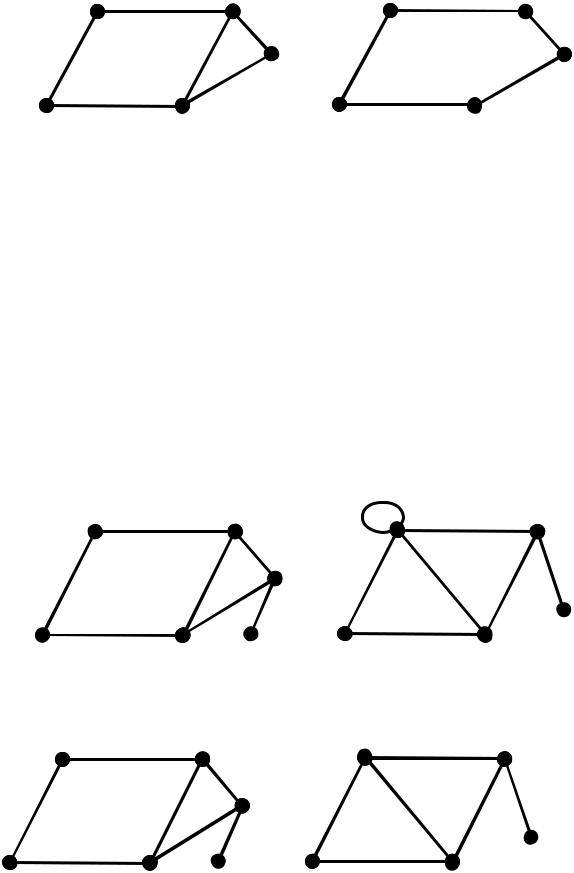
|
|
|
|
|
|
|
143 |
|
G |
|
|
|
|
G \ e4 |
|
V1 |
e2 |
|
V2 |
V1 |
|
e2 |
V2 |
|
|
|
|
|
|
||
e1 |
|
e4 |
e6 |
e1 |
|
|
e6 |
|
V5 |
|
|
V5 |
|||
|
|
|
|
|
|
||
|
|
|
e5 |
|
|
|
e5 |
V3 |
e3 |
V4 |
|
V3 |
e3 |
V4 |
|
|
|
|
|
||||
|
Замикання або ототожнення вершин |
|
|||||
Пара вершин vi |
та vj у графі G замикається, якщо вони замінюються |
||||||
такою новою вершиною u (або остається позначка однієї із вершин), що всі ребра графа G інцидентні вершинам vi та vj , стають інцидентними цій новій вершині u .
Стягування
Стягування ребра e = {u, v} означає ототожнення його суміжних вершин
uта v .
1)Ілюстрація операції замикання вершин v1 та v2 .
V1 |
V2 |
V1 |
V5 |
|
|
V5 |
|
V6
V3 |
V4 |
V6 |
V3 |
V4 |
2) Ілюстрація операції стягування ребра {v1 , v2 }. |
|
|||
V1 |
|
V2 |
V1 ≡ V2 |
V5 |
|
|
V5 |
|
|
V6
V3 |
V4 |
V6 |
V3 |
V4 |
144
5.12 Завдання для самостійної роботи
1. Відновити граф за матрицею інцидентності. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
2 |
0 |
1 |
0 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
3 |
1 |
0 |
0 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
4 |
1 |
0 |
1 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
2. Відновити граф за матрицею суміжності. Побудувати матрицю
інцидентності. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
1 |
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
0 |
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
1 |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
0 |
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
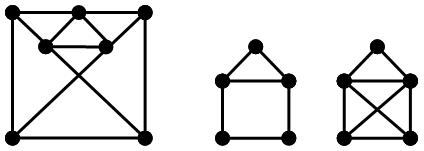
3. Визначити ізоморфну вкладеність графів G2 ,G3 |
у G1 . |
|||||||
|
|
|
|
|
|
|
|
|
|
|
G1 |
|
|
G2 |
|
G3 |
|
4. Для графа G знайти:
а) найбільший Кр, Оn, изоморфно-вкладені в G; б) найбільшу зірку, изоморфно-вкладену в G.
145
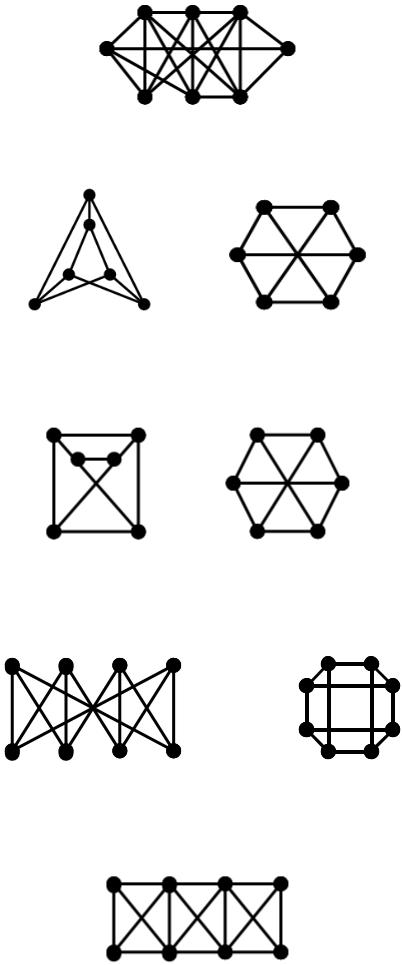
5. Визначити та довести ізоморфізм наступних графів.
6. Визначити та довести ізоморфізм графів.
7. Визначити та довести ізоморфізм графів.
8. Привести усі максимальні та найбільші незалежні множини графа. Знайти число незалежності.
146
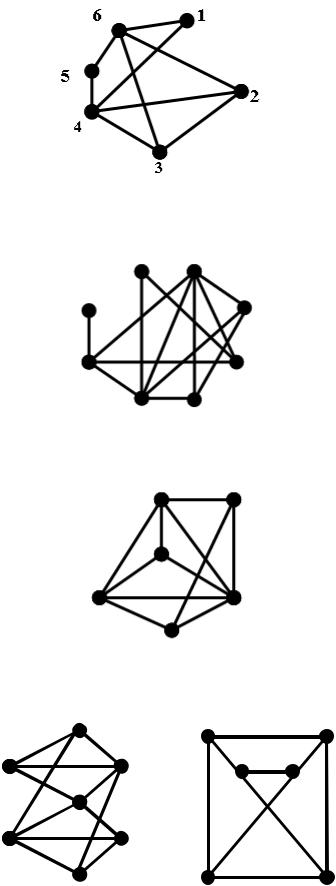
9. Привести усі максимальні та найбільші незалежні множини графа. Знайти число незалежності.
10.Привести усі кліки графа максимальні та найбільші G . Знайти клікове
число.
11.Привести усі кліки графа максимальні та найбільші G . Знайти клікове
число.
12.Визначити, чи є наступні графи дводольними, тридольными або регулярними?
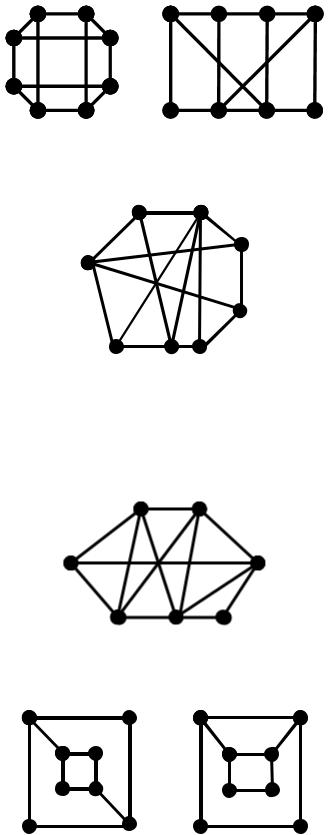
147
13.Визначити, чи є наступні графи дводольними, тридольными або регулярними?
14.Визначити всі найменші та мінімальні домінуючі множини графа. Визначити число домінування.
15. Визначити всі найменші та мінімальні домінуючі множини графа. Визначити число домінування.
16. Визначити ізоморфні чи ні наступні графи. Відповідь обґрунтувати.
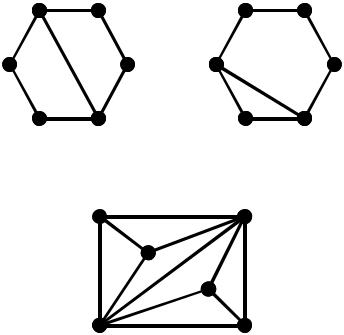
148
17. Привести усі кліки графа максимальні та найбільші G . Знайти клікове число.
5.13Контрольні питання
1.Що таке неорієнтовані граф?
2.Визначення підграфа, остовного і породженого підграфа. Доповнення
графа.
3.Ізоморфізм графів. Ізоморфна вкладеність.
4.Помічені і абстрактні графи. Повні, порожні, дводольні та регулярні графи. Простий, псевдограф та мультиграф. Зірка.
5.Ступені вершин графа. Лема про рукостискання. Ізольована та домінуюча вершини.
6.Незалежна множина. Максимальне і найбільша незалежна множина. Число незалежності.
7.Кліка. Максимальна і найбільша кліка. Клікове число або щільність
графа.
8.Домінуюча множина. Мінімальна та найменша домінуюча множина. Число домінування.
9.Обчислити число ребер в повному графі. Обчислити число різних помічених p -графів, число різних помічених (p,q)-графів.

149
РОЗДІЛ 6 МАРШРУТИ І ЗВ'ЯЗНІСТЬ У НЕОРІЄНТОВАНИХ ГРАФАХ
6.1 Види маршрутів неорграфів
Маршрут M (v0 ,e1 , v1 ,e2 ,...,en , vn ) неорієнтованого графу G (V,E) –
скінченна послідовність вершин та ребер, що чергуються, починається й закінчується вершиною, кожне ребро маршруту з’єднує дві вершини маршруту
– попередню та наступну.
Кінцеві вершини маршруту – v0 та vn , внутрішні – всі інші вершини. Маршрут неорграфа повністю задається переліком вершин або/і ребер, в
той же час, якщо треба тільки підкреслити, що маршрут починається у вершині v0 , а закінчується vn маршрут позначається, як: M (v0 , vn ) або
M (v0 vn ) .
Замкнутий маршрут M (v0 , vn ) – кінцеві вершини співпадають
(v0 vn ) , інакше – відкритий (v0 vn ) .
Ланцюг – маршрут, усі ребра якого розрізняються (крім можливо кінцевих).
Простий ланцюг – маршрут, усі вершини якого (крім можливо кінцевих), а отже і ребра, розрізняються.
Цикл – замкнутий ланцюг.
Простий цикл – замкнутий простий ланцюг, n 3 , n – кількість вершин. Позначення: Cn – простий цикл, n 3 , n – кількість вершин.
Pn – простий ланцюг, n – кількість вершин.
C3 P5

150
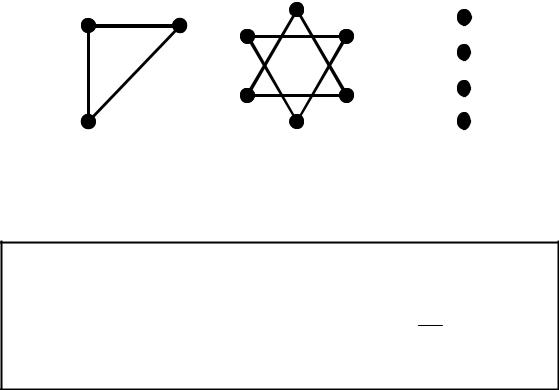
Наприклад.
Наведений граф G . Навести приклади маршруту, ланцюга, простого ланцюга, замкнутого маршруту, циклу і простого циклу.
1 |
2 |
|
3 |
||
|
||
|
4 |
|
7 |
|
|
|
5 |
|
6 |
|
Маршрут M1 (1,4,5,3,7,2,4,5,6). Для маршруту M1 вершини 1 та 6 – кінцеві; 2,3,4,5,7 – внутрішні.
Маршрут M1 – відкритий, не ланцюг і не простий ланцюг (ребро {4,5} повторюється).
Маршрут M2 (1,4,5,3,7 ,2,4,5,6,1 ) .
Маршрут M2 – замкнутий, не цикл і не простий цикл (ребро {4,5} повторюється).
Маршрут M3 (3,7,6,3,2,5).
Маршрут M3 – не простий ланцюг (вершина 3 повторюється ).
Маршрут M4 (3,7,6,3,2,5,3) .
Маршрут M4 – не простий цикл (вершина 3 повторюється).
Маршрут M5 (1,4,5,3,6 ,7,2) . Маршрут M5 – простий ланцюг. Маршрут M6 (1,4,5,6,7,1). Маршрут M6 – простий цикл.
Твердження
Усякий (u,v)- маршрут містить простий (u,v)- ланцюг. Усякий цикл містить простий цикл.
151
6.2 Зв'язність у неорграфах
Зв'язний неорієнтований граф G – будь-яка пара вершин з'єднана маршрутом (простим ланцюгом) в G .
Компонента зв'язності або компонента неорграфа G – максимальний за включенням вершин зв'язний підграф графа G.
Дві вершини u та v називають зв'язаними у неорграфі G , якщо в G існує (u, v) -маршрут.
Кожна вершина неорграфа вважається зв'язаною сама із собою.
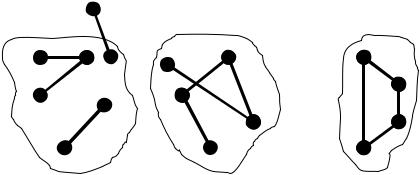
Наприклад.
На рисунку зображені три графи. Перший з них являється зв'язним, складається із однієї компоненти зв'язності. Другий складається із двох компонент зв'язності (два трикутники), тому є незв’язним. Третій граф не є зв’язним, має у своєму складі чотири компоненти.
Теореми про зв’язні графи Теорема 1
Будь-який неорграф G може бути представлений, як об'єднання своїх непересічних компонент зв'язності:
k
G Gi , Gi Gj , i j, i, j 1,k
i 1
Доведення.
Дано граф G (V,E). Визначимо на множині його вершин V наступне бінарне відношення . Дві довільні вершини u та v графу G находяться у
152
відношенні , якщо існує (u, v) - маршрут у графі G або ці вершини є зв’язаними у графі G .
Відношення зв'язності вершин є відношенням еквівалентності: 1) рефлексивно:
v V |
v v ; |
2) симетрично: |
|
u, v V |
u v v u , |
u v M (u,e1 ,....,en , v)M (v,en ,....,e1 ,u) v u ; 3) транзитивно:
u, v, w V u v, v w u w , u v M1 (u, e11 ,....e1n , v) , v w M2 (v, e12 ,....,em2 , w)
M M1 M2
(u, e11 ,...,e1n , v, e12 ,...,em2 , w) u w.
Відношення є відношенням еквівалентності, отже, воно задає розбиття
множини |
вершин |
V |
графу на класи |
еквівалентності: V V1 ... Vk, |
|||||
i, j |
|
|
i j |
Vi Vj , Vi V. Тоді, породжені підграфи на множинах Vi і |
|||||
1,k |
|||||||||
тільки вони являються, за визначенням, компонентами зв'язності графа G , тому |
|||||||||
k |
|
|
|
|
|
|
|
||
G Gi |
, Gi |
G j |
, i j, i, j |
1,k |
, що й треба було довести. |
||||
i 1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
v1 |
|
v2 |
vk |
|
…
G1 |
G2 |
Gk |
