КДМ / Lektsii-DM

163

Покласти l(i) для всіх i s та вважати ці позначки тимчасовими. Покласти p s .

Крок 2.

Для всіх i (p), позначки яких тимчасові, замінити позначки відповідно до наступного виразу:

l(i) min[ l(i), l(p) c(p,i) ].

Крок 3.

Серед усіх вершин із тимчасовими позначками знайти таку, для якої: l(i ) min[l(i)]

Крок 4. Вважати позначку вершини i постійною і покласти p i .

Крок 5.1.

Виконується, якщо треба знайти найкоротший шлях тільки від s до t . При p t алгоритм закінчує роботу, l(p) є довжина найкоротшого шляху

від s до t .

При p t перейти до кроку 2.

Крок 5.2.

Виконується, якщо треба знайти найкоротший шлях від s до усіх інших вершин графу.

Якщо усі вершини отримали постійні позначки, то алгоритм закінчує роботу.

Якщо деякі вершини мають тимчасові позначки, перейти до кроку 2.

Як тільки довжини найкоротших шляхів будуть знайдені, самі шляхи можна отримати за допомогою рекурсивної процедури з використанням співвідношення:

l(i ) c(i ,i) l(i) .

Оскільки вершина i безпосередньо передує вершині i в найкоротшому шляху від s до i , то для будь-якої вершини i відповідну вершину i можна знайти як одну з вершин, що залишилися, для якої виповнюється: l(i ) c(i ,i) l(i) .

164

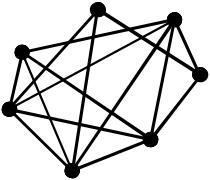
Наприклад.

Граф G : постійні позначки будемо виділяти знаком .

вважаємо її постійною. p 1.

Встановлюємо тимчасові позначки для вершин (2,...,7). l(2) l(3) ... l(7) .

Крок 2. (p) (1) {3,5,6,7} – усі вершини, суміжні вершині 1 мають тимчасові позначки.

Змінюємо тимчасові позначки відповідно до виразу l(i) min[ l(i), l(p) c(p,i) ]:

165

l(3) min( ,0 4) 4

l(5) min( ,0 15) 15

l(6) min( ,0 13) 13

l(7) min( ,0 1) 1

Шаг 3. l(i ) min ( 4, 15 , 13 , 1, ) 1 , відповідає вершині i 7 .

3 5 6 7 2 ,4

Крок 4. l(7) 1 – вершина 7 отримує постійну позначку. p 7 .

Крок 5. Не всі вершини мають постійні позначки, а тільки {1,7}, тому алгоритм продовжує роботу, переходимо до кроку 2.

Крок 2. (p) (7) {1,2,3,5,6}.

Серед них тільки вершина 1 має постійну позначку, тому перераховуємо

Крок 5. Не всі вершини мають постійні позначки, а тільки {1,3,7}, алгоритм продовжує роботу, переходимо до кроку 2 .

Крок 2. (p) (3) {1,4,5,6,7}.

Постійні позначки мають вершини {1,3,7}, виключаємо їх із розгляду, перераховуємо тимчасові позначки для вершин {4,5,6}:

l(4) min( , 3 9) 11 , l(5) min(12, 3 12) 12 , l(6) min(13, 3 13) 13 .

166

Крок 3. Серед усіх вершин із тимчасовими позначками, а це множина вершин {2,4,5,6}, знаходимо:

Крок 4.

l(2) 8 – вершина 2 отримує постійну позначку. p=2.

Крок 5. Не усі вершини мають постійні позначки, а тільки {1,2,3,7}, алгоритм продовжує роботу, переходимо до кроку 2.

Крок 2. (p) (2) {4,6,7} , вершина 7 має постійну позначку, тому виключаємо її із розгляду.

l(4) min(12, 8 4) 12 , l(6) min(13, 8 5) 13 ,

l(4) l(5) 12 , p 4, 5 .

Можна вибирати як вершину 4, так і вершину 5. Вибираємо вершину 4. l(4) 12 , p 4 .

Множина вершин із постійними позначками: {1,2,3,4,7}.

Крок 2. (p) (4) {2,3,5} , вершини 2 та 3 мають постійну позначку, отже, не розглядаються.

l(5) min(12, 12 3) 12,

l(i ) min ( 12 ,13 ) 12 , вершина 5 отримує постійну позначку. l(5) 12 , p 5 .

Множина вершин із постійними позначками: {1,2,3,4,5,7}.

Крок 2. (p) (5) {1,3,4,6,7} , усі вершини, окрім 6 мають постійні позначки.

l(6) min(13,12 2) 13 ,

l(6) 13 , p 6 .

Множина вершин із постійними позначками: {1,2,3,4,5,6,7}.

167

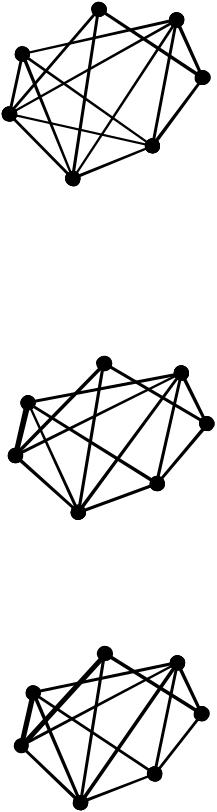
Крок 5. Усі вершини мають постійні позначки, алгоритм закінчує роботу. Знайдені найкоротші відстані від вершини 1 до всіх інших вершин у графі.

8 2

3 3

0 1

4 12

1 7

5 12

6 13

Таким чином, найкоротші маршрути від вершини 1:

1 - 7 (1,7) 1

2 3

1

4

7

5

6

1 - 2 (1,7,2) 8

2 3

1

4

7

5

6

168

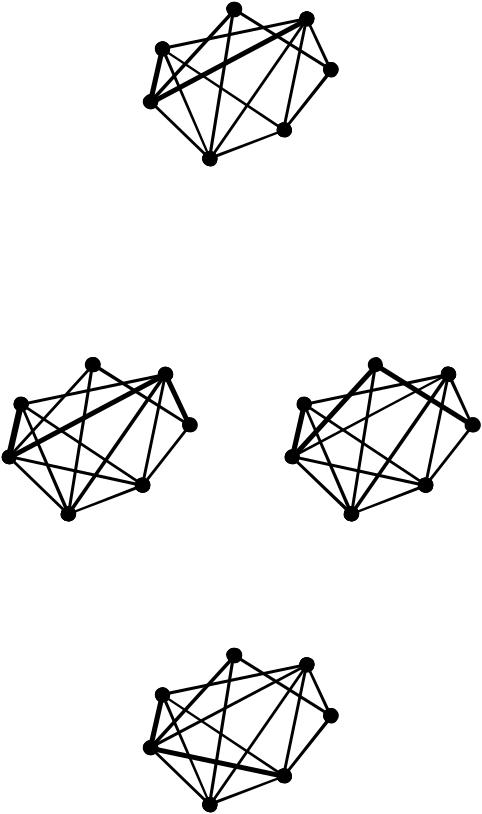
1 - 3 (1,7,3) 3

2 3

1

4

7

5

6

1 - 4 (1,7,3,4) (1,7,2,4) 12

1 - 5 (1,7,5) 12

2 3

1

4

7

5

6

169

Алгоритм Форда

Задача про найкоротший шлях полягає у знаходженні найкоротшого шляху від заданої початкової вершини s V до заданої кінцевої вершини t V , за умови існування такого шляху. Елементи cij матриці ваги C можуть бути позитивними, від’ємними або нулями.

Всі цикли в графі G мають невід’ємну сумарну вагу.

Нехай lk (i) – позначка вершини i в кінці (k 1) -й ітерації, (s) – множина вершин, суміжних із s . Алгоритм може бути легко модіфікований для застосування у орієнтованих графах.

Крок 1. Покладемо, S = Ã(s),k = 1, l1 (s) 0 , l1 (i) c(s,i) для усіх i (s)

та l1 (i) для всіх інших i .

Крок 2. Для кожної вершини i (s) , i s змінити її позначку наступним чином :

lk 1(i) min [lk (i), min {lk (j) c(j,i)} ], де Ti (i) S .

j Ti

Для кожної вершини i (s) покладемо lk 1 (i) lk (i) .

дорівнюють довжинам найкоротших шляхів.

цикл негативної ваги та задача не має рішення.

Крок 4. Відновити множину таким чином : S {i |lk 1 (vi ) lk (vi )}. Крок 5. Покласти k k 1 та перейти до кроку 2.

Алгоритм Флойда (найкоротші шляхи між усіма парами вершин)

Нехай потрібно знайти найкоротші шляхи між усіма парами вершин графа. Вочевидь, що можливо застосування попередніх алгоритмів із кожної вершини графа, але метод Флойда може бути застосовано для довільної матриці ваги. Метод базується на використанні послідовності з p перетворень (ітерацій) початкової матриці ваги C. При цьому на k -й ітерації матриця представляє довжини найкоротших шляхів між кожною парою вершин з тим обмеженням, що шлях між i та j (для будь-яких i та j) містить у якості проміжних тільки вершини з множини: {1,2,...,k}.

Всі цикли в графі G мають невід’ємну сумарну вагу. Крок 1. Покласти k 0 .

Крок 2. k k 1.

Крок 3. Для всіх i k , таких, що cik , та для усіх j k , таких, що ckj , вводимо операцію:

cij min[cij ,(cik cjk )].

Крок 4. Якщо cii 0,то в графі існує цикл від’ємної ваги, що містить вершину i , розв’язання задачі не існує.

Якщо все усі cii 0 та k p , то отримано рішення та матриця дає довжини всіх найкоротших шляхів.

Якщо все cii 0, але k p , то повернутися до кроку 2.

171

6.6 Завдання для самостійної роботи

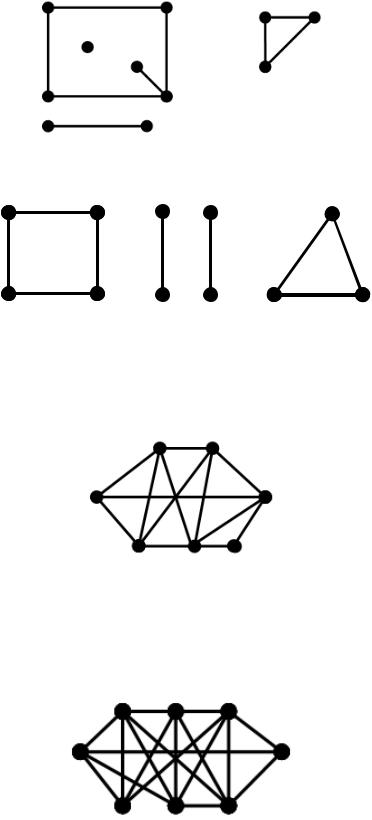
1. Визначити, чи є заданий граф зв'язним. Визначити кількість та виділити множини компонент зв’язності.

а)

б)

2.Для наступного графа виділити маршрут не ланцюг, замкнутий маршрут не ланцюг, ланцюг, простий ланцюг, цикл, простий цикл. Визначити обхват та оточення графу.

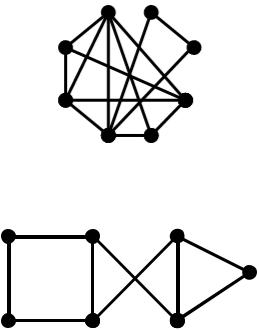
3.Для наступного графа виділити маршрут не ланцюг, замкнутий маршрут не ланцюг, ланцюг, простий ланцюг, цикл, простий цикл. Визначити числа вершинної та реберної зв’язності.

172

4.Для наступного графа визначити числа вершинної та реберної зв’язності. Знайти мости та вершини зчленування, визначити блоки графу.

5.Для наступного графа визначити числа вершинної та реберної зв’язності. Знайти мости та вершини зчленування, визначити блоки графу.

6.Навести приклад графа G , для якого:

(G) 1 – число вершинної зв’язності G ;(G) 2 – число реберної зв’язності G ;

(G) 3 – мінімальна степінь вершин графа G . 7. Навести приклад графа G , для якого:

(G) 2 – число вершинної зв’язності G ;(G) 3 – число реберної зв’язності G ;

(G) 3 – мінімальна степінь вершин графа G . 8. Навести приклад графа G , для якого:

(G) 3 – число вершинної зв’язності G ;(G) 3 – число реберної зв’язності G ;

(G) 3 – мінімальна степінь вершин графа G . 9. Навести приклад графа G , для якого:

(G) 4 – число вершинної зв’язності G ;(G) 3 – число реберної зв’язності G ;

(G) 3 – мінімальна степінь вершин графа G .