
КДМ / Lektsii-DM
.pdf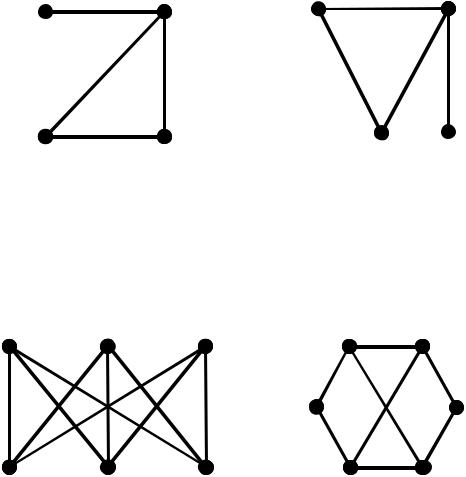
133
|
G (V,E) |
|
H {V ,E } |
|
V1 |
V2 |
V1 |
G5 |
V2 |
|
V4 |
V3 |
V4 |
V3 |
2) Довести ізоморфізм графів: G1 (V1 ,E1 ) G2 (V2 ,E2 ) .
|
G1 = (V1,E1) |
|
G2 = (V2,E2) |
|
1 |
2 |
3 |
6 |
1 |
5  2
2
4 |
5 |
6 |
4 |
3 |
Побудуємо бієкцію між множинами вершин цих двох графів: .
V1 V2
u V1 u |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
|
(u) V2 |
1 |
3 |
5 |
6 |
4 |
2 |
|
|
|
|
|
|
|
Доведемо, що бієкція зберігає відношення суміжності між вершинами графів. Це означає наступне: якщо деякі довільні вершини u, v є суміжними у графі G1 , то й відповідні їм за бієкцією вершини: (u), (v) також будуть суміжними у графі G2 .
Перевіримо цей факт для кожної із вершин графу G1 .
134
Вершина 1 графа G1 суміжна вершинам 4,5,6. Відповідна їй вершина 1
графа G2 |
повинна бути суміжна вершинам 6,4,2 |
графа G2 , що відповідають |
|||
вершинам 4,5,6 графа G1 : |
|
|
|
|
|
|
4 |
|
(4) |
6 |
|
|
|
|
|
|
4 . |
|
1 5 (1) |
1 (5) |
|||
|
|
|
|
|
2 |
|
6 |
|
(6) |
||
Вершина 2 графа G1 суміжна вершинам 4,5,6. Відповідна їй вершина 3 |
|||||
графа G2 |
повинна бути суміжна вершинам 6,4,2 |
графа G2 , що відповідають |
|||
вершинам 4,5,6 графа G1 : |
|
|
|
|
|
|
4 |
|
|
(4) |
6 |
|
|
(2) |
|
4 . |
|
|
2 5 |
3 (5) |
|||
|
|
|
|
|
2 |
|
6 |
|
|
(6) |
|
Вершина 3 графа G1 суміжна вершинам 4,5,6. Відповідна їй вершина 5 |
|||||
графа G2 |
повинна бути суміжна вершинам 6,4,2 |
графа G2 , що відповідають |
|||
вершинам 4,5,6 графа G1 : |
|
|
|
|
|
|
4 |
|
|
(4) |
6 |
|
|
(3) |
|
4 . |
|
|
3 5 |
5 (5) |
|||
|
|
|
|
|
2 |
|
6 |
|
|
(6) |
|
Вершина 4 графа G1 суміжна вершинам 1,2,3 . Відповідна їй вершина 6 |
|||||
графа G2 |
повинна бути суміжна вершинам 1,3,5 |
графа G2 , що відповідають |
|||
вершинам 1,2,3 графа G1 : |
|
|
|
|
|
|
1 |
|
|
(1) 1 |
|
|
|
|
(4) |
|
|
|
4 2 |
6 (2) 3 . |
|||
|
|
|
|
|
|
|
3 |
|
|
(3) 5 |
|
Вершина 5 графа G1 суміжна вершинам 1,2,3 . Відповідна їй вершина 4 |
|||||
графа G2 |
повинна бути суміжна вершинам 1,3,5 |
графа G2 , що відповідають |
|||
вершинам 1,2,3 графа G1 : |
|
|
|
|
|

|
|
|
135 |
1 |
|
(1) |
1 |
|
|
|
3. |
5 2 |
(5) 4 (2) |
||
|
|
|
5 |
3 |
|
(3) |
Хоча для вершини 6 графу G1 усі перевірки вже виповнені, повторимо той же хід розміркувань. Вершина 6 графа G1 суміжна вершинам 1,2,3 . Відповідна їй вершина 2 графа G2 повинна бути суміжна вершинам 1,3,5 графа G2 , що відповідають вершинам 1,2,3 графа G1 :
1 |
|
(1) |
1 |
|
|
|
3 . |
6 2 |
(6) 2 (2) |
||
|
|
|
5 |
3 |
|
(3) |
Необхідні умови ізоморфізму двох графів:
1)однакова кількість вершин;
2)однакова кількість ребер;
3)однакові ступеневі послідовності.
Наприклад.
1)Приклади графів, для яких виконуються необхідні умови ізоморфізму,
але графи не є ізоморфними. а)
б)
136
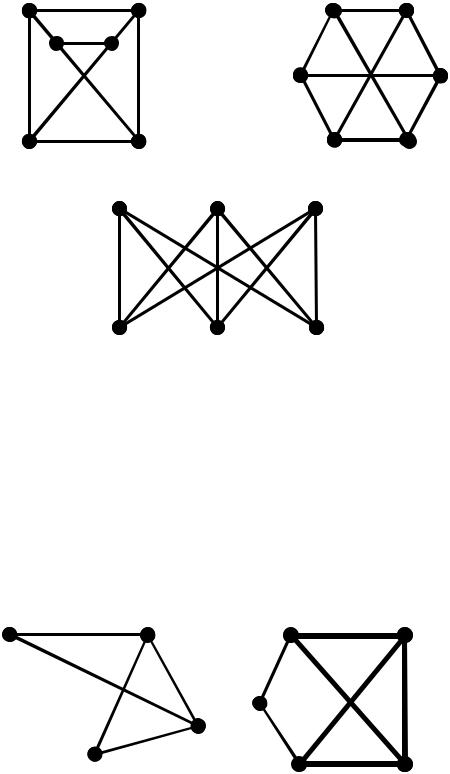
2) Графи, що зображено на рисунку нижче є ізоморфними між собою, більш того це два зображення відомого повного дводольного графу K3,3 (із задачі про три будинки та три колодязі).
5.7 Ізоморфна вкладеність
Граф H називається ізоморфно-вкладеним у граф G , якщо граф H є ізоморфним деякому породженому підграфу графа G .
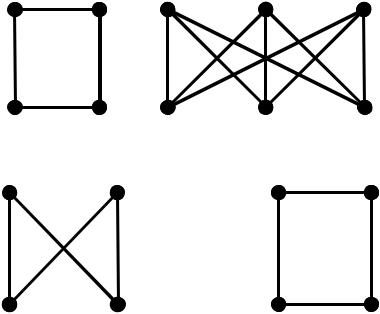
1) Граф H є ізоморфно-вкладеним у граф G за визначенням. Породжений підграф графу G , що ізоморфний графу H , виділений на
рисунку графу G .
H G
137 2) Граф H є ізоморфно-вкладеним у граф G , тому що він ізоморфний графу K2,2 , який у свою чергу є породженим підграфом графу G , що є графом
K3,3 .
H G
K2,2
5.8 Незалежна множина вершин графа
Незалежною множиною вершин (НМВ) графа G або внутрішньо-
стійкою множиною називається така підмножина S вершин графа G , що будьякі дві вершини цієї множини не суміжні між собою.
Підграф, породжений незалежною множиною, є порожнім.
Незалежна множина вершин називається максимальною, якщо вона не є власною підмножиною іншої незалежної множини із більшою кількістю вершин.
Незалежна множина вершин називається найбільшою, якщо вона найбільша за потужністю.
Потужність найбільшої незалежної множини називається числом незалежності.
Позначається число незалежності, як: (G) .
Наприклад.

138
1 |
2 |
3 |
4
8 |
6 |
|
|
|||
|
|
|
|
|
7 |
5 |
|
|
|
|
|
|
|
Si ,i |
|
|
– приклади незалежних множин. |
|||
1,10 |
||||||
S1 {1,3}, |
S2 {1,3,7}, |
S3 {1,4}, S4 {1,5,7}, S5 {2,4,8}, S6 {2,5,7,8}, |
||||
|
|
|
|
|
|
|
S7 {2,7,8}, S8 |
{3,6}, S9 {3,7,8},S10 {4,6}. |
|
|
|
|
||
Максимальними незалежними множинами є усі перераховані НМВ, окрім |
|||
підкреслених, |
тобто S 2 ,S 3 ,S4 ,S5 ,S6 ,S8 ,S9 ,S10 . Найбільша НМВ |
для |
|
зображеного графу – S6 , тому число незалежності дорівнює (G) 4. |
|
||
5.9 Кліка |
|
|
|
Клікою графа G називається така підмножина вершин S графа G , |
що |
||
будь-які дві вершини у ній суміжні. |
|
||
Кліка – антипод незалежної множини вершин. |
|
||
Підграф, породжений клікою, повним.
Максимальною клікою графа G називають таку кліку графа G , що не є власною підмножиною іншої кліки графа із більшим числом вершин.
Найбільша кліка – кліка максимальна за потужністю.
Потужність найбільшої кліки називається кліковим числом або
щільністю графа. Позначається: (G).
Наприклад.
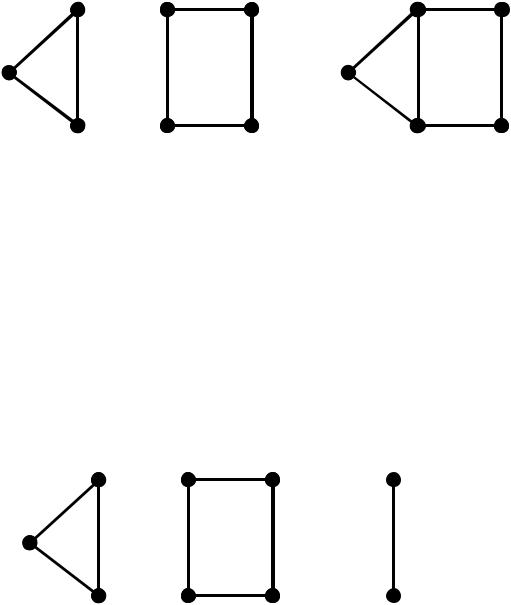
У наступному графі Si ,i 1,6 – кліки: S1 {1,2}, S2 {1,2,3}, S3 {2,3,4}, S4 {2,3,5}, S5 {2,4,5}, S5 {3,4,5}, S6 {2,3,4,5}. Серед них максимальними являються кліки: S2 {1,2,3},S6 {2,3,4,5}, а найбільшою – S6 {2,3,4,5},тому клікове число або щільність графу дорівнює: (G) 4 .
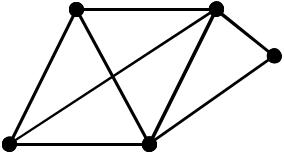
139
4 |
2 |
1
5 3
5.10 Домінуючі множини вершин графа
Домінуючою (зовнішньо-стійкою) множиною вершин (ДМВ) графа G
називається така підмножина вершин графа G , що
S V : v V \ S, w S, e {v,w} E ,
тобто для кожної вершини, що не входить у S , існує ребро, що йде в цю вершину із деякої вершини S .
Домінуюча множина називається мінімальною, якщо немає іншої домінуючої множини, що міститься в цій множині.
ДМВ являється найменшою, якщо вона має найменшу потужність серед всіх мінімальних ДМВ.
Потужність найменшої домінуючої множини називається числом домінування. Позначається (G) .
Зауваження
Незалежна множина вершин графа є максимальною (не обов’язково найбільшою), тоді й тільки тоді, якщо вона домінуюча.
Домінуюча множина вершин графа не обов’язково є незалежною множиною.
Підмножина вершин графа, що є одночасно незалежною та домінуючою називається ядром.
Наприклад.
Нехай задано граф G .
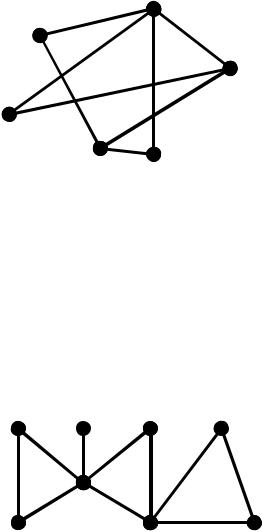
140
1
6
|
|
|
|
|
|
|
2 |
|
|
|
|
5 |
|
|
4 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Серед них |
тільки S1 |
{1,4,6} не є |
|
мінімальною ДМВ. |
Si ,i |
|
є |
|||
|
2,5 |
|||||||||
|
|
|
|
|
|
|||||
прикладами найменших ДМВ, |
тому число домінування для графу G дорівнює |
|||||||||
(G) 2 . ДМВ |
S6 {3,5,6} |
є |
мінімальною, |
але не найменшою. |
Домінуючі |
|||||
множини із другої по шосту є також незалежними множинами, а тому й ядрами цього графу.
2) Нехай задано граф H : |
|
|
|
1 |
2 |
3 |
7 |
|
4 |
|
5 |
6 |
8 |
Для графу H множини вершин {1,2,3,7} , {1,2,3,8}, {2,3,5,7} , {2,3,5,8}
являються прикладами найбільших незалежних множин вершин графу H , тому число незалежності для нього дорівнює (H) 4 .
А, наприклад, множина вершин {4,7} є максимальною, але не найбільшою
незалежною |
множиною. |
Усі |
множини |
вершин |
графу |
H : {1,2,3,7},{1,2,3,8},{2,3,5,7},{2,3,5,8} |
та {4,7} є також домінуючими, а тому й |
||||
ядрами цього графу. Але, наприклад, множина {4,6} є домінуючою, але не є незалежною.
З другої сторони, множина {4,6} являється мінімальною й найменшою ДМВ графу H , тому число домінування цього графу складає: (H) 2.
141
5.11 Операції над графами та їх елементами
5.11.1 Бінарні операції над графами
Нехай задано два неорієнтованих графа: G1 (V1 ,E1 ) та G2 (V2 ,E2 ) . Об'єднанням двох графів G1 та G2 називається такий граф G (V,E),
множина вершин якого є V V1 V2 та множина ребер є E E1 E2 . Ілюстрація операції об'єднання двох графів.
V2 |
V2 |
V5 |
V2 |
V5 |
V1 |
U |
= V1 |
V3 |
V3 |
V4 |
V3 |
V4 |
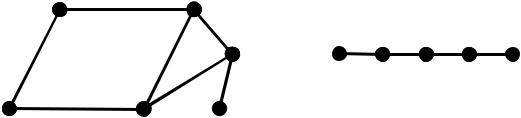
Перетином двох графів G1 і G2 називається такий граф G , у якого
множина вершин є V V1 |
V2 |
та множина ребер є E E1 E2 . |
|
|||
Непересічними графами |
називаються |
графи G1 |
і G2 |
такі, що |
||
E1 E2 та V1 V2 |
|
(немає загальних ребер та |
немає |
загальних |
||
вершин). |
|
|
|
|
|
|
Ілюстрація операції перетину двох графів. |
|
|
|
|||
V2 |
|
V2 |
V5 |
V2 |
|
|
V1 |
|
= |
|
|
V3 |
V3 |
V4 |
V3 |
142
5.11.2 Операції над елементами графів
До операцій над елементами графу відносять:
-операцію видалення вершини;
-операцію видалення ребра;
-операцію замикання або ототожнення вершин;
-операцію стягування ребер.
Видалення вершини
Нехай задано граф G (V,E) та його довільну вершину u V . Видалення вершини u – це унарна операція над графом G , що полягає у
побудові породженого підграфа графа G на множині вершин V \ {u} .
Видалення ребра
Нехай задано граф G (V,E) та його довільне ребро e E e, тоді граф G (V ,E ) G \ e виходить шляхом побудови підграфа графа G , із тією ж множиною вершин V V та множиною ребер E E \ {e}.
1) Ілюстрація операції видалення вершини v2 графу G .
При видаленні вершини, вочевидь, що видаляються ребра, для яких ця вершина є кінцевою.
G |
G\V2 |
V1 |
V2 |
|
V1 V3 V4 V5 V6 |
|
V5 |
V3 |
V4 |
V6 |
2) Ілюстрація операції видалення ребра e4 графу G .
