
КДМ / Lektsii-DM
.pdf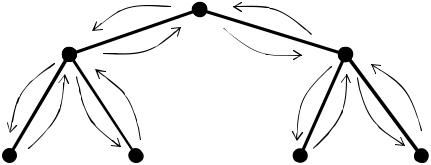
183
1. Спосіб обходу у глибину
Спосіб обходу у глибину складається з перегляду гілок дерева. Починаємо пошук з деякої фіксованої вершини v0 . Знаходимо вершину u суміжну з v0 і повторюємо весь процес, починаючи з вершини u . Якщо існує не переглянута вершина, суміжна з вершиною u , розглядаємо її й починаючи з неї продовжуємо пошук. Якщо не існує не однієї нової вершини, суміжної з u , то говорять, що вершина u використана й робиться повернення у вершину з якої потрапили у вершину u , продовжуємо процес. Якщо на якомусь кроці u v0 , і немає ні однієї використаної вершини, то алгоритм закінчує роботу.
Ілюстрація алгоритму обходу у глибину для графа, заданого матрицею суміжності, приведена на наступному рисунку, де у позначенні кожної вершини i : i / j указується номер її проходження при виконанні алгоритму, j.
Матриця суміжності: |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
c |
d |
e |
f |
g |
|
|
|
|
|
|
|
|
|
|
|
a |
|
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
b |
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
c |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
d |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
e |
|
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
f |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
g |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a /1 |
|
|
|
|
b / 2 |
|
|
|
|
|
|
e / 5 |
||
c / 3 |
d / 4 |
f / 6 |
g / 7 |

184
2. Спосіб обходу в ширину
Пошук в ширину означає перегляд вершин по ярусах в ієрархічному зображенні дерева. Під «використанням» вершини мається на увазі перегляд всіх «сусідів» (вершин, суміжних даній вершині) вершини.
a /1
b / 2 |
e / 3 |
c / 4 |
d / 5 |
f / 6 |
g / 7 |
7.7 Кістяки неорієнтованого графа
Кістяк (каркас, остов графа G ) – це остовний підграф графа G , що задає дерево на кожній компоненті зв'язності графа G .
Для зв'язного графа: кістяк – це дерево, що покриває всі вершини вхідного графа.
Очевидно, що в кожному графі існує кістяк, у загальному випадку не один. Ребра кістяка T деякого графа G називаються гілками, а ребра графа G , що не увійшли до кістяка називаються хордами.
Наприклад.
1) Нехай є деякий незв’язний неорієнтований граф G : v1 v2 v5
v6
v3 |
v4 |
v7 |

Приклади кістяків графа G :
а)
v1 v2
v3 v4
б)
v1 v2
v3 v4
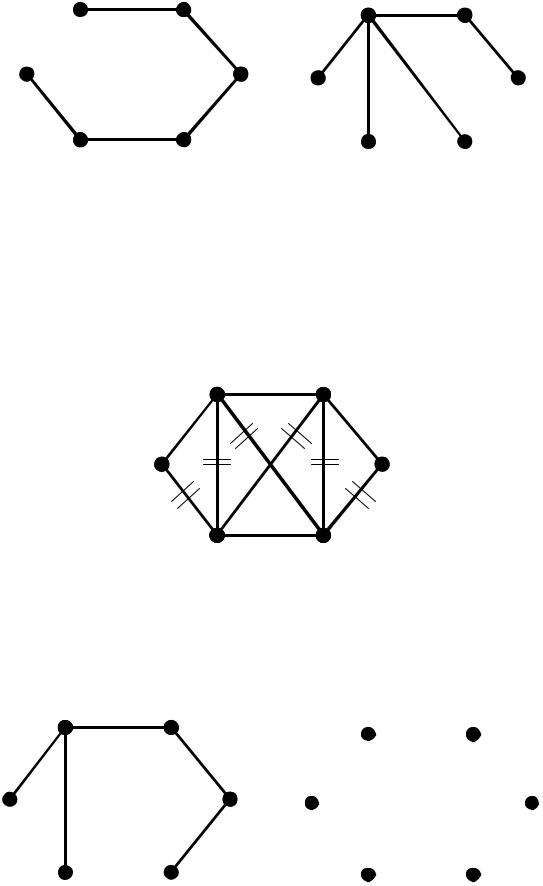
2)Нехай є деякий зв’язний граф G :
v2
v1
v6
185
v5
v6
v7
v5
v6
v7
v3
v4
v5
Приклади кістяків графа G :
186
v2 |
v3 |
v2 |
v3 |
v7 |
v4 v1 |
v4 |
v6 |
v5 |
v6 |
v5 |
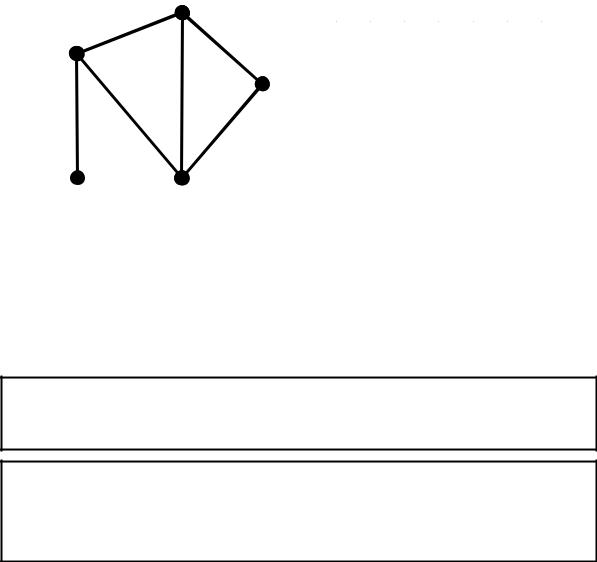
7.7.1 Алгоритми побудови кістяка
I клас. Видалення ребер вхідного графа.
Причому, чергове ребро, яке видаляється, не повинно робити граф не зв'язним, але повинно підтримувати ациклічність дерева.
II клас. Додавання ребра до порожнього графа.
Чергове ребро, яке додається, не повинне приводити до утворення циклу.
v2 |
v3 |
v2 |
v3 |
v1 |
v4 v7 |
v4 |
v6 |
v5 |
v6 |
v5 |
187
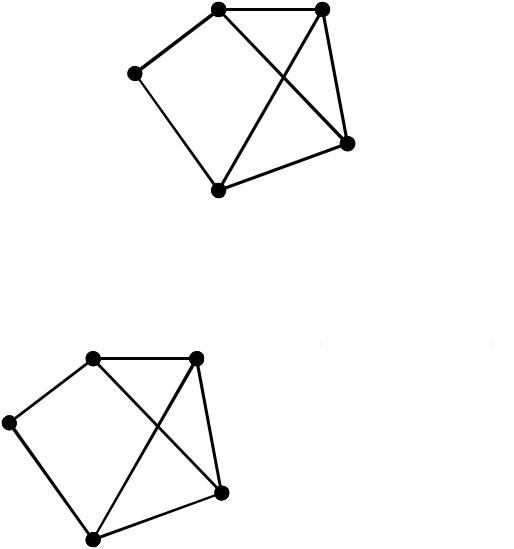
III клас. Кістяк найкоротших маршрутів (КНМ).
З довільної вершини алгоритм будує не просто дерево, а дерево на базі геодезичних.
7.7.2 Матриця Кирхгофа
Матриця Кирхгофа – це квадратна матриця:
M |
|
mij |
|
, |
i, j 1,...,p, |
deg vi , i j |
, |
|
|
|
|||||||
|
|
mij |
|
|||||
|
|
|
|
|
|
aij, |
i j |
|
|
|
|
|
|
|
|
||
де aij – відповідний елемент матриці суміжності
Наприклад.
Для графа G матриця Кирхгофа: v2
v1 |
|
v3 |
|
|
|
v1 |
v2 |
v3 |
v4 |
v5 |
|
|
|
|
v1 |
3 |
-1 |
0 |
-1 |
-1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
v2 |
-1 |
3 |
-1 |
-1 |
0 |
|
|
|
M= |
|
v3 |
0 |
-1 |
2 |
-1 |
0 |
v5 |
v4 |
|
|
|
v4 |
-1 |
-1 |
-1 |
3 |
0 |
|
|
|
v5 |
-1 |
0 |
0 |
0 |
1 |
||
|
|
|
|
|
Сума елементів будь-якого рядка й стовпця, як і сума усіх елементів матриці Кирхгофа, дорівнює 0.
7.7.3 Теореми Кирхгофа та Келі
Число кістякових дерев зв'язного графу G порядку p , p 2 дорівнює алгебраїчному доповненню будь-якого елемента матриці Кирхгофа
У зв'язному позначеному графі всі алгебраїчні доповнення матриці Кирхгофа рівні між собою й визначають загальне число позначених кістяків цього графа

188
Наслідок з теореми Кирхгофа
При p 1, де p – кількість вершин, число кістяків повного графа Kp дорівнює pp 2
Теорема Келі
Число позначених дерев порядку p дорівнює pp 2
Доведення.
Розглянемо матрицю Кирхгофа для повного графа Kp .
|
|
1 |
2 |
3 |
… |
p |
|
1 |
p-1 |
-1 |
-1 |
… |
-1 |
|
|
|
|
|
|
|
|
2 |
-1 |
p-1 |
-1 |
… |
-1 |
|
|
|
|
|
|
|
M= |
3 |
-1 |
-1 |
p-1 |
… |
-1 |
|
… |
… |
… |
… |
… |
… |
|
p |
-1 |
-1 |
-1 |
… |
p-1 |
|
|
|
|
|
|
|
Розглянемо алгебраїчне доповнення матриці Кирхгофа для елемента m11 . У новому визначнику буде p 1 рядків і p 1 стовпців.
|
|
1 |
2 |
3 |
… |
p-1 |
|
|
|
|
|
|
|
|
1 |
p-1 |
-1 |
-1 |
… |
-1 |
|
|
|
|
|
|
|
|
2 |
-1 |
p-1 |
-1 |
… |
-1 |
|
|
|
|
|
|
|
Am11: |
3 |
-1 |
-1 |
p-1 |
… |
-1 |
|
|
|
|
|
|
|
|
… |
… |
… |
… |
… |
… |
|
p-1 |
-1 |
-1 |
-1 |
… |
p-1 |
|
|
|
|
|
|
|
Виконаємо наступні еквівалентні перетворення:
1) додамо до першого рядка суму всіх інших рядків, перетворення типу:

189
(p 1) (p 2) ( 1) 1.
|
1 |
2 |
3 |
… |
p-1 |
1 |
1 |
1 |
1 |
… |
1 |
2 |
-1 |
p-1 -1 |
… -1 |
||
… … … … |
… … |
||||
p-1 -1 |
-1 -1 |
… p-1 |
|||
2) додамо перший рядок до інших;
|
1 |
2 |
3 |
… p-1 |
|
1 |
1 |
1 |
1 |
… |
1 |
2 |
0 |
p |
0 |
… |
0 |
… … … … |
… … |
||||
p-1 |
0 |
0 |
0 |
… |
p |
3) віднімаємо перший стовпець із інших.
|
1 |
2 |
3 |
… |
p-1 |
1 |
1 |
0 |
0 |
… |
0 |
2 |
0 |
p |
0 |
… |
0 |
… … … … |
… … |
||||
p-1 |
0 |
0 |
0 |
… |
p |
det Am11 pp 2 .
7.7.4 Алгоритми пошуку кістяків найкоротших маршрутів
Задано зважений граф G із матрицею ваги CG ,
G (V,E), CG 
 cij
cij 
 ,i, j 1,p,
,i, j 1,p,
де cij – вага ребра {i, j}, якщо воно існує.
Потрібно знайти кістяк з мінімальною сумарною вагою ребер.
190
7.7.4.1 Алгоритм Краскала
1.Впорядкуємо ребра вхідного графа в порядку неспадання їхньої ваги.
2.Будуємо порожній граф Op , де p кількість вершин вхідного графа.
3.На кожному кроці до вже сформованого графа зі списку ребер додається ребро з мінімальною вагою. Ребро, яке додається, не повинне приводити до утворення циклу.
4.Алгоритм закінчує роботу, якщо кількість ребер у сформованому графі стане рівним p 1.
Наприклад.
Знайти кістяк найкоротших маршрутів за алгоритмом Краскала.
v1 |
e1 |
v2 |
e2 |
e4 |
e6 |
v5 |
|
|
|
|
|
e3 |
e5 |
|
|
v3 |
|
|
|
e7 |
v4 |
|
|
Список ребер.
v1 |
1 |
v2 |
2 |
4 |
|
|
4 |
|
v5 |
|
|
|
|
|
|
5 |
|
3 |
|
v3 |
|
|
1 |
v4 |
|
|
(1, 2), (4, 3) |
1 |
(1, 5) |
2 |
(4, 5) |
3 |
(1, 3), (2, 3) |
4 |
(2, 4) |
5 |
191
Покрокове виконання алгоритму Краскала.
1.Побудувати порожній граф на 5 вершинах.
v1 v2
v5
 v3
v3
v4
2. Додати 2 перші ребра зі списку ребер: e1 і e7 . v1 1 v2
v5 
v3
1
v4
3. Додати ребро довжиною 2 e2 .
v1 1 v2
2
v5
v3
1
v4

192
4. Додати ребро довжиною 3 e3 .
v1 1 v2
2
v5
3
v3
1
v4
Результат застосування алгоритму Краскала Кістяк найкоротших маршрутів має довжину: 7.
v1 e1 v2 e2 
v5
e3 |
v3 |
|
e7
v4
7.7.4.2 Алгоритм Прима
Відрізняється від алгоритму Краскала тим, що на кожному кроці будується не просто граф без циклів, але дерево.
1.Впорядкуємо ребра вхідного графа в порядку не спадання їхньої ваги.
2.Будуємо порожній граф Op , де p кількість вершин вхідного графа.
3.На кожному кроці до формованого графа додаємо таке ребро зі списку ребер, щоб не утворився цикл і не порушувалася зв'язність.
