Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донецкий национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

метода по вышке 211

.pdf

Скачиваний:

Добавлен:

03.03.2016

Размер:

1.22 Mб

Скачать

☆

1 / 71 2 3 4 5 6 7 > Следующая >>>

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД

«ДОНЕЦЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ» АВТОМОБІЛЬНО-ДОРОЖНІЙ ІНСТИТУТ

«ЗАТВЕРДЖУЮ» Директор АДІ ДВНЗ «ДонНТУ»

М.М. Чальцев 26.05.2011 р.

Кафедра «Вища математика»

МЕТОДИЧНІ ВКАЗІВКИ ДЛЯ ПІДГОТОВКИ ДО МОДУЛЬНОГО КОНТРОЛЮ З

ДИСЦИПЛІНИ «ВИЩА МАТЕМАТИКА» (ВЕКТОРНА ТА ЛІНІЙНА АЛГЕБРА, АНАЛІТИЧНА ГЕОМЕТРІЯ, ГРАНИЦЯ ФУНКЦІЇ, ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ) ДЛЯ СТУДЕНТІВ УСІХ СПЕЦІАЛЬНОСТЕЙ

02/12-2011-03

«РЕКОМЕНДОВАНО»	«РЕКОМЕНДОВАНО»
Навчально-методична комісія	Кафедра «Вища математика»
Автомобільно-дорожнього	Протокол № 10 від 30.03.2011р.
інституту ДВНЗ ДонНТУ
Протокол № 4 від 18.04.2011р.

Горлівка – 2011

ДВНЗ«ДонНТУ» Автомобільно-дорожній інститут

УДК 517.2 +517.3+517.5 (071)

Методичні вказівки для підготовки до модульного контролю з дисципліни «Вища математика» (векторна та лінійна алгебра, аналітична геометрія, границя функції, диференціальне числення функції однієї змінної) (для студентів усіх спеціальностей) [Електронний ресурс] / укладачі: Л.П. Вовк, Є.О. Корольов, Т.В. Непомняща. – Електрон. дані – Горлівка: ДВНЗ «ДонНТУ» АДІ, 2011. – 1 електрон. опт. диск (CD-R); 12 см. –

Систем. вимоги: Pentium; 32 RAM; WINDOWS 98/2000/NT/XP; MS Word 2000. – Назва з титул. екрану.

Вказівки відповідають розділам векторна та лінійна алгебра, аналітична геометрія, границя функції, диференціальне числення функції однієї змінної дисципліни «Вища математика» для підготовки бакалаврів. Містять приклади розв’язання типових завдань із зазначених розділів, а також матеріали для самостійної підготовки студентів до модульної контрольної роботи. Методичні вказівки призначено для студентів перших курсів усіх спеціальностей.

Укладачі:	Вовк Л.П., д.т.н., проф.
	Корольов Є.О., к.ф.-м.н., доц.
	Непомняща Т.В.

Відповідальний за випуск:	Максимова Т.С., к.п.н., доц.
	каф. «Вища математика»

Рецензент:	Луценко Л.І., к.ф.-м.н., доц.
	каф. «Вища математика»

«Вища математика»

		3
	ЗМІСТ
ВСТУП .......................................................................................................		4
МОДУЛЬ 1 ................................................................................................		5
1.1	Приклади розв’язування типових задач..........................................	5
1.2	Завдання для самостійної підготовки студентів до модульного
контролю........................................................................................................		23
1.3	Теоретичні запитання до модуля 1................................................	29
МОДУЛЬ 2 ..............................................................................................		32
2.1	Приклади розв’язування типових задач........................................	32
2.2	Завдання для самостійної підготовки студентів до модульного
контролю........................................................................................................		47
2.3	Теоретичні запитання до модуля 2................................................	61
СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ ........ .................................		63

ДВНЗ«ДонНТУ» Автомобільно-дорожній інститут

ВСТУП

Вища математика є основою багатьох теоретичних і прикладних наук, тому володіння математичним апаратом необхідне студентам вищих технічних навчальних закладів для успішного вивчення багатьох дисциплін (теоретичної механіки, опору матеріалів і т.д.), для засвоєння спеціальних курсів і подальшої професійної діяльності.

Представлені до Вашої уваги методичні вказівки створено з метою допомогти студентам в усвідомленні та застосуванні теоретичних фактів з векторної та лінійної алгебри, аналітичної геометрії, теорії границь, диференціального числення функції однієї змінної в умовах модульнорейтингової системи навчання і оцінювання знань.

У даний навчальний посібник включено приклади розв’язання типових задач, а також матеріали для підготовки до модульної контрольної роботи: практичні завдання і теоретичні запитання, тому він може використовуватися студентами у самостійній роботі з вищої математики, підготовці до модульної контрольної роботи.

Бажаємо успіхів!

«Вища математика»

МОДУЛЬ 1

1.1 Приклади розв’язування типових задач

Задача №1. Дана система лінійних рівнянь:

2x		+ x	2	− x	3	=1,
	1		2	− 2x	3	=1,	(1.1)
3x		+ 2x		− 2x		=1,	(1.1)
x	1	− x	2	+ 2x3		= 5.
1			2	3

Довести її сумісність і розв'язати трьома способами:

1)методом Гаусса;

2)методом Крамера;

3)методом оберненої матриці.

Розв'язання. Для доведення сумісності системи лінійних рівнянь (1.1) використовуємо теорему Кронекера-Капеллі: для того щоб система лінійних рівнянь була сумісною, необхідно і достатньо, щоб ранг основної матриці системи А (матриця, складена з коефіцієнтів при невідомих) дорівнював рангу її розширеної матриці С (матриця, отримана з основної матриці системи додаванням стовпчика вільних членів). При цьому, якщо ранг матриці дорівнює числу невідомих, то система лінійних рівнянь має єдиний розв’язок, а якщо менше, то система має безліч розв’язків.

Складемо розширену матрицю системи лінійних рівнянь (1.1) і приведемо її до східчастого вигляду за допомогою елементарних

перетворень:
2 1			−1	1		1	−1 2		5		1	−1 2		5	1 −1 2				5

	3	2	− 2	1		3	2	− 2	1		0	5	−8	−14		0	5	−8	−14
					~					~					~					.
	1	−1 2		5		2	1	−1	1		0	3	−5	−9		0	0	−1	−3

Тут ми послідовно зробили наступні перетворення:

1.c1 ↔ c3 ;

2.c2 := c2 −3c1, c3 := c3 − 2c1 ;

3.c3 := 5c3 −3c2 .

Отже, східчаста матриця системи (1.1) має вигляд:
1		−1	2	5

	0	5	−8	−14		(1.2)
А =					.
	0	0	−1	−3

На підставі (1.2) можемо зробити висновок, що ранг матриці системи (1.1) дорівнює 3 (вона має три ненульових рядка), ранг її розширеної

= ~ =

матриці також дорівнює 3 ( r (A) r (А) 3 ). За теоремою КронекераКапеллі система рівнянь (1.1) є сумісною і має єдиний розв’язок.

ДВНЗ«ДонНТУ» Автомобільно-дорожній інститут

Розв`яжемо систему лінійних рівняння за допомогою метода Гаусса. Від матриці (1.2) перейдемо до системи:

x1 − x2 + 2 x3 = 5,
	5x2 −8 x3 = −14,	(1.3)
	− x3 = −3,
	− x3 = −3,

яка рівносильна системі (1.1).

Із системи (1.3) послідовно знаходимо:

x1 =1; x 2 = 2; x 3 = 3.

Для перевірки підставимо отримані значення невідомих в (1.1):

2	1 + 2 − 3 =1,
	1 + 2 2 −2 3 =1,
3	1 + 2 2 −2 3 =1,
	− 2 + 2 3 = 5.
1	− 2 + 2 3 = 5.

Отримали вірні рівності. Отже, отримані значення невідомих задовольняють системі (1.1).

2) Знайдемо розв’язок системи (1.1) за формулами Крамера. Визначники обчислимо за правилом трикутників.


	2			1		−1

=	3 2 − 2							= 2 2 2 +1 (−2) 1 +3 (−1) (−1) −(−1) 2 1 −1 3 2 −
	1			−1		2
−(−2) (−1) 2 =1,
		1		1		−1

1 =		1 2 − 2							=1 2 2 +1 (−2) 5 +1 (−1) (−1) −(−1) 2 5 −1 1 2 −
		5		−1		2
−(−2) (−1) 1 =1,
			2	1		−1

2 =			3 1		− 2		= 2 1 2 +1 (−2) 1 +3 5 (−1) −(−1) 1 1 −1 3 2 −
			1	5		2
−(−2) 5 2 = 2,
2				1		1
3 = 3 2 1 = 2 2 5 +1 1 1 +3 (−1) 1 −1 2 1 −1 3 5 −

1−1 5

−1 (−1) 2 = 3.

x =	1 ; x	2	=	2 ; x	=	3 x	=1; x	2	= 2; x	= 3.
1		2		3		1		2	3

«Вища математика»

3) Знайдемо розв'язок системи (1.1) засобами матричного числення за формулою

X = A−1B ,

(1.4)

де

2 1 −1

3 2

− 2

A =

; X = x

; B =

1 −1 2

Обернену матрицю А−1 до

основної

матриці А

знайдемо за

формулою:

A−1

A12

A22

A32

(1.5)

де

– визначник (детермінант) матриці А;

Аij (i =1,2,3; j =1,2,3)

–

алгебраїчні

доповнення

елементів

матриці A .

−1

− 2

=1.

−1

Алгебраїчні доповнення Аij

обчислимо за формулою

Aij

= (−1)i+ j

M ij ,

(1.6)

де Mij

– мінори елементів aij

матриці A .

Використовуючи формулу (1.6), знаходимо:

1+1

− 2

= 2;

A11 = (−1)

−1

1+2

− 2

= −8;

A12 = (−1)

1+3

= −5;

A13 = (−1)

−1

A21 = (−1)

2+1

−1

= −1;

−1

ДВНЗ«ДонНТУ» Автомобільно-дорожній інститут

A22		= (−1)				2+2					2		−1			= 5;
						2+2					2		−1
											1	2
											1	2
A23		= (−1)				2+3				2		1				= 3;
						2+3				2		1
										1			−		1
										1			−		1
A31		= (−1)			3+1			1					−1			= 0;
					3+1			1					−1
								2				−		2
								2				−		2
A32		= (−1)			3+2					2			−1			=1;
					3+2					2			−1
										3			−		2
										3			−		2
A33		= (−1)			2+3				2			1			=1.
					2+3				2			1
									3			2
									3			2
Підставимо отримані значення							для						A			й Аij у формулу (1.5),
Підставимо отримані значення							для						A			й Аij у формулу (1.5),
одержимо:				2			−1					0
			1	2			−1					0
	−1	=	1	−8
A							5					1			.
A			1				5					1			.
			1	−5			3					1
				−5			3					1

Із формули (1.4) отримаємо:
x1			2	−1 0	1		2 1−1 1+0 5		1
			−8	5 1	1		−8 1+5 1+1 5		2
x	2	=	−8	5 1	1	=	−8 1+5 1+1 5	=	2	.
	2		−5	3 1			−5 1+3 1+1 5
x 3			−5	3 1	5		−5 1+3 1+1 5		3

З отриманого матричного рівняння випливає: x1 =1; x 2 = 2; x 3 = 3.

Відповідь: Задана система лінійних рівнянь сумісна і має єдиний розв'язок: x1 =1; x 2 = 2; x 3 = 3.

Задача №2. Дані координати вершин піраміди A1A2 A3 A4 : A1(2;−1;1);

A2 (5;5;4); A3(3;2;−1); A4 (4;1;2). Знайти:

1)довжину ребра A1A2 ;

2)кут між ребрами A1A2 і A1A4 ;

3)кут між ребром A1A4 і гранню A1A2 A3;

4)площу грані A1A2 A3;

5)об'єм піраміди;

6)рівняння прямої A1A2 ;

7)рівняння площини A1A2 A3;

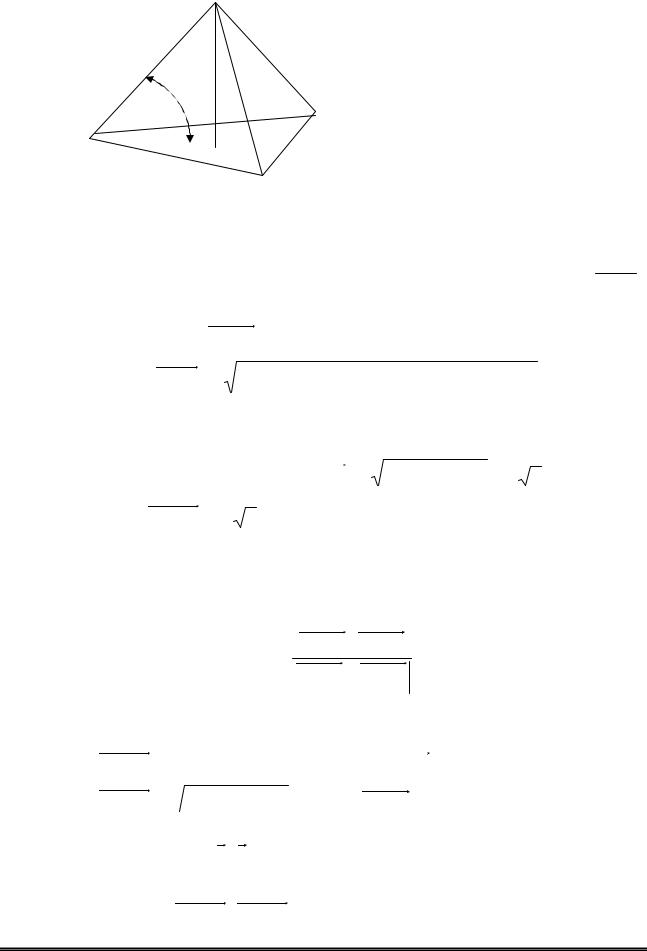
8) рівняння висоти, опущеної з вершини A4 на грань A1A2 A3. Зробити схематичне креслення (рис. 1.1).

«Вища математика»

А4

ϕ А2

А1 А5

А3 Рисунок 1.1 – Піраміда

1) Визначимо довжину ребра A1A2 .

Розв'язання. Довжина ребра A1A2 дорівнює довжині вектора A1A2 , координати й довжину якого визначимо за формулами:

A1A2 ={x2 − x1; y2 − y1; z2 − z1},

(1.7)

A A

− x

)2 + (y

− y )2 + (z

− z )2

(1.8)

1 .

Підставивши у формули (1.7), (1.8) координати

точок A1

і A2 ,

одержимо:

A1A 2 ={3;6;3},

A1A 2

32 +62 +32 = 3 6.

Відповідь:

A1A 2

= 3

6 (лін.од).

2) Визначимо кут між ребрами A1A2 і A1A4 .

Розв'язання. Кут між ребрами дорівнює куту між векторами

A1A2

. Кут ц між векторами визначимо за формулою

A1A4

cos ϕ =

(A1A2

A1A4 ).

(1.9)

A1A2

A1A4

Координати і довжину вектора

обчислимо за формулами (1.7),

A1A4

(1.8).

A1A 4 ={4 −2;1+1; 2 −1}, звідки A1A 4 ={2; 2;1},

A1A 4 = 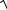22 +22 +12 , звідки A1A4 = 3 (лін.од). Скалярний добуток визначається формулою:

(a b)= axbx + ayby + azbz .

(1.10)

Використовуючи формулу (1.10), отримаємо:

(A1A 2 A1A 4 )= 3 2 +6 2 +3 1 = 21.

ДВНЗ«ДонНТУ» Автомобільно-дорожній інститут

10
Підставивши отримані		значення для				у		,		, (			)

							A1A2		A1A4		A1A2	A1A4
формулу (1.9), одержимо:
cos ϕ =	21	=	7		= 0,9525,	звідки ц ≈ 17, 71˚.
cos ϕ =	3 6	=	3	6	= 0,9525,	звідки ц ≈ 17, 71˚.
3	3 6		3	6

Відповідь: Кут між ребрами A1A2 і A1A4 ц ≈ 17, 71˚. 3) Визначимо кут між ребром A1A4 і гранню A1A2 A3.

Розв'язання. Кут б між ребром A1A4 і гранню

A1A2 A3 знайдемо за

формулою:

N ) ,

sin α =

(1.11)

де A - напрямний вектор прямої А1А2; N –

нормальний вектор

площини A1A2 A3.

Візьмемо вектор

у якості напрямного вектора A прямої A1A4 , а

A1A4

вектор нормалі N площини A1A2 A3 знайдемо за формулою

N = A1A3 × A1A2 .

Координати вектора A1A3 визначимо за формулою (1.7):

A1A3 ={3−2;2 +1;-1-1},

звідки A1A3 ={1;3;−2}.

Векторний добуток обчислюється за формулою:

(1.12)

Застосовуємо формулу (1.12):

(3 3 −(−2) 6)−

(1 3 −(−2) 3)+

(1 6 −3 3)=

N = A1A3 × A1A2 =

1 3 − 2

= 21i −9 j −3k.

Довжину			вектора N = A1A3 × A1A2 ={21;−9;−3} визначимо за
формулою (1.8):
	N	=	(21)2 +(−9)2 +(−3)2 , звідки	N	= 531 (лін.од.).

Скалярний добуток (l N ) обчислимо за формулою (1.10): (A N) = 2 21 + 2 (−9) +1 (−3), звідки (l N ) =21.

«Вища математика»

1 / 71 2 3 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
03.03.2016645.4 Кб3Метод_ИР - Основы механики ХимОборуд_А4.pdf
#
03.03.20161.6 Mб28Метод_курс_ТЭС2.doc
#
15.11.2019419.84 Кб1Метода ОПУТ4-2.doc
#
03.03.20162.55 Mб87метода 2013.doc
#
03.03.2016478.72 Кб6Метода Інд Економіка і бізнес.doc
#
03.03.20161.22 Mб5метода по вышке 211.pdf
#
03.03.20162.81 Mб58Метода ТИС_03.12.11.doc
#
17.11.2018379.39 Кб2Методические рекомендации (1).doc
#
03.03.2016434.69 Кб64Методические указания (право).doc
#
03.03.20161 Mб17Методические указания и контрольные задания по промышленной электронике .doc
#
03.03.2016253.44 Кб4Методические указания курс.doc