
метода по вышке 211
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
41 |
|
|
|
|
|
|
|
|
|
y′′2 |
= |
d 2 y |
= |
|
|
dy′x |
= |
|
( y′x )′t |
. |
|
|
|
(2.5) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
dx 2 |
|
|
|
|
|
dx |
|
|
|
|
xt′ |
|
|
|
|
|
|
|
||||||
Знаходимо похідні від х і від у за параметром t: |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
= x' |
= 2t + 2; |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
= y' |
= |
|
|
1 |
|
. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
t |
+1 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Шукану похідну від у по х знаходимо за формулою (2.4): |
|
||||||||||||||||||||||||||||||||||||
y′x = |
dy |
= |
|
y′t |
|
= |
|
|
1 |
|
|
|
|
|
|
|
= |
|
|
1 |
= |
1 |
(t +1) |
−2 |
. |
||||||||||||
dx |
|
|
|
|
|
(t +1)(2t +2) |
2(t +1)2 |
2 |
|
||||||||||||||||||||||||||||
|
|
|
x′t |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Далі знаходимо похідну від |
|
|
y′x |
за параметром t, а потім шукану |
|||||||||||||||||||||||||||||||||
другу похідну за формулою (2.5): |
|
|
dy′x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(y′x )′t = |
|
|
= −(t +1) −3 ; |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−(t +1)−3 |
|
|
|
|||||||||
|
|
|
|
|
|
|
y′′ |
2 = |
dy′x |
|
= |
(y′x )′t |
= |
. |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
dx |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
x |
|
|
|
|
|
|
x′t |
1 |
|
|
|
|
2(t +1) |
|
|
|
|
|||||||||||||
Відповідь: y′x = |
(t + |
1) −2 ; y′′2 |
|
= − |
(t +1) −4 . |
|
|
|
|
|
|||||||||||||||||||||||||||
2 |
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Переходимо |
до |
|
|
розв'язання |
|
|
задач |
|
про найбільші |
або найменші |
|||||||||||||||||||||||||||
значення величин. Для розв'язання таких задач потрібно, виходячи з умови, вибрати незалежну змінну й виразити досліджувану величину через цю змінну, а потім знайти шукане найбільше або найменше значення отриманої функції. При цьому інтервал зміни незалежної змінної, який може бути кінцевим або нескінченним, також визначається з умови задачі.
Задача №17. Машина доставляє зерно на елеватор по степовій дорозі, а потім по шосе. Під яким кутом до шосе повинна проходити степова дорога, щоб машини витрачали найменший час на весь шлях, якщо по степовій дорозі швидкість машини у k разів менша, ніж по шосе?
Розв'язання. Зробимо рисунок до задачі:
D |
С |
B |
α
A
Рисунок 2.1 – Схема місцевості
ДВНЗ«ДонНТУ» Автомобільно-дорожній інститут
42
Нехай машина доставляє зерно з пункту А в пункт В. Відрізок АС зображує степову дорогу, а відрізок СВ – шосе (рис. 2.1). Час, витрачений на перевезення зерна, складається із часу проїзду по дорогах АС і СВ. Позначимо швидкість руху по дорозі АС через v, тоді, згідно з умовою, швидкість руху по шосе дорівнює k·v.
Позначимо кут, під яким степова дорога проходить до шосе, б; величину відрізка AD DB через A, а величину відрізка DB через а.
Розглянемо ∆ADC:
|
AC = |
A |
|
, CB = a - Actg б. |
|
|
|
||||||
|
sin б |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Час руху машини розглянемо як функцію кута б: |
|
||||||||||||
t(α) = |
A |
+ |
a −Actg б |
= |
A |
+ |
a |
− |
A |
ctg б. |
|||
v sin б |
|
vsin б |
kv |
kv |
|||||||||
|
|
|
kv |
|
|
|
|
|
|||||
Визначимо критичну точку. Для цього обчислимо першу похідну:
′ |
A |
|
cos б |
|
|
1 1 |
|
||
t (α) = |
|
|
− |
|
+ 0 |
+ |
|
|
; |
|
|
|
|
||||||
|
|
|
|
sin 2б |
|
|
|
|
|
|
v |
|
|
|
k sin 2б |
||||
′ |
|
cos б |
1 |
|
|
1 |
|
|||
t (α) = 0; - |
|
|
+ 0 + |
|
|
|
|
= 0; |
||
sin 2б |
k |
sin 2б |
||||||||
|
k cos α =1; |
cos α = |
1 |
. |
|
|||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
k |
|
|
Для дослідження критичної точки обчислимо другу похідну:
|
|
|
|
|
|
|
|
|
sin |
3 |
б − |
2 sin б cos |
2 |
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
′′ |
|
|
A |
|
|
|
|
|
|
|
|
|
|
2 sin б cos б |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
4 |
|
|
= |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
t (α) = |
|
|
|
|
|
|
|
|
|
|
|
|
sin |
б |
|
|
|
|
|
|
|
|
|
k sin |
б |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ k cos |
2 |
б |
|
|
|
|
|
|
|
= |
|||||||||
A sin б(1 + cos |
|
|
б) − 2 cos б = |
|
A k |
|
|
|
− 2 cos б |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
sin |
4 |
б |
|
|
|
|
|
|
|
|
|
|
|
k sin |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k sin |
3 |
б |
|
|
|
||||||||||||||||
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
A k + k cos2б − 2 cos б |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kv |
|
|
|
|
|
|
|
|
sin3б |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Обчислимо значення другої похідної при cos б = |
|
: |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
k |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
sin б = |
|
1 − cos2б = |
|
|
1 − |
1 |
|
|
|
= |
k 2 −1 |
; |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k 2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
k + k |
|
|
|
|
|
|
|
− 2 |
|
|
|
|
|
|
|
|
|
|
k3 k |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
A |
|
|
|
k |
2 |
|
|
k |
|
|
A |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
Ak |
|
||||||||||||||||||||||||
|
|
t′′ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
> 0. |
||||||||||||||||||
|
|
kv |
|
|
|
k |
2 |
|
|
|
|
|
3 |
|
kv |
|
(k2 −1) k2 −1 |
v k 2 −1 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
«Вища математика»

43
З рис. 2.1 видно, що cos б = k1 ≤ ABa .
На вказаному проміжку функція t(б) має єдиний екстремум-мінімум. Отже, з ним збігається найменше значення функції.
Відповідь. Якщо швидкість по шосе в k раз більша за швидкість по степовій дорозі, то степова дорога має проходити до шосе під кутом, що
визначається співвідношенням cos б = k1 .
Задача №18. Дослідити функцію методами диференціального числення та побудувати її графік, використовуючи дані дослідження.
y = x 3 −6x 2 +25x −28 .
2(x −2) 2
Розв'язання.
Дослідження функції проведемо за планом:
1)Знайти область існування функції.
2)Знайти (якщо це можливо) точки перетину графіка з осями координат.
3)Дослідити функцію на періодичність, парність і непарність.
4)Знайти точки розриву, дослідити їх.
5)Визначити інтервали монотонності, точки локальних максимумів і мінімумів графіка функції.
6)Встановити області опуклості та вгнутості, а також точки перегину графіка функції.
7)Знайти асимптоти кривої.
8)Побудувати графік функції, враховуючи проведені дослідження. Реалізація плану
1.Функція існує для всіх значень х, за винятком х=2.
2.Знаходимо точку перетину з віссю Оу. Для цього покладемо в рівнянні x=0, тоді y=-3,5. Отже, графік даної функції перетинає вісь Оy у
точці (0;-3,5).
Знаходимо точку перетинання з віссю Ох. Покладемо y=0, тоді одержимо рівняння:
x3 −6x2 + 25x − 28 = 0 .
Оскільки даний многочлен є зведеним і має цілі коефіцієнти, то, якщо він має раціональні корені, вони є цілими і знаходяться серед дільників вільного члена. Підставимо у рівняння x = ±1;±2;±4;±7;±14;±28 . Жодне з цих значень не є коренем, тому дане рівняння не має раціональних коренів.
3. Функція не періодична, загального типу, тобто її графік не є симетричним по відношенню до координатних осей.
ДВНЗ«ДонНТУ» Автомобільно-дорожній інститут

44
4. Функція в точці х=2 має розрив другого роду:
lim |
x3 |
−6 x2 + 25x −28 |
= ∞. |
|
2(x −2) 2 |
||
x→2±0 |
|
|
5. Знаходимо першу похідну, дорівнюємо її до нуля і нескінченності. Одержуємо:
y′ = (3x2 −12x + 25)2(x − 2)2 − 4(x − 2)(x3 −6x2 + 25x − 28) = 4(x − 2)4
= x3 −6x2 − x + 6 .
Звідки:
x 3 −6x 2 −x +6 = 0.
Корені цього рівняння: -1; 1; 6. Прирівнюючи до нескінченності, знаходимо:
x 3 −6x 2 −x +6 = ∞, 2(x −2)3
звідки x-2=0, тобто x=2.
Для дослідження на максимум і мінімум у стаціонарних точках (коріння рівняння y′ = 0) знаходимо другу похідну даної функції:
|
|
|
|
|
8 |
||
|
|
|
13 x − |
|
|
||
|
|
|
|
||||
|
′′ |
= |
|
|
13 |
|
|
y |
|
(x −2) 4 . |
|||||
|
|
||||||
Визначаємо знак другої похідної в отриманих стаціонарних точках: y′′(−1) < 0; y′′(1) > 0; y′′(6) > 0.
Отже, при x1 = −1 функція досягає максимуму, при x 2 =1 і x 3 = 6 –
мінімуму. Значення функції x при цих значеннях х: y(−1) = −3,3; y(1) = -4; y(6) = 3,8 .
Знаючи точки екстремуму, легко встановити області зростання й спадання функції:
для-∞ <x<-1 функція зростає; для-1<x<1 функція спадає; для1<x<2 функція зростає; для2<x<6 функція спадає; для6<x<∞ функція зростає.
«Вища математика»

45
6. Встановлення областей опуклості і вгнутості, а також точок перегину. Для знаходження точок перегину дорівнюємо другу похідну до
нуля. Одержуємо y′′ = 0, тобто x −138 = 0 , звідки x = 138 .
При переході через значення x = 138 друга похідна змінює знак:
|
8 |
|
|
|
8 |
|
|
|
|||
y′′ |
|
|
|
−h |
< 0; y′′ |
|
|
|
+h |
> 0. |
|
13 |
13 |
||||||||||
|
|
|
|
|
|||||||
Щоб встановити області опуклості й вгнутості, розглянемо знак другої похідної у наступних проміжках:
|
|
|
|
|
|
(−∞, |
|
8 |
) , ( |
|
8 |
,2) , (2,+∞) . |
|
||
|
|
|
|
|
|
|
|
|
|||||||
Маємо: |
|
|
|
13 |
|
13 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
8 |
|
|
y′′< 0 |
|
|
|
|
|
|
|
|
|
|||
для − ∞ < x < |
|
, |
|
|
- крива опукла; |
|
|||||||||
13 |
|
|
|
||||||||||||
|
8 |
|
|
|
′′ |
|
|
|
|
|
|
|
|
|
|
для 13 < x < 2, y |
> 0 - крива вгнута; |
|
|||||||||||||
|
|
||||||||||||||
для 2 < x < +∞, |
y′′ > 0 |
|
|
- крива вгнута. |
|
||||||||||
7. Рівняння похилої асимптоти будемо шукати у вигляді: |
|
||||||||||||||
де |
|
|
y=kx+b, |
|
|
|
|
(2.6) |
|||||||
|
|
|
|
|
|
|
f (x) |
|
|
||||||
|
|
|
|
|
|
k = lim |
|
, |
(2.7) |
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
x→∞ |
|
x |
|
||||||
|
|
|
|
|
|
b = lim [f (x) −kx]. |
(2.8) |
||||||||
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
||||
За формулами (2.7) і (2.8) знаходимо k і b:
|
k = |
lim |
|
x3 |
|
−6x 2 + 25x −28 |
= |
|
1 |
; |
|
||||
|
|
|
|
|
2x(x −2)2 |
2 |
|
||||||||
|
|
x →∞ |
|
|
|
|
|
|
|
||||||
|
|
x3 |
−6x2 + 25x − 28 |
|
1 |
|
|
= −1. |
|||||||
|
b = |
lim |
|
|
|
|
|
|
|
− |
|
|
x |
||
|
|
|
|
|
|
2x(x − 2)2 |
2 |
||||||||
|
x→∞ |
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
Згідно з (2.6) маємо y = |
x |
−1. |
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
Знайдемо вертикальні асимптоти. Для цього розв`язуємо рівняння |
||||||||||||||
= 0 , тобтоx −2 = 0 , звідки x=2. |
|
|
|
|
|
|
|||||||||
y |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тому графік буде необмежено наближатися до вертикальної асимптоти у верхній її частині, оскільки lim y = +∞.
x→2±0
ДВНЗ«ДонНТУ» Автомобільно-дорожній інститут
46
Тепер установимо взаємне розташування кривої й асимптоти y = 12 x −1.
Для цього складемо різницю ординат кривої і асимптоти:
|
x 3 −6x 2 + |
25x −28 |
− |
1 |
x |
+1 = |
13x −20 |
. |
|
|
|||||||
|
2(x −2)2 |
|
|
|
2 |
2(x −2)2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ця різниця дорівнює |
нулеві |
|
при |
x = |
|
20 |
, тобто графік кривої |
||||||||||
|
13 |
||||||||||||||||
|
|
20 |
|
3 |
|
|
|
|
|
|
20 |
||||||
|
|
|
|
|
|
|
|
|
|||||||||
перетинає асимптоту в точці |
|
|
, - |
|
|
|
|
. На проміжку − ∞, |
|
ця різниця |
|||||||
|
13 |
|
|||||||||||||||
|
|
13 |
|
|
|
|
|
|
|
|
|
13 |
|||||
від`ємна, отже, графік кривої знаходиться під асимптотою, а на проміжку
20 |
|
|
|
|
;+∞ вона додатна, отже, графік знаходиться над асимптотою. |
|
||
13 |
|
|
Тепер переходимо до побудови графіка. Насамперед, наносимо координатну площину, асимптоти, потім точки максимуму і мінімуму і точку перегину. Знаючи проміжки зростання й спадання функції, а також проміжки опуклості й вгнутості, ми порівняно легко будуємо графік даної
функції (рис. 2.2).
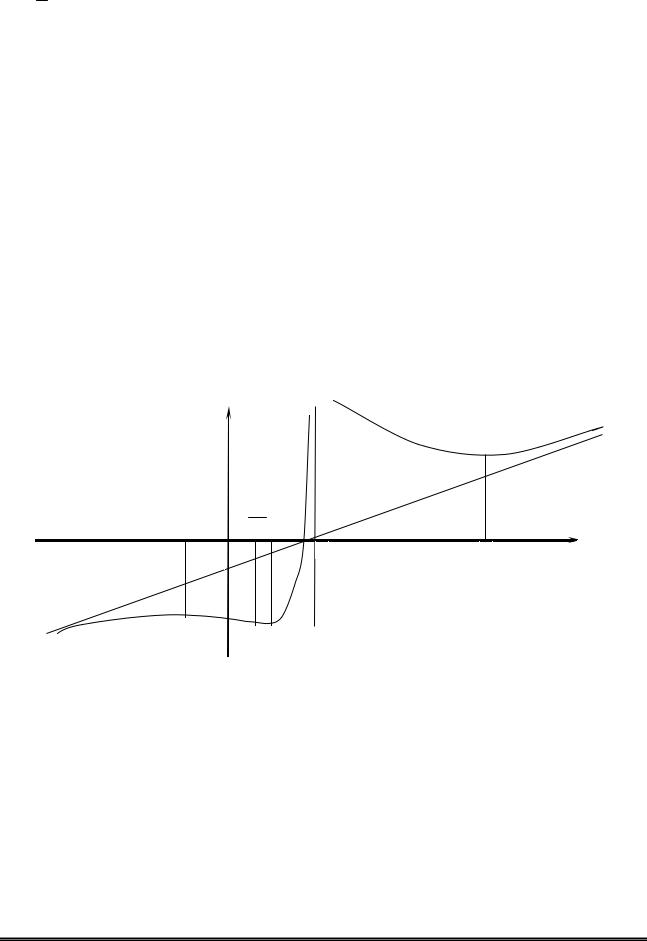
у
|
|
min |
|
8 |
|
|
|
-1 0 13 |
1 |
|
х |
- |
2 |
6 |
|
|
|
max min
Рисунок 2.2 – Графік функції
«Вища математика»

47
2.2 Завдання для самостійної підготовки студентів до модульного контролю
У завданнях №1-№7 необхідно знайти границі, не користуючись правилом Лопіталя.
Завдання №1.
1.1) |
lim |
x3 |
− 2x2 +1 |
|||||||
|
|
x5 − 4 |
|
|||||||
x→∞ |
|
|
||||||||
1.3) |
lim |
− x4 − 2x3 +10 |
||||||||
|
|
x3 − 4x +1 |
||||||||
x→∞ |
|
|
||||||||
1.5) |
lim |
x5 |
−2x2 +1 |
|||||||
|
3x5 −4 |
|
||||||||
x→∞ |
|
|||||||||
1.7) |
lim |
x4 −2x2 +1 |
||||||||
|
|
|
|
|
|
|
|
|
||
x→∞ x6 −4x +12 |
||||||||||
1.9) |
lim |
2x8 −2x5 +1 |
||||||||
|
|
x7 −4 |
|
|||||||
x→∞ |
|
|
||||||||
1.11) |
lim |
|
3x3 −2x2 +1 |
|||||||
|
|
4x3 −4 |
|
|||||||
|
x→∞ |
|||||||||
1.13) |
lim |
|
x5 −11x3 +1 |
|||||||
|
|
|
|
|
|
|
|
|
||
|
x→∞ x4 −4x +6 |
|||||||||
1.15) |
lim |
|
x3 −2x2 +1 |
|||||||
|
|
|
|
|
|
|
|
|
||
|
x→∞ x2 −4x −5 |
|||||||||
1.17) |
lim |
2x5 −11x3 +1 |
||||||||
|
x |
→∞ |
7x5 −4 |
|||||||
1.19) |
lim |
|
x6 − 2x3 + x −3 |
|||||||
|
|
x4 −12 |
||||||||
|
x→∞ |
|||||||||
1.21) |
lim |
|
|
x2 −2 |
|
|||||
|
|
5 −4x +7 |
||||||||
|
x→∞ x |
|||||||||
1.23) |
lim |
|
x4 − 2x2 +1 |
|||||||
|
|
|
|
|
|
|
|
|
||
|
x→∞ −5x4 − 4 |
|||||||||
1.2) |
lim |
x5 |
−2x3 +12 |
|
|||||||||
|
|
3 −4x +3 |
|||||||||||
x→∞ x |
|||||||||||||
1.4) |
lim |
x5 |
−2x2 +1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
x→∞ −2x6 −4 |
|||||||||||||
1.6) |
lim |
2x4 −2x3 +12 |
|
||||||||||
|
|
|
4 −4x3 +3 |
||||||||||
x→∞ 11x |
|||||||||||||
1.8) |
lim |
x5 |
−2x3 + 2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
x→∞ x3 −7x +8 |
|||||||||||||
1.10) |
lim |
|
|
x2 −2 |
|
||||||||
|
|
3 −4x +3 |
|||||||||||
|
x→∞ x |
||||||||||||
1.12) |
lim |
|
x3 |
−2x2 +13 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x→∞ 3x3 −4x +3 |
||||||||||||
1.14) |
lim |
|
x7 +12x4 +1 |
||||||||||
|
|
|
5 −4x +3 |
|
|||||||||
|
x→∞ x |
||||||||||||
1.16) |
lim |
|
x5 |
−2x4 +12 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x→∞ x13 −4x8 +3 |
||||||||||||
1.18) |
lim |
|
3x3 −2x2 +12 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x→∞ 8x3 −4x +3 |
||||||||||||
1.20) |
lim |
|
5x2 −3x +1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x→∞ 3x2 + x −5 |
||||||||||||
1.22) |
lim |
|
5x2 −3x +1 |
|
|||||||||
|
|
|
3 + 4x −5 |
||||||||||
|
x→∞ 3x |
||||||||||||
1.24) |
lim |
|
5x4 −3x +1 |
|
|||||||||
|
|
|
2 +5x −5 |
||||||||||
|
x→∞ 3x |
||||||||||||
ДВНЗ«ДонНТУ» Автомобільно-дорожній інститут

48
1.25) |
lim |
|
6x7 −3x5 +1 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x→∞ 3x2 +9x −5 |
|||||||||||||||||||||
1.27) |
lim |
|
5x2 −3x +1 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x→∞ 3x7 +9x −5 |
|||||||||||||||||||||
1.29) |
lim |
11x2 −3x +1 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x→∞ 18x2 + x −5 |
|||||||||||||||||||||
|
Завдання №2. |
|||||||||||||||||||||
2.1) |
lim |
|
x2 |
−3x + 2 |
|
|||||||||||||||||
|
|
|
|
|
x2 − 4 |
|||||||||||||||||
x→2 |
|
|
|
|
||||||||||||||||||
2.3) |
lim |
|
|
|
x2 |
− x −6 |
|
|||||||||||||||
|
|
|
|
|
x |
2 −9 |
||||||||||||||||
x→3 |
|
|
|
|||||||||||||||||||
2.5) |
lim |
|
|
|
|
x2 |
+ x −20 |
|
||||||||||||||
|
|
|
|
|
x |
2 −16 |
||||||||||||||||
x→4 |
|
|
|
|||||||||||||||||||
2.7) |
lim |
|
|
x2 |
−4x −5 |
|
||||||||||||||||
|
|
|
|
x |
2 −25 |
|||||||||||||||||
x→5 |
|
|
|
|||||||||||||||||||
2.9) |
lim |
x2 |
+ x −6 |
|
||||||||||||||||||
|
|
|
x2 −4 |
|||||||||||||||||||
x→2 |
|
|
|
|||||||||||||||||||
2.11) |
lim |
x2 + 2x −8 |
|
|||||||||||||||||||
|
|
|
x2 −4 |
|||||||||||||||||||
|
x→2 |
|
|
|
||||||||||||||||||
2.13) |
lim |
x2 + x −12 |
|
|||||||||||||||||||
|
|
|
x2 −9 |
|||||||||||||||||||
|
x→3 |
|
|
|
||||||||||||||||||
2.15) |
lim |
x2 + 2x −35 |
|
|||||||||||||||||||
|
|
|
x2 −25 |
|||||||||||||||||||
|
x→5 |
|
|
|
||||||||||||||||||
2.17) |
lim |
|
|
x2 +4x −5 |
|
|||||||||||||||||
|
|
|
|
|
x2 −1 |
|||||||||||||||||
|
x→1 |
|
|
|
||||||||||||||||||
2.19) |
lim |
|
|
x2 − x −2 |
|
|||||||||||||||||
|
|
|
x2 −1 |
|||||||||||||||||||
|
x→−1 |
|||||||||||||||||||||
2.21) |
lim |
x4 −2x3 + x2 |
||||||||||||||||||||
|
|
|
x3 + x2 |
|||||||||||||||||||
|
x→0 |
|
|
|
||||||||||||||||||
1.26) |
lim |
|
|
5x4 −3x +17 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x→∞ 3x2 + x −5 |
|||||||||||||||
1.28) |
lim |
|
|
5x2 −3x +1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x→∞ 3x8 + x7 −15 |
|||||||||||||||
1.30) |
lim |
|
|
4x2 −3x +1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x→∞ 3x2 + x −5 |
|||||||||||||||
2.2) |
lim |
x5 |
−4x4 − x3 |
|
||||||||||||
|
|
|
|
|
x6 − x3 |
|||||||||||
x→0 |
|
|
|
|
|
|||||||||||
2.4) |
lim |
|
x3 |
+ x2 + x |
|
|||||||||||
|
|
|
|
5 − x2 − x |
||||||||||||
x→0 x |
||||||||||||||||
2.6) |
lim |
x4 |
−3x3 − x2 |
|
||||||||||||
|
|
|
|
|
x3 −2x2 |
|||||||||||
x→0 |
|
|
|
|
|
|||||||||||
2.8) |
lim |
|
x4 |
−2x3 + x |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x→0 x8 + x7 − x |
||||||||||||||||
2.10) |
lim |
|
|
x3 −1 |
||||||||||||
|
|
|
|
x −1 |
|
|||||||||||
|
x→1 |
|
|
|||||||||||||
2.12) |
lim |
|
x3 −8 |
|
||||||||||||
|
|
x −2 |
||||||||||||||
|
x→2 |
|
|
|||||||||||||
2.14) |
lim |
|
|
x3 −1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x→1 x2 −1 |
|||||||||||||||
2.16) |
lim |
|
x2 −4 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x→2 x3 −8 |
|||||||||||||||
2.18) |
lim |
|
|
|
|
x2 −9 |
|
|||||||||
|
|
|
|
|
3 −27 |
|||||||||||
|
x→3 x |
|||||||||||||||
2.20) |
lim |
|
x2 −4x + 4 |
|
||||||||||||
|
|
|
x3 −8 |
|||||||||||||
|
x→2 |
|
|
|
||||||||||||
2.22) |
lim |
|
x2 −4x + 4 |
|
||||||||||||
|
|
|
x2 −4 |
|||||||||||||
|
x→2 |
|
|
|
||||||||||||
«Вища математика»

2.23) |
lim |
x2 −6x +9 |
|
|||||||||||||
|
|
|
x3 −27 |
|||||||||||||
|
x→3 |
|
|
|
||||||||||||
2.25) |
lim |
|
|
|
|
x3 |
|
−1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x→1 x2 −2x +1 |
|||||||||||||||
2.27) |
lim |
|
|
|
x3 −125 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x→5 x2 −10x + 25 |
|||||||||||||||
2.29) |
lim |
|
x2 −6x +8 |
|
||||||||||||
|
|
|
x |
−2 |
||||||||||||
|
x→2 |
|
|
|
||||||||||||
|
Завдання №3. |
|||||||||||||||
3.1) |
|
|
2x −1 x |
|||||||||||||
lim |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||||||
x→∞ 2x + |
1 |
|||||||||||||||
3.3) |
x −1 |
2x |
||||||||||||||
lim |
|
|
|
|
|
|||||||||||
|
|
|
|
|||||||||||||
x→∞ x +1 |
|
|||||||||||||||
|
x −4 x |
|||||||||||||||
3.5) |
lim |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
||||||||||||
x→∞ x +5 |
||||||||||||||||
3.7) |
|
|
2x + 4 x |
|||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||
x→∞ 2x + |
1 |
|||||||||||||||
3.9) |
|
|
3x +5 x |
|||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||
x→∞ 3x + |
1 |
|||||||||||||||
3.11) |
lim |
5x +11 x |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||
|
x→∞ 5x |
+1 |
||||||||||||||
3.13) |
lim |
21x −10 x |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
x→∞ 21x +1 |
|||||||||||||||
3.15) |
lim |
x +3 2x |
||||||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
||||||||||||
|
x→∞ x − |
1 |
||||||||||||||
3.17) |
lim |
x −1 x |
||||||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
||||||||||||
|
x→∞ x + |
1 |
||||||||||||||
3.19) |
lim |
2x + 4 x |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||||||
|
x→∞ 2x +1 |
|||||||||||||||
49
2.24) |
lim |
|
x2 |
−12x +36 |
|
|||||
|
|
|
|
x −6 |
||||||
|
x→6 |
|
|
|
||||||
2.26) |
lim |
|
|
x2 +16x +64 |
||||||
|
|
|
x +8 |
|||||||
|
x→−8 |
|
||||||||
2.28) |
lim |
|
|
|
x2 −12x + 20 |
|
||||
|
|
|
|
x −10 |
||||||
|
x→10 |
|
||||||||
2.30) |
lim |
|
x2 |
−4x +3 |
||||||
|
|
|
|
|
x −3 |
|
||||
|
x→3 |
|
|
|
|
|||||
3.2) lim 7x −8 x x→∞ 7x +9
x −15 x
3.4) lim x→∞ x +16
x −10 x
3.6) lim x→∞ x +11
3.8) lim x +1 4x x→∞ x −1
3.10) |
x + 7 |
2x +4 |
|
lim |
|
|
|
|
|||
|
x→∞ x +5 |
|
|
|
|
2x − |
1 |
2x −4 |
||||
3.12) |
lim |
|
|
|
|
|
|
|
|
|
1 |
||||||
|
x→∞ 2x + |
|
||||||
3.14) |
x −1 |
x −5 |
||||||
lim |
|
|
|
|
|
|||
|
|
|
|
|||||
|
x→∞ x +1 |
|
|
3x +2 |
||||
3.16) |
x − 4 |
|||||||
lim |
|
|
|
|
|
|||
|
|
|
|
|||||
|
x→∞ x +5 |
5x −7 |
||||||
|
|
2x + |
4 |
|||||
3.18) |
lim |
|
|
|
|
|
|
|
|
|
1 |
||||||
|
x→∞ 2x + |
|
||||||
3.20) |
|
3x + |
5 |
|
3x −7 |
|||
lim |
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||
|
x→∞ 3x + |
|
|
|||||
ДВНЗ«ДонНТУ» Автомобільно-дорожній інститут

50
|
|
5x +11 x +4 |
||||||
3.21) |
lim |
|
|
|
|
|
||
|
|
|
|
|||||
|
x→∞ |
5x +1 |
||||||
3.23) |
|
21x −10 3x −7 |
||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x→∞ |
21x +1 |
||||||
3.25) |
x +3 x −8 |
|||||||
lim |
|
|
|
|||||
|
|
|||||||
|
x→∞ x −1 |
|||||||
3.27) |
x −1 3x +5 |
|||||||
lim |
|
|
||||||
|
||||||||
|
x→∞ x +1 |
|||||||
3.29) |
|
2x + 4 −2x −7 |
||||||
lim |
|
|
|
|
||||
|
|
|
||||||
|
x→∞ |
2x +1 |
||||||
Завдання №4.
4.1) |
lim |
1−cos x |
|
|
|
|
|
|
|||||
|
|
5x2 |
|||||||||||
x→0 |
|
|
|
||||||||||
4.3) |
lim |
arcsin 3x |
|
|
|
|
|||||||
|
5x |
||||||||||||
x→0 |
|
|
|
||||||||||
4.5) |
lim |
|
|
arctg 3 x |
|
||||||||
|
|
|
4x3 |
||||||||||
x→0 |
|
|
|
||||||||||
4.7) |
lim |
|
|
1−cos8x |
|
||||||||
1−cos16x |
|||||||||||||
x→0 |
|||||||||||||
4.9) |
lim |
|
|
sin 4πx |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
x→0 sin12πx |
|||||||||||||
4.11) |
lim |
arc sin 4πx |
|||||||||||
|
|
|
|
|
|
|
|
||||||
|
x→0 arc sin 24πx |
||||||||||||
4.13) |
lim |
sin 2 4x |
|||||||||||
|
|
|
|
|
|
|
|
||||||
|
x→0 sin 2 12x |
||||||||||||
4.15) |
lim |
tg 2πx |
|||||||||||
|
|
|
|
|
|
|
|
||||||
|
x→0 x2 |
||||||||||||
4.17) |
lim |
arctg4x |
|
||||||||||
2x |
|||||||||||||
|
x→0 |
||||||||||||
4.19) |
lim |
sin 4 5x |
|
||||||||||
x4 |
|||||||||||||
|
x→0 |
||||||||||||
3.22) |
7x −8 4x |
||||||||
lim |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||||
|
x→∞ 7x +9 |
||||||||
3.24) |
x −15 |
3x +15 |
|||||||
lim |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||||
|
x→∞ x |
+16 |
7x −1 |
||||||
3.26) |
x |
−10 |
|||||||
lim |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||||
|
x→∞ x +11 |
|
|||||||
3.28) |
x |
+1 3x +2 |
|||||||
lim |
|
|
|
|
|||||
|
|
|
|||||||
|
x→∞ x |
−1 |
|
||||||
3.30) |
x |
+ 7 x −4 |
|||||||
lim |
|
|
|
|
|
||||
|
|
|
|
||||||
|
x→∞ x +5 |
|
|||||||
4.2) |
lim |
|
|
sin x |
||||||||
|
|
|
|
|
|
|
|
|
|
|||
x→0 sin 8x −sin 3x |
||||||||||||
4.4) |
lim |
arcsin 6x |
|
|
|
|
|
|||||
|
|
|
|
|||||||||
x→0 arcsin 3x |
||||||||||||
4.6) |
lim |
1 −cos8x |
|
|
|
|
||||||
|
x2 |
|||||||||||
x→0 |
||||||||||||
4.8) |
lim |
|
|
2x2 |
|
|||||||
|
−cos16x |
|||||||||||
x→01 |
||||||||||||
4.10) |
lim |
sin 8x + x |
|
|||||||||
x |
||||||||||||
|
x→0 |
|||||||||||
4.12) |
lim |
1−cos x |
|
|
|
|||||||
x2 |
||||||||||||
|
x→0 |
|||||||||||
4.14) |
lim |
x2 |
||||||||||
|
|
|
|
|
|
|
|
|||||
|
x→0 tg 2 2x |
|||||||||||
4.16) |
lim |
arcsin 5x |
|
|||||||||
10x |
||||||||||||
|
x→0 |
|||||||||||
4.18) |
lim |
sin3 5x |
||||||||||
|
|
|
|
|
|
|
|
|||||
|
x→0 10x3 |
|||||||||||
4.20) |
lim |
1−cos 4x |
|
|||||||||
2xtgx |
||||||||||||
|
x→0 |
|||||||||||
«Вища математика»
