МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Методические указания

ПО ДИСЦИПЛИНЕ

"ДИСКРЕТНАЯ МАТЕМАТИКА"

для студентов специальностей

7.091501: "Компьютерные системы и сети"

7.091502: ”Системное программирование”

направления подготовки 0915 «Компьютерная инженерия»

Утверждено

на заседании кафедры КИ

протокол № ___

от ______________

Рекомендовано до видання

методичною комісією

спеціальностей 7.091501 і 7.091502

Протокол № від

Донецк 2013

УДК 681.973

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ДИСЦИПЛИНЕ «ДИСКРЕТНАЯ МАТЕМАТИКА» (для студентовза напрямом підготовки 6.0915 «Комп'ютерна інженерія», спеціальністі 7.091501 - "Комп'ютерні системи та мережі") .

Составитель: Чередникова О.Ю.

Ответственный

за выпуск: В.В.Лапко

Л И Т Е Р А Т У Р А

1. Дискретная математика для программистов / Ф.А. Новиков – СПб: Питер, 2001.

2. Виленкин Н.Я. Комбинаторика. – М.: Наука, 1969.

3. Холл М. Комбинаторика. – М.: Мир,1970.

4. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженеров. – М.: Энергия, 1980.

5. Столл Р. Множества. Логика. Аксиоматические теории. - М.: Наука, 1968.

6. Яблонский С.В. Введение в дискретную математику. - М.: Наука, 1979.

7. Кофман А. Введение в прикладную комбинаторику. - М.: Наука, 1975.

8. Липский В. Комбинаторика для программистов. - М.: Мир, 1988.

9. Кнут Д. Мистецтво програмування / т.1, 2, 3 /. – М.: Мир, 1976 – 1978.

Содержание

Лабораторная работа №1

Лабораторная работа №2

Лабораторная работа №3

Лабораторная работа №4

Теоретические вопросы по модулю 1 «Теория множеств»

Лабораторная работа №5

Лабораторная работа №6

Теоретические вопросы по модулю 2 «Графы» Лабораторная работа №1

Цель: Освоить основные операции над множествами.

Тема: Операции над множествами

Задание 1Задание 2Задание 3

Теоретические сведения

Понятию множества нельзя дать строгого определения. Более общего понятия, чем множество в математике не существует. Это - "совокупность, собрание, класс, семейство". Часто множество - несколько объектов, объединенных общим признаком.

Предметы, составляющие множество, называются элементами. Для указания того, что множество А состоит из элементов х, у ...z пишут А={ х,у.... }. Например: множество арифметических действий состоит из элементов { сложения, вычитания, умножения, деления }. Tо, что элемент хпринадлежитмножеству А, записывают xA. Если не принадлежитxA.

Например: если А - множество натуральных чисел, то 6 А, а вот 1.3А.

Операции над множествами

Объединением (суммой)множеств А и В называется множество, каждый элемент которого принадлежит хотя бы одному из множеств А и В. (Обозначение АВ={x x Aили x B})

Пусть А={ 1,2,3 }; В={ 1,2,4,5 }; A В={ 1,2,3,4,5 }.

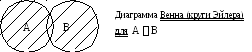
Пересечением (произведением)множеств А и В называется множество, каждый элемент которого принадлежит одновременно А и В (обозначается АВ={x x Aи x B}).

П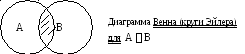усть А={ 1,2,3 }; B={1,2,4,5}; АВ={ 1,2 }.

Разностьюдвух множеств А и В (относительным дополнением), называется новое множество А-В или А/В в которое входят все элементы множества А не принадлежащие В.A - B = {x xAи xB}. Совсем не обязательно, чтобы множество А было частью множества В.

П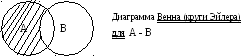ример: A={1,2,3,4} B={1,3,5} A-B={2,4} B-A={5}

Симметрической разностьюдвух множеств А и В, называется новое множество АΔВ, в которое входят все элементы множества А-В и В-А.

AΔB = {x (xAи xB)или(xВи xА) }.

П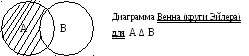ример:A={1,2,3,4}B={1,3,5}AΔB={2,4,5}