Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донецкий национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

matem_2_chast.pdf

Скачиваний:

Добавлен:

03.03.2016

Размер:

1.44 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 55

Задание 8.5. Исследовать на непрерывность функцию, построить ее график (см. табл. 8.5):

Таблица 8.5

Номер

варианта

x +1, x ≤1,

− x, x < 0,

y =

+3, 0 ≤ x < 2,

2x2 , 1 < x ≤3,

, x

≥ 2;

1, x >3;

−1, x < 0,

−3, x < −1,

y =

2x +1, 0 ≤ x ≤1,

y =

−3 − x, −1 < x ≤1,

x >1;

x ≤ −1,

2x +5, x ≤ 0,

y =

+ 2, −1 < x < 0,

y =

2 +5, 0 < x ≤3,

, x

≥ 0;

1, x >3;

−

< −

−

2, x

y =

+1, − 2 < x <1,

y =

x, 1 < x <3,

2x, x >1;

2x −3, x >3;

−

< −

3 − 2x, x ≤ 0,

y =

2 +3, 0 < x ≤1,

2x −1, −1 < x <1,

x >1;

x, x < 0,

1, x < −1,

y =

3x2 , 0 ≤ x < 2,

y =

x2 +1, −1 ≤ x < 2,

2x −3, x > 2;

2x +1, x > 2;

3, x < −1,

2x −3, x <1,

y =

2 +1, −1 ≤ x <1,

y =

−2, 1 < x < 2,

+1, x ≥1;

x ≥ 2;

x +1, x ≤ 0,

x < −1,

−x

y =

1, 0 < x < 2,

y =

2x −3, −1 ≤ x ≤ 2,

−1, x > 2;

x > 2;

Окончание табл. 8.5

x < −1,

−3, x ≤ −2,

y =

− x, −1 ≤ x < 0,

y = 2x + 4, − 2 < x ≤1,

− х, x >1;

3x + 2, x ≥ 0;

−1, x ≤ −2,

3x −1,

x < 0,

y =

2 −1, 0 ≤ x ≤1,

2x +1, − 2 < x ≤1,

y = x

x >1;

x < 0,

x < −3,

y =

− x, −3 ≤ x <1,

x, 0 < x <3,

y = 2

2x −3, x >3;

1, x >1;

+5, x ≤ −1,

−

2x, x

≤ −

y =

3x +1, −1 < x ≤ 2,

+3, − 2 < x ≤1,

y = x

x > 2;

2x + 2, x >1;

x −1, x ≤1,

+1,

x < −1,

y =

+3, 1 < x ≤ 2,

y = x +3, −1 ≤ x < 2,

4x −1, x > 2;

1, x > 2;

2x, x < −3,

− x, x ≤3,

− x, −3 ≤ x ≤ 0,

y = 3

y = 1, 3 < x ≤ 4,

3, x > 0;

2х−7, x > 4;

0, x ≤ 2,

y =

−1, x ≤ −1,

x +1, −1 < x ≤ 0,

y = 2x −4, 2 < x ≤3,

x > 0;

x >3.

РАЗДЕЛ 4

ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ

ТЕМА 1

ПРОИЗВОДНАЯ ФУНКЦИИ

Понятие производной

Пусть функция y = f (x) определена и непрерывна на некотором интервале (a, b) . Производной функции f (x) по независимой переменной x называется предел отношения приращения функции ∆y к приращению аргумента ∆x , когда приращение аргумента стремится к нулю, т.е.

lim	f (x + ∆x) − f (x)				= lim		∆y			′
										′
		∆x					∆x		= f (x) .
∆x→0		∆x				∆x→0	∆x
Если этот предел конечен, то функция										y = f (x) называется дифференци-
руемой в точке x . Если				′		то говорят, что функция y = f (x) имеет в
руемой в точке x . Если			f (x) = ∞,			то говорят, что функция y = f (x) имеет в
точке x бесконечную производную.									f ′(x) или dy .
Производная обозначается y′= y′(x),									f ′(x) или dy .
										dx
Операция нахождения производной называется дифференцированием.
Число
f+′(x) =		lim	f (x + ∆x) − f (x)
f+′(x) =		lim		∆x
		∆x→+0		∆x
называется правосторонней производной в точке x . Число
f−′(x) =		lim	f (x + ∆x) − f (x)					.
f−′(x) =		lim						.
		∆x→−0		∆x
называется левосторонней производной в точке x .
Производная f		′	функции			y = f (x)				существует тогда и только тогда,
Производная f		(x)	функции			y = f (x)				существует тогда и только тогда,

когда f−′(x) = f+′(x) .

Дифференцирование явно заданных функций

Основные правила дифференцирования

1)C′= 0 , где C – постоянная величина;

2)(u(x) ±v(x))′=u′(x)±v′(x);

3)(u(x) v(x))′ =u′(x) v(x)+v′(x) u (x);

4)(сu(х))′ = с(u(х))′, C – постоянная величина;

5)u(x) ′ = u′(x)v(x)(−)u2(x)v′(x), v(x) ≠ 0 ;

v(x) v x

6) если функция u =ϕ(x) дифференцируема в точке x0 , а функция y = f (u) дифференцируема в точке u0 =ϕ(x0 ) , то сложная функция y = f (ϕ(x)) дифференцируема в точке x0 и y′x (x0 ) = yu′(u0 )u′x (x0 ) .

Таблица производных основных элементарных функций

y =C

y′=0

y = x

y′=1

y = xn

y′= nxn−1

y =un

y′= nun−1u′

y = x

y′ =

y = u

y′ =

u′

y =logах

y′ =

y =loga u

y′ =

u′

xln a

u ln a

y = lnх

y′=

y = ln u

y′ = u′

y = ax

y′ = ax ln a

y = au

y′ = au ln a u′

y = ex

y′ = ex

y = eu

y′ = eu u′

y =sin x

y′= cos x

y =sin u

y′= cosu u′

10.

y = cos x

y′= −sin x

y = cosu

y′= −sin u u′

11.

y = tgx

y′=

y = tgu

y′=

u′

cos2 x

cos2 u

y = ctgx

y = ctgu

u′

12.

y′= −

sin2 x

sin2 u

13.

y = arcsin x

y′=

y = arcsin u

y′=

′

1− x2

1−u2

14.

y = arccos x

y′= −

y = arccosu

y′= −

′

1− x2

1−u2

15.

y = arctgx

y′ =

y = arctgu

y′ =

u′

1 + x2

1 +u2

16.

y = arcctgx

y′ = −

y = arcctgu

y′ = −

u′

1 + x2

1 +u2

Производные высших порядков.

Формула Лейбница

Если производная (n −1) – го порядка функции y = f (x) уже определена,

то производная n – го порядка определяется равенством y(n) (x) = y(n−1) (x) ′. В

частности y′′(x) =[y′(x)]′, y′′′(x) =[y′′(x)]′ и т.д.

Если u(x) и v(x) – n раз дифференцируемые функции, то

[c1u(x) + c2v(x)](n) = c1 [u(x)](n) + c2 [v(x)](n) ,

где c1, c2 – произвольные постоянные.

Для произведения u(x) v(x) справедлива формула Лейбница

[u v](n) = u(n)v + nu(n−1)v′+ n(1n −21) u(n−2)v′′+... +uv(n) =

= ∑Cnku(n−k )v(k ) . k =0

Верны следующие формулы:

1)(xm )(n) = m(m −1)...(m −n +1)xm−n ;

2)(ax )(n) = ax lnn a, (a > 0) , в частности (ex )(n) =ex ;

3)(ln x)(n) = (−1)n−1 (nx−n1)!;

4)(sin x)(n) =sin x + πn ;

5)(cos x)(n) = cos x + πn .

Дифференцирование обратных функций и функций, заданных неявно или параметрически

(4.1)

(4.2)

(4.3)

Пусть функция y = f (x) ( a < x < b ) дифференцируема и имеет однозначную непрерывную обратную функцию x = g( y) и y′x ≠ 0, то обратная функция также дифференцируема и

x′y = 1 . y′x

В частности для производной второго порядка имеет место равенство

x′′yy = −	y′xx′	.
	( y′x )2

Пусть дифференцируемая функция задана неявно уравнением F (x, y) = 0 . Для вычисления производной надо продифференцировать уравнение F (x, y) = 0

по переменной x и полученное уравнение		d	F(x, y) = 0 решить относительно y′x .
по переменной x и полученное уравнение		dx	F(x, y) = 0 решить относительно y′x .
		dx
Пусть однозначная непрерывная функция от переменной x задана систе-
мой уравнений
y =u(t),	α <t < β,
	α <t < β,
x = v(t),

где u(t) и v(t) – дифференцируемые функции и также существует и определяется равенством

y′ = du : dv = ut′ = yt′ . x dt dt vt′ xt′

v′(t) ≠ 0 . Тогда производная y′x

(4.4)

Производные высших порядков вычисляются последовательно. В частности, производная второго порядка вычисляется по формуле:

y′′xx = xt′ytt′′ − xtt′′yt′ . (xt′)2

Примеры решения задач

Пример4.1. Найтиприращение ∆y функции y = x2 при x = 0 и ∆x = 0,001.

Решение. ∆y = (x +∆x)2 − x2 = 0,000001.

Пример 4.2. Исследовать дифференцируемость функции y = 3 x −1 в точ-

ке x =1.

Решение. При x =1 приращение функции имеет вид:

∆y = 3 (1+∆x) −1 − 3 1 = 3 ∆x −1.

Тогда

lim	∆y	= lim	3 ∆x −1	= ∞.
	∆x		∆x
∆x→0		∆x→0

Следовательно, в точке x =1 функция y = 3 x −1 не имеет конечной про-

изводной.

Пример 4.3. Исследовать дифференцируемость функции y = arccos(sin x) .

Решение.

′

cos x

1−sin2 x =

cos2 x

= | cos x | .

Следовательно,

y′=1,

если

cos x > 0 ;

y′= −1, если cos x < 0 .

В точках

x = π

+πk , (k = 0, ±1,± 2,...) ,

где cos x = 0 , функция непрерывна,

но не диффе-

ренцируема.

Пример 4.4. Пользуясь определением производной, найти производную

функции

f (x) = x2

в точке

=3.

Решение. Найдем приращение функции f (x) = x2

в точке x

∆y = f (3 +∆x) − f (3) = (3 +∆x)2 −32 = 6∆x +(∆x)2 .

Тогда

lim

∆y

= lim 6∆x −(∆x)2

= lim

(6 + ∆x)= 6 .

∆x→0

∆x

∆x→0

∆x

∆x→0

′

=6 .

Таким образом, y (3)

Пример 4.5. Доказать, что (tgx)′

cos2 x

sin x

′

Решение. Так как tgx = cos x ,

(sin x)

= cos x , (cos x)

=sin x , то

′

sin x

(sin x) cos x −sin x(cos x)

(tgx) =

cos

cos x

cos2

x +sin2 x

cos2 x

cos2

Пример 4.6. Найти производные следующих функций:

y = x2 −

+sin x + log5 x ;

y =5x cos(2x +3) ;

y =

y =sin

;

+ x

Решение.

′

− 1

− 3

y′= x

− 2x

2 +sin x

+ log5

= 2x + x 2 + cos x

;

xln 5

y′ =(

5x cos(2x +3))′ = (

5x )′ cos(2x +3) +5x (cos(2x +3))′ =

x2cos2 (1/ x)

=5x ln 5 cos(2x +3) −5x sin(2x +3)(2x +3)′ =

=5x ln5 cos(2x +3) −5 2x sin(2x +3) .

′

x ′

) −e

+ x

′

) −

3) y′ =

)

(1 + x

)

(1 + x

1 + x

)

(1 + x

ex (x3

−3x2 +1)

+ x3 )2

′

y′= sin

2sin

cos

−

cos

(1/ x)

= −sin (2tg(1/x)).

Пример 4.7. Найти производную второго порядка для функции y = e−x2 . Решение. Находим производную первого порядка:

y′ = (e−x2 )′ = e−x2 (−x2 )′= −2xe−x2 .

Теперь находим производную второго порядка:

y′′ =(−2xe−x

)′

= −2

+ x (e−x

)′

= −2(e−x

))=

x′ e−x

+ x (−2xe−x

−x2

(

)

−x2

(

)

= −2e

1 − 2x

= 2e

−1 .

Пример 4.8.

Применяя

формулу

Лейбница,

найти

y(20) для функции

y = x2 cos x .

Решение. Так как (x2 )(n) =0 при n ≥3 , то из (4.1) имеем

(20)

=(x

cos x)

(20)

=(cos x)

(20)

+ 20

(cos x)

(19)

′

)

+ 20219 (cos x)(18) (x2 )′′,

Отсюда и равенств (4.2), (4.3)

(20)

= x

+ 20

+19

380cos

+18

cos x

+ 40xcos x

=(x2 −380)cos x + 40xsin x .

Пример 4.9. Найти производную функции y = xcos x .

Решение. Первый способ. Так как y = eln xcos x = ecos x ln x , то

y′= e

cos x ln x

(cos x ln x)′ = e

cos x ln x

cos x

−sin x ln x +

= x

cos x

−sin x ln x .

Второй способ. Рассмотрим логарифм заданной функции:

ln y = ln xcos x						ln y = cos xln x .
Дифференцируя обе части по переменной									x и считая, что функция
ln y(x) является сложной функцией, получаем
1		y′ =	cos x		−sin x ln x .
	y	y′ =		x	−sin x ln x .
Следовательно,
	y′= y		cos x				cos x cos x
	y′= y			x		−sin x ln x = x		x	−sin x ln x .
				x				x

Пример 4.10. Для функции

x =5(t −sin t),y =5(1 −cost),

заданной параметрически, найти производную первого порядка от y по пере-

менной x .

Решение. Находим производные от y и x по переменной t :

xt′ =5(1−cost); yt′ =5sin t .

Тогда из (4.4) следует, что

dy	=	5sin t	= ctg	t	(t ≠ 2πk, k = 0,±1,±2,...) .
dx		5(1 −cost)
			2

Задания для самостоятельного решения

4.1. Найти приращение функции y = x2 + 2 в точке x =1 при: 1) ∆x = 0,01; 2) ∆x = −0,3 .

4.2. Найти приращение функции y = x − x2 в точке x = 0 при: 1) ∆x = 0,001; 2) ∆x = −0,5 .

4.3.Пользуясь определением производной, найти производную функции

вкаждой точке ее области определения, если;

1)	y = x3 ;	2)	y = cos 2x ;				3)	y =	x, x > 0 ;
4)	y =sin 4x ;	5)	y = x2 + x3 ;				6)	y =	x −1, x >1;
7)	y = x3 + 2 ;	8)	y =		1	;	9)	y =log2 x ;
					x + 2
				1					1 +1.
10) y =3x ;		11)			;		12) y =
				x2
									x

4.4. Пользуясь определением, найти производную функции в заданной точке x0 :

1)	y = 2 − x, x =1;												2)	y = x2 + 2, x =0;
							0															0
3)	y = x2 − x,							x =1;					4)	y =sin 2x,								x		=π / 4;
							0															0
5)	y =cos x,						x =π / 2;						6)	y = 2x ,					x			=1;
							0													0
																	2	,				x ≥		0,
7)	y = ctgx, x0 =π / 4;												8)		x			,				x ≥		0,		x0	= 0.
7)	y = ctgx, x0 =π / 4;												8)	y =						,		x <		0,		x0	= 0.
															−x4					,		x <		0,

4.5. Найти производные следующих функций:
1)	y =		x3	−		x4		+ x2	;				2)	y = x − 3 x + 4 x;
1)	y =			−				+ x2	;				2)	y = x − 3 x + 4 x;
		3			4
3)	y =(1+ 2x)2 ;												4)	y = (x + x)3 ;
5)	y = 2x			+3x			−4−x		+3x 5x ;				6)	y =ln x +log2 x −2log3 x;
7)	y =sin x +						4cos x −				1 ;		8)	y = tgx +3ctgx ;
											x					1					1				1
9)	y = 4x5 −							2x ;					10)		y =	1		−			1		−		1	;
9)	y = 4x5 −							2x ;					10)		y =	x		−					−		x3	;
		y =5x														x					x2				x3
11)		y =5x			−log2 3x ;								12)		y = 5 x −cos(3x +1) + tg3x ;
13)		y = 2x			+ ln 4x −					1		;	14)		y = (1+ 2x)50 ;
13)		y = 2x			+ ln 4x −							;	14)		y = (1+ 2x)50 ;
			4x							2x
15)		y = arcsin x −ex cos x ;											16)		y = ex sin x ;
		y = x		2	arcsin3x ;										y =	1						x +			1 2			x		1	2	5
17)													18)													−			−			;
17)													18)													−			−			;
																x	5													x
																x									x					x
															42

19)	y = (1+ x2 )ln(1− x) ;
21)	y = (x2 + x)cos(3x −1) ;
23)	y =	x2 ln x					;
		1	+ x2

25)	y = tgx −ctgx ;
		tgx +ctgx
27)	y =		x sin x					;

			x		4x				x
29)	y =sin			2 2			+cos2			;
					x
								2
31)	y =	ex −e−x						;
		ex +e−x

33)	y = log				2	1 −sin 2x ;
						1 +sin 2x
35)	y = ln (ex					+ 1 + e2 x );
37)	y = 3		x + 3 x + 3 1+ x2 ;

20)

y = 2x arccos 2x ;

22)

y = 5

x2 log3 (x −1) ;

24)

y =

;

− 3

3x+1

26)

y =

arctgx

;

2x + x2

28)

y =

(1 + 2x)2

;

30)

y = ln 1 − x2

1 + x2 ;

32)

y = ln tg

−cos xln tgx ;

34)

y = arctg

;

1− x2

36)

y = ex + ee

+ e

;

38)

y =

−arcctgx6 ;

1 + x

y = arctg (x + 1 + x

);

y = ln

−x2

39)

40)

arccos

;

log

( x2

+x+1)

41)

y =3 9

;

42); y = x

arcsin

x +

x2 cos x

43)

y = arcsin

sin2 x

;

44)

y = ln

x +1 +5

+ln

+ln x .

4.6. Пользуясь логарифмическим дифференцированием, найти производные следующих функций:

y = x1/ x ;

y = logx 2 +logx2 (x2 +1) ;

y = xcos x ;

y = xxx ;

y = (cos x)sin x ;

y =(

tgx )x+1 ;

y = 3

x3 (x2 +1)

;

y = 3

sin 2x

;

5 − x

1 −sin 2x

y =

x + 2

;

10) y =

7 x3 4

x −1

(x2

+ 2x)3

, x >1.

3 (x

−1)2 (x + 4)3

x +1

4.7. Исследовать на дифференцируемость функции:

y = 1 −

1 − x2 ;

y =| x | sin x ;

y = x | sin x |;

y = x2 | x |;

, x

0 , x ≥ 0,

y =

;

y =

≤ 0;

x2 , x < 0.

x4 , x

4.8. Найти правую и левую производные в точке x0 :

y =| x +1|,

= −1

;

y = x2 −1,

x = 2

;

y =

x, x ≥ 0,

= 0;

ex , x ≥ 0,

x0 = 0;

x < 0,

y =

5x,

cos x, x < 0,

y =| sin x |,

x0 =π ;

y =| x | −| x +1|, x0 =0 ;

y =| x2 − x |,

;

y =

sin2 x −sin x,

x =π ;

y = tgxctgx,

x0 =π / 4 ;

10)

y =arcsin(sin x),

x0 =π / 2 .

4.9. Подобрать коэффициенты a и b так, чтобы функция

f (x)

была не-

прерывной и дифференцируемой в точке x = x0 , если

, x ≤ x ,

+bx +1, x ≥ x ,

f (x) =

= 0.

ax +b, x > x ;

+ a)e−bx ,

x < x ,

4.10. Применяя формулу Лейбница, найти производные указанных по-

рядков для функций:

y = уx (x2 +1),

y = x2 sin x,

найти y(25) ;

найти y(20) ;

y = x3 cos x,

найти y(10) ;

y = e−x cos x,

найти y(5) ;

y = (2x2 −1)sin x,

найти y(6) ;

y = (1−e−x )sin x, найти y(10) .

4.11. Найти производные второго порядка следующих функций:

y =

−

−5x2 +

;

y =1 + x2 ;

x +3

y =

cos3x

;

y =(sin 2x +cos5x)

x ;

2 −ln x

y = arcsin x

;

y = e−x2 ;

1 − x2

y =3x arcsin 2x ;

y = x3 cos2x ;

y =

;

10)

y =5 x ;

sin 3x

11) y =5etg5x ;

12)

y = ln3 (x +1) .

4.12. Пользуясь правилом дифференцирования обратной функции, найти

указанные производные:

y = 4 x,

найти

y′x ;

y = arccos

найти y′x ;

y = ln

1 + x,

найти

y′x ;

y = 2x3 +3x2 ,

найти x′y ;

y = cos x + 2x,

найти

x′′yy ;

y = x2 +e2 x ,

найти

x′′yy .

4.13. Дляфункций, заданныхпараметрически, найтиуказанныепроизводные:

x = 5sin t +sin 5t ,

y =5cost −cos5t , найти

y′x ;

x =e2t ,

y =e−2t ,

найти

y′x ;

x = 2cos3 t,

y = 2sin3 t ,

найти

y′xx′ ;

x = et cost,

y = et sin t ,

найти y′xx′ ;

−t

′′′

x =e

y =t

найти yxxx ;

x = arcsin t,

y =

1 −t2 ,

найти y′xx′ ;

x =t2 −3,

y =t3 −t ,

найти y′xx′ ;

x =ln(1+t2 ),

y = t − arctgt ,

найти y′x .

4.14. Для неявно заданных функций найти y′x :

x2 + xy + y2 = 0 ;

2) x3 − y2 −4x +5y −3 = 0 ;

3) ln x +e

−

4) xy + x + y −2 = 0 ;

x =5 ;

+ y

6) e

sin x +e

cos y = 0 ;

arctg

= ln

;

arctgy − y + x2 = 0;

8) ex

+ x =ey + y ;

x − y = ex+y ;

10) ey + xy = e .

ТЕМА 2

ДИФФЕРЕНЦИАЛ ФУНКЦИИ

Если приращение функции ∆y может быть представлено в виде:

∆y = f (x +∆x) − f (x) = A(x)∆x +α(x,∆x)∆x ,

где lim α(x, ∆x) = 0 , то функция y = f (x) называется дифференцируемой в точке

∆x→0

x . Главная линейная часть A(x)∆x называется дифференциалом функции и обозначается df (x) или dy . Дифференциал функции существует тогда и только тогда, когда существует конечная производная y′= A(x) . Дифференциал функции можно записать следующим образом:

∆y = y′dx = f ′(x)dx .

Если ∆x достаточно мало, то с точностью до бесконечно малых более высокого порядка, чем ∆x , справедлива приближенная формула ∆y ≈ dy . Кро-

ме того, из (4.5) следует, что ∆x = x .

Дифференциалы высоких порядков последовательно определяются по формулам:

d 2 y = d(dy), d3 y = d(d 2 y),..., d n y = d(d n−1 y) .

Примеры решения задач

Пример 4.11. Найти дифференциал функции у = ln(x2 +3x +3) +sin 2x .

Вычислить dy при x = 0 , ∆x = 0,01.
Решение.
	2	′			2x +3
dy =(ln(x		+3x +3) +sin 2x)	dx =			+ 2cos 2x dx .
dy =(ln(x		+3x +3) +sin 2x)	dx =	2	+3x +3	+ 2cos 2x dx .
			x		+3x +3

Подставив x = 0 и dx = ∆x = 0,01, находим

dy =(1+ 2) 0,01 = 0,03.

Пример 4.12. Найти приращение и дифференциал функции y =3x2 −2x +5 в точке x =1 при ∆x = 0,1. Найти абсолютную и относительную

погрешности, которые допускаются при замене приращения функции ее дифференциалом.

Решение. По определению

∆y = y(x + ∆x) − y(x) =3(x + ∆x)2 − 2(x +∆x) +5 −(3x2 − 2x +5) =

=3∆x2 +6x∆x − 2∆x

dy = y′(x)dx = (6x −2)dx = (6x −2)∆x .

Тогда

∆y −dy =3∆x2 +6x∆x −2∆x −6x∆x + 2∆x =3∆x2 .

При x =1 и ∆x = 0,1 получаем ∆y = 0,43 , dy = 0,4, ∆y − dy = 0,03 . Следовательно, абсолютная погрешность | ∆y −dy |= 0,03, относительная погрешность

∆y −dy

= 0,03 ≈ 0,07 или 7%.

∆y

0,43

Пример 4.13. Найти приближенно sin 29 .

Решение. Так как ∆y = y(x +∆x) − y(x)

и ∆y ≈ dy , то y(x + ∆x) ≈ y(x) + dy .

3π

Пусть y =sin x , x =30

и ∆x = −1 . Тогда dy = cos xdx = cos30

−

= −

180

360

sin 29 =sin(30 −1 ) ≈ 1 −

3π

= 0,485.

360

		Задания для самостоятельного решения
4.15. Найти дифференциалы от функций:
1)	y = x2 +	1	;	2)	y =	1 + x	;	3)	y = ln x −cos 2x ;

		x2				x2 + x
4)	y = cos2 x −3x +1;			5)	y =ex arcsin 2x ;			6)	y =5x cos3x .

4.16. Найтидифференциалыизначениядифференциаловфункций y = f (x) :

1)y =sin3 2x . Найти df (x), df (π /8), df (π /8) dx=0,1 ;

2)y =ln(1+ x2 ) . Найти df (x), df (2), df (2) dx=0,01 .

4.17. Найти дифференциалы второго порядка:


1)	y = 2−x2 ;		2)	y = x2 −1 ;	3)	y =ln2 x + x ;
4)	y =sin2 (x +1) ;		5)	y −ln(cos x) ;	6)	y = 3 x +5 .
4.18.		Найти приращение и дифференциал функции y = x + 2 при x = 2
и ∆x = 0,01.		Вычислить абсолютную и относительную погрешности, которые
допускаются при замене приращения ее дифференциалом.
4.19. Найти приращение				∆y и дифференциал	dy функции y =arctge2 x

при x = 0 и ∆x = 0,02 . Вычислить абсолютную и относительную погрешности, которые допускаются при замене приращения ее дифференциалом.

4.20. Вычислить приближенно:
1)	3 27,01 ;	2)	lg10,03;		3)	arccos0,01;
4)	tg31°;	5)	′	;	6)	5	33 .
			sin 44°57

ТЕМА 3

ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ

Касательная

Уравнение касательной к графику дифференцируемой функции y = f (x)

в точке M0 (x0 , y0 ) , где y0 = y(x0 ) , имеет вид
y − y0 = y′(x0 )(x − x0 ) .			(4.6)
Углом между двумя кривыми y = f (x) и y = g(x) в точке их пересечения
называется угол между двумя касательными к их графикам в этой точке.
Уравнение нормали в точке M0 (x0 , y0 ) имеет вид
y − y0 = −	1	(x − x0 ), y′(x0 ) ≠ 0 .	(4.7)
	y′(x0 )

		47

Правило Лопиталя

Пусть функции f (x) и g(x) дифференцируемы в некоторой окрестности точки x0 , за исключением, быть может, самой точки x0 . Если

lim

x→x0

то

lim

x→x0

f (x)

g(x)

= lim g(x) = 0 или lim f (x) = lim g(x) = ∞,
x→x0		x→x0	x→x0
= lim	f ′(x)	,	(4.8)
= lim	g (x)	,	(4.8)
x→x0	g (x)
x→x0	′

при условии, что предел lim f ′(x) существует (правилоЛопиталя). Приэтомточка

x→x0 g′(x)

x0 можетбытькакконечной, такинесобственнойточкойравной +∞ или −∞.

Примеры решения задач

Пример 4.14. Найти уравнение касательной и нормали к кривой

y = x2 + x в точке x0 =1.

Решение. Так как y0 = y(x0 ) = 2 , y′(x) = 2x +1 и y′(1) =3 , то из (4.6) получаем уравнение касательной

y − 2 =3(x − 2) или y =3x − 4 ,

а из (4.7) – уравнение нормали

y −2 = −13 (x − 2) или y −2 = −13 x + 83 .

Пример 4.15. Найти наименьший угол между кривыми f (x) =5x −6 и g(x) = x2 .

Решение. Найдем точки пересечения графиков данных функций:

5x −6 = x2 x2 −5x + 6 = 0 .

Отсюда абсциссы точек пересечения x1 = 2 и x2 =3 . Тогда точки пересе-

чения имеют координаты M1(2;4) и M

′

2 (3;9) . Кроме того, f (x) =5 и g (x) = 2x ,

′

т.е. f (2) = f (3) =

и g (2)

4 , g (3) = 6 . По формуле (1.19) находим угол меж-

ду касательными:

tgϕ =

5 −4

= arctg

;

tgϕ

6 −5

= arctg

1 +5 4

+5 6 31

Пример 4.16. Найти lim ln x .

x→∞ x

Решение. Имеем неопределенность вида ∞ . Для ее раскрытия восполь-

∞

зуемся правилом Лопиталя (4.8):

ln x

∞

(ln x)′

= 0 .

lim

( x )′

= lim

x→∞

∞ x→∞

x→∞ x

2 x

x→∞

Пример 4.17. Найти lim ex −e−x . x→0 ln(1+ x)

Решение. Имеет место неопределенность вида 0 . Используем правило

⎩0

Лопиталя:

lim

ex −e−x

= lim

(ex −e−x )′

= lim

ex + e−x

= 2 .

ln(1 + x)

x→0

(ln(1 + x))′

x→0

1 + x

Пример 4.18. Найти lim

e2 x −1

x→0 sin2 3x

Решение. Раскрываем неопределенность вида 0 , используя правило

⎩0

Лопиталя:

lim

e2 x − x

= lim

(e2 x − x)′

= lim

2e2 x −1

sin2 3x

(sin2 3x)′

6sin 3xcos3x

x→0

Опять получили неопределенность вида

. Применяем повторно пра-

вило Лопиталя. При этом, т.к. lim6cos3x = 6 , то получаем

x→0

lim

2e2 x −1

= 1 lim

(2e2 x −1)′

1 lim

4e2 x

2 .

6sin 3xcos3x

(sin 3x)′

3cos3x

x→0

6 x→0

Пример 4.19. Найти lim

ln x .

x→+∞

Решение. Раскрывая неопределенность по правилу Лопиталя, получаем:

lim	ln x		∞	= lim	(ln x)′	= lim	1	= 0 .
lim	x	=		= lim	′	= lim	x	= 0 .
	x		∞		′		x
x→+∞				x→+∞		x→+∞
						1
Пример 4.20. Вычислить lim(ex + x) x .
				x→0			{		}
Решение. Имеем неопределенность вида							{		}	. Обозначим искомый пре-
Решение. Имеем неопределенность вида								1∞		. Обозначим искомый пре-

дел через A, т.е. A = lim(ex + x) x . Прологарифмируем обе части последнего ра-

x→0

венства и вычислим полученный предел:

ln A = ln lim(ex +x→0

	= lim	(
=	= lim
	x→0

Значит A = e2 .

1		1	= lim
x) x	= lim ln(ex + x) x		= lim
	x→0		x→0

ln(ex + x))′	= lim	ex +1			= 2 .
′
			x
x	x→0	e		+ x

ln(ex + x) = x

Задания для самостоятельного решения

4.21. Составить уравнение касательной и нормали к графику функции

y = f (x) в точке с абсциссой x0 .

f (x) = x3 ,

= 2;

f (x) =cos x, x =π / 4 ;

f (x) = ex ,

=1;

f (x) = x2 −2x +5,

= 0,5;

f (x) = x2 +1, x = 2 ;

f (x) =0,5sin2 (4x −π / 3), x

=π / 6 ;

f (x) = x−1, x = −1;

f (x) = xln x, x =e.

y = f (x)

4.22. Написать уравнения касательных к графику функции

точке с абсциссой x0 . Построить кривые и касательные:

f (x) =

+ 2, x = 2 ;

f (x) = 1 − x2 + 2, x = 0 ;

f (x) = x2 + x +1, x = 0 ;

f (x) = x2 − x, x = −1.

4.23. Под каким углом пересеваются кривые;

f (x) = x,

g(x) = 1 − x2 ;

2) f (x) = x3 − x,

g(x) =

;

f (x) = x,

g(x) = x−1 ;

4) f (x) = x,

g(x) = x2 ;

f (x) = x,

g(x) = 1 − x2 ;

6) f (x) =sin x,

g(x) = cos x .

4.24. Найти угол между касательными к графику функции

y = f (x)

точках с абсциссами x = −1 и x =1:

1) f (x) = x2 −1;	2) f (x) = x3 − x .
4.25. К кривой	y = x4 −2x2 +3x −1 провести касательные параллельные
прямой 3x − y +1 = 0 .

4.26.Найти уравнение горизонтальной касательной к графику функции

y = ex +e−x .

4.27.Найти координаты точки пересечения двух касательных, проведен-

ных к графику функции

y =

в точках с абсциссами x = −2 и x = 4 .

−3

4.28. Используя правило Лопиталя, вычислить пределы:

πx

lim e

3 x

− 4x −1

;

2) lim

;

sin2 5x

x→0

x→1

ln (1 − x)

lim

ln (x −1)

;

4) lim sin 3x ;

x→1

ctgπx

x→0

lim

−

e2 x −1

;

6) lim

;

−1

sin 3x

x→0

1 −cos5x

lim(1 +sin2 x)

tg2 x

;

8) lim

;

x→0

1 −cos3x

lim

(sin x)tgx ;

10) lim

x −sin x

;

x→0

11) lim

(sin(2x −1) tgπx); 12) lim tgx −sin x

;

x→1

x→0 x −sin x

				1
13)	lim (ln 2x)					;
13)	lim (ln 2x)				ln x	;
	x→+∞
14)	lim	ln2 x		;
14)	lim	3	x	;
	x→∞	3

15)	lim	ln cos(4x2 −3x)						;
15)	lim		sin 5x2					;
	x→0	xk	sin 5x2
17)	lim	xk	;
17)	lim	ax	;
	x→0	ax
19)	lim xln x ;
	x→0
21)	lim	1					;
21)	lim		−ctgx				;
	x→0	x
23)	lim(ln ctgx)tgx ;
	x→0

13) lim(cos x)ctg2 x ;

x→0

14)	lim	ln x			;
		ctgx
	x→0
16)	lim	(π− x)tg						x	;

	x→0		1		1		2
				−
18)	lim						;
						ln x
	x→0	x

20) lim ex + e−x − 2 ; x→0 1 −cos 2x

22) lim 1 sin x ;

x→+0 x

	2		+	1
24) lim x − x		ln 1	+	.
x→0				x

	Задания для индивидуальной работы № 9
Задание 9.1. Найти первые производные функций (см. табл. 9.1):
								Таблица 9.1
Номер
варианта
1	y = 3 (x + 2)2 + e−x				y =sin 2x ln x
	y =	32 x			y = arcsin 2cos(5 x+1)
2		cos(3x −1)
2	y = cos3x + ln			x	y = 27 x tg3x
	y =	x3			arccos x
	y =	sin(x −3)			y =3	5
3		sin(x −3)
	3 (2х−1)2 + tg(x2 +1)						x
	3 (2х−1)2 + tg(x2 +1)				y =sin 2x e3
		x2				2 x+1
4	y = cos x				y = arctg3
4	y = ctg2x +log2 x3				y = 3 x cos 2x
	y = sin 2x				y =3arcsin	x
5		ex
5	y =sin x2 +53x				y =ln(2x +3) (x +1)3
	y =	x +3			y = arccos tgx3
6		cos3x
6	y = log3 2x + tg(2x −1)				y = 32 x	3x −1
	y = sin x +1				y = 3 cos2 2x
7		x	x
			x		y = tg3x (x −1)2
	y = ctg 3 2x +33				y = tg3x (x −1)2
	y =	x2 + cos 4x			ln 5 2 x−3
	y =	32 x			y =3
8		32 x			y = ctg(2π − x) 5
8	y = 3 5x −1 + arctg(x − 2)				y = ctg(2π − x) 5					x
	y =	2x + x			y =sin arctg2−x3
9		cos 2x			y = arcsin 3x e−2 x
9	y = cos		x + ln(2 − x)		y = arcsin 3x e−2 x
	y =	3x +ln x			y =3arcctg 3 x2
10		4 x −1
10	y = tgx3 +3 x +1				y = log3 3 2 − x
	y =	(3 + x)2			y = arccosln		5	x	2
	y =	2x			y = arccosln			x
		2x
				52

					Продолжение табл. 9.1
11	y = 5 (1 − 2x)3 + tg2x				y =3x2 sin 2x
	y =	3x2 + x			y = log5 sin 22 x
12		cos 2x			y = arctgx x3
	y = log3		x + 2sin x
	y =	x +	x		y =arccosln(x2 + x)
13		sin 5x		1
	y = ctg(2x −1) +				y = tg3x 3−x2
	y = cos(3π − x)			2x
					y = earcsin x3
14			x3
	y = 3 (1 − 2х)2 + 2−2 х				y = arctg(x2 +1) 3x
	y =	32 x			y = cosln 2x
15		x − 2x2
	y = ctg2x + 2sin x				y = arctgx			2x
	y = ln(2x −1)				y =lnsin2 (x + 2)
16		3	x
	y =	3 + ecos x			y =sin2 x x2

		х5
	y =	3x +1			y = tg7sin 3x2
17		cos(2 − x)
	y =	sin x + 2−2 x					2
					y = tg3x x3
	y =	sin 3x +1			3	x	2
18		4x			y =5sin
	y = log9 sin x + 3			x2	y = ctgx2 (ln x +1)
		cos3x			y = sin arctg			x
19	y = x + ln x				y =cos3 x 23x
	y = 2 3 х2		+ e2 x
	y =	3x −1			y = arcctgsin(x2 −5)
20		sin 2x
	y =ln3 (2 + x) +32 x				y = ctg5x 2 x
	y = x2 +sin3				y =sin log2 x2
21		2x			y = tg3 x ln3x
	y =	2x2 − x + e3x
	y =	3x			y =log5 arcsin x2
		x2 +1
				53

Окончание табл. 9.1

2 x

y =sin

2x + 2x −1

y =10

y = sin (π −2x)

y = earcctg

y =log3 sin x + 22 x

y = sin x2 3

y =

3x2 +sin x

y =sin 7 x

y = cos(2x −1) +

y = 3 (2x −1)2 sin 3x

y = log5 2x

y =ctg2cos 3x

sin x

y = cos2 2x

y =54

х5 +sin 2x

y =

y = arcsin 3 2x2 − x

52 x

y =e2 x−1 sin x2

y = 5 2х2 − х + log32 x

y =

cos(3x +1)

y =5arcctg

23x

y =sin2 x + 2x2

y = tg (π − x) x5

y = ln x + x

y = log

sin

x2 − x

y =

+ esin x

y = 3 2x2 −1 sin x

3х−

y =

3x5

y = tg2 ln(x +1)

sin(1 − x)

y =sin x3 + 2−x

y = ctgx2 3

y =

3x2 +cos x

y =sin 2tgx2

ln x

y =

+cos ex

y = cos2 x 5x

2)5

(х+

y =

3x+1

y = ctg log3

sin 3x

Задание 9.2. Вычислить производную второго порядка (см. табл. 9.2):

Таблица 9.2

Номер		Номер
варианта		варианта
1	y =sin 2x + x2	16	y = 23х +ln x

Окончание табл. 9.2

2		y = е−2 x +						x +5					17	y = cos(2x −3) + 2x
3		y = 5 2х+3 + log2 x											18	y =10−х				+(х−3)2
4		y = tg3x +32 x−1											19	y =3х5 −sin3x
5		y = 3 х2				+ ln(2x +3)							20	y = cos5x −e−2 x+1
6		y = 2х2 −12sin x											21	y = 3 х + ln x2
7		y = 2sin (3π + x)+ x−3											22	y = 2 3		х−1 + ln 3x
8		y =10−			x	+ 7 х4							23	y = 2х+3 −5е−х
8		y =10−			5	+ 7 х4							23	y = 2х+3 −5е−х
9								π				3	24		1
		y = cos x −								+				y =	1		+32 x−1
		y = cos x −								+		4 x3		y =	2x3		+32 x−1
								4				4 x3			2x3
10			x										25	y = 3		х−3 + 2sin 5x
			x
		y = 7		+3log2 x
		y = 7	7	+3log2 x
11			2						x				26	y = arctg2x
		y = 3х−1 +3												y = arctg2x
		y = 3х−1 +3
12		y = e	−2 x			1							27	3		+sin (6π − x)
						+								y =
							3x2
							3x2								5х
13		y =3х2 −2х+1+ 23х											28	y = 3 (3х+1)2						+cos 2x
14		y = (5х−1)10 +е−5x											29	y = 2ln 3x +sin(2 − x)
15		y = log3 x +							1				30					π				x
15									1				30					π
														y = cos				3	−3x		+ e5
								2 x						y = cos					−3x		+ e5
								2 x
	Задание 9.3. Вычислить приближенно (см. табл. 9.3):																		Таблица 9.3
																			Таблица 9.3

	Номер											Номер		Номер
	варианта										варианта			варианта
	1	sin 290										11	cos610	21					tg610
	2	log2 2,02										12	3 8,02	22					cos 440
	3	cos 460										13	log3 2,98	23					log2 1,99
	4	tg290										14	sin 310	24					sin 440
	5	3,99										15	cos310	25					3 7,99
	6	sin 590										16	tg590	26					tg310
	7	log3 3,01										17	cos590	27					log3 2,99
	8	сtg310										18	tg460	28					cos 290
	9	sin 460										19	sin 610	29					log5 4,99
	10	tg440										20	4,02	30					3 7,98

Задание 9.4. Найти пределы, используя правило Лопиталя (табл. 9.4):

Таблица 9.4

Номер

варианта

lim sin x − x

lim

tg3x

2x −1

x→0

lim

ln(2 +3x )

lim

ln(1+ x)

x→∞ x2 + 2x +5

x→0

lim

x − tgx

lim

5х

−1

x→0

x→0 arc tgx

lim

2 x

−cos х

lim cos x −2

x→0

sin 3x

x→0

sin x − x

lim

arc tgx

lim

3х

x→0

x→∞ x

lim

ln(1 + x)

lim

1 −ex

sin x2 + x

x→0

lim

−1

lim

3х

−1

arcsin 2x

x2 + 7х

x→0

2 x

−1

lim

tgx

ех

x→0

x→∞

lim

arcsin x

1 −e

2 x

ех

x→∞

x→0

2 x

−1

lim

ln(1 + x)

x→0

x→∞ ln(1 + x2 )

lim

ln(1 + 2x)

lim

−1

x→∞

x→0 sin 3x

lim arcsin x

lim tg3x + x

x→0

sin x

lim

−cos x

lim

+3х−1

sin x

е2 х

x→0

x→∞

lim

tgx − x

х2

x→0

lim

−cos 2x

x→0

lim sin x + x

lim sin x − x

x→0

arc tgx

x→0

tg2x

ТЕМА 4

ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧЕСЛЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИИ

Признаки монотонности функции

Пусть функция f (x) определена и непрерывна на отрезке [a;b] и f (x) дифференцируема на интервале (a;b) . Тогда:

1)функция f (x) является неубывающей (невозрастающей) на [a;b] тогда и только тогда, когда f ′(x) ≥ 0 ( f ′(x) ≤ 0 ) для всех x из (a;b) ;

2)функция f (x) является убывающей (возрастающей) на [a;b] тогда и только тогда, когда f ′(x) > 0 ( f ′(x) < 0 ) для всех x из (a;b) .

Пусть функция f (x) определена и непрерывна на отрезке [a;b] и f (x) дифференцируема на интервале (a;b) . Функция f (x) является постоянной на (a;b) тогда и только тогда, когда f ′(x) = 0 всех x из (a;b) .

Экстремумы функции

Точка x0 называется точкой минимума (максимума) функции f (x) , если она определена в некоторой окрестности этой точки и для каждой точки x ≠ x0 этой окрестности f (x) ≥ f (x0 ) (соответственно f (x) ≤ f (x0 ) ). Значение функции f (x0 ) называется минимумом функции (соответственно максимумом функции).

Под экстремумом понимается либо минимум, либо максимум.

Точка x0 из области определения функции f (x) называется критической точкой, если функция f (x) дифференцируема в точке x0 и f ′(x) = 0 , или f (x) не дифференцируема в точке x0 .

Необходимое условие экстремума.

Если x0 – точка экстремума функции f (x) , то x0 – ее критическая точка.

Достаточные условия экстремума.

1.Пусть функция f (x) непрерывна в некоторой окрестности критической

точки x0 . Если при переходе через точку x0 производная функции меняет знак «+» на «–», то x0 – точка максимума; если при переходе через точку x0 производная функции меняет знак «–» на «+», то x0 – точка минимума; если при переходе через точку x0 производная не меняет знак, то в точке x0 экстремума нет.

2.Пусть в критической точке x0 функция f (x) дважды дифференцируе-

ма. Если при этом	f	′′
			(x) < 0 , то в точке x0 функция достигает максимума;
′′	x0		функция достигает минимума.
f (x) > 0 , то в точке
3. Пусть функция			f (x) задана параметрически:

x =u(t), y = v(t) ,
где функции u(t) и v(t) в некотором промежутке изменения аргумента t	имеют
′
производные первого и второго порядка, причем u (t) ≠ 0 . Пусть при t =t0
v′(t) = 0. Тогда если v′′(t0 ) <0 , то функция y = f (x) при x = x0 =u(t0 )	имеет

максимум; если v′′(t0 ) >0 , то функция y = f (x) при x = x0 =u(t0 ) имеет минимум; если v′′(t0 ) =0 , то вопрос о наличие экстремума остается открытым. Точки, в которых v′′(t) =0 требуют специального исследования.

Наибольшее и наименьшее значения функции

Наибольшее (наименьшее) значение функции, непрерывной на отрезке [a;b] , достигается или в критических точках функции или на концах отрезка.

Для того, чтобы найти наибольшее (наименьшее) значение функции на отрезке

[a;b]	надо вычислить значение функции во всех критических точках на отрезке
[a;b] ,	значения f (a) ,	f (b) на концах отрезка и выбрать наибольшее (наи-
меньшее) из полученных значений.
	Выпуклость и вогнутость функции.
		Точки перегиба
	Пусть функция	y = f (x) определена и дифференцируема на интервале
	′′			y = f (x)
(a;b) . Если f (x) < 0 в интервале (a;b) , то в этом интервале кривая
выпукла, т.е. ее график лежит ниже любой своей касательной; если f				′′
				(x) > 0 в
интервале (a;b) , то в этом интервале кривая			y = f (x) вогнута, т.е. ее график
лежит выше любой своей касательной.
	Если f ′′(x0 ) =0 или не существует, но		f ′(x0 ) существует и вторая произ-

водная f ′′(x) меняет знак при переходе через точку x0 , то точка (x0 , f (x0 )) яв-

ляется точкой перегиба кривой y = f (x) .

Асимптоты

Пусть M (x, y) − некоторая точка графика функции y = f (x) . Говорят, что

точка M удаляется в бесконечность по графику, если она движется по графику так, что или x →±∞, или y → ±∞.

Прямая линия называется асимптотой графика функции y = f (x) , если

расстояние от точки M , лежащей на кривой, до этой прямой стремится к нулю при движении точки M вдоль какой-нибудь ветви кривой в бесконечность.

Различают вертикальные, горизонтальные и наклонные асимптоты. Если

lim f (x) = ∞,

x→a

то	прямая	x = a	является	вертикальной	асимптотой	графика	функции
y = f (x) . Вертикальная асимптота параллельна оси Oy .
	Если
		lim	f (x) = c ,
		x→±∞
то	прямая	y = c	является	горизонтальной	асимптотой	графика	функции

y = f (x) (правая при x → +∞ и левая при x →−∞). Горизонтальная асимптота

параллельна оси Ox .

Если существуют пределы

k = lim	f (x)	и b = lim ( f (x) −kx) ,
	x
x→±∞		x→± ∞

то прямая y = kx +b – наклонная асимптота. Заметим, что горизонтальную асимптотуможнорассматриватькакчастныйслучайнаклоннойасимптотыпри k = 0 .

Общее исследование функции и построение ее графика

Общее исследование функции и построение ее графика можно проводить по следующей схеме:

1)найти область определения функции;

2)найти точки пересечения графика с осями координат;

3)исследовать функцию на четность, нечетность и периодичность;

4)исследовать функцию на непрерывность, найти точки разрыва и выяснить характер разрывов;

5)найти точки экстремума функции, вычислить экстремальные значения функции, установить интервалы монотонности функции;

6)найти точки перегиба графика функции, исследовать функцию на направление выпуклости;

7)найти асимптоты графика функции;

8)построить график функции.

График функции можно строить в следующей последовательности.

1)нанести точки пересечения с осями координат;

2)начертить все асимптоты;

3)нанести точки экстремума;

4)нанести точки перегиба;

5)при необходимости исследовать поведение функции при x →±∞;

6)начертить схематично кривую через нанесенные выше точки, учитывая поведение графика вблизи асимптот и при x →±∞;

7)полученный эскиз сравнить с результатами исследования: проверить промежутки монотонности, промежутки выпуклости и вогнутости и т. д.

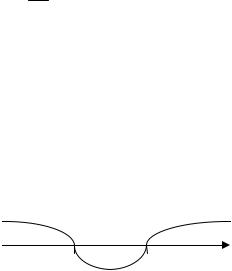
Примеры решения задач

Пример 4.21. Найти интервалы возрастания и убывания функции y = x + x42 .

Решение. Область определения функции x (−∞;0) (0;+∞) . Найдем

производную данной функции и точки, в которых производная равна нулю или не существует:

		′			8 x3 −8			3
	y						= 0 x −8 = 0 x = 2 .
			=1	− x3 = x3
			=1	− x3 = x3
Точка	x0 = 2			– критическая точка,					она разбивает область определения
								рассматриваемой функции на три интерва-
+						+		ла (рис. 4.1). В каждом из этих промежут-
0			−	2			х	ков	′
0			−	2			х	ков	производная y (x) сохраняет знак

(знак производной отмечен на рис. 4.1.). Рис. 4.1. Тогда данная функция возрастает на про-

межутках (−∞;0) и (2;+∞) и убывает на промежутке (0;2) . Пример 4.22. Найти экстремумы функции y = (x −1)2 (x +1)2 .

Решение. Функция определена и дифференцируема на всей числовой оси. Найдем ее критические точки. Так как

y′= 2(x −1)(x +1)2 + 2(x −1)2 (x +1) = 4x(x −1)(x +1) ,

то критические точки – x1 = 0, x2 =1, x3 = −1. Составим таблицу знаков производной на интервалах между критическими точками:

Интервалы

x < −1

−1 < x < 0

0 < x <1

x >1

′

−

Знак y (x)

Тогда x = −1

x =1

–

точки

локального

минимума

ymin = y(−1) = y(1) = 0 .

Точка x = 0

– точка

локального

максимума

ymax = y(0) =1.

Пример 4.23. Исследовать на экстремум функцию

y = 2x,

x > 0,

−3x − 4,

x ≤ 0.

Решение. Несложно заметить, что точка x = 0 – точка разрыва функции. Производная данной функции

2, x > 0, y = −3, x < 0

существует для всех x ≠ 0 . Тогда x = 0 – критическая точка. При переходе через точку x = 0 производная меняет знак «+» на «−», но максимума здесь нет, т.к. в этой точке нарушается непрерывность функции.

Пример 4.24. Найти наибольшее и наименьшее значение функции

y = x2 + 2x −3 − 32 ln x

на отрезке [0,5;1] .

Решение. Данная функция определена для x > 0 и имеет производную в каждой точке этого множества. Так как

y	′	= 2x + 2		3		4x2 + 4x −3		(2x −1)(2x +3)	,
			− 2x		=	2x	=	2x

то x1 = 0,5 и x2 = −1,5 – критические точки. При этом x2 [0,5; 1]. Находим зна-

чения исходной функции на концах заданного отрезка и в критической точке x1 = 0,5 .

y(0,5) = −1,75 +1,5ln 2 ,

y(1) = 0 .

Так как y(0,5) < 0 , то yнаим = у(0,5) = −1,75 +1,5ln 2 и yнаиб = у(0) = 0 .

Пример 4.25. Найти наименьшее значение функции y =1 +xx2 на проме-

жутке [−1;+∞) .

Решение. Для всех x > −1 данная функция дифференцируема и ее производная

y′ =

1 − x2

(

)

1 + x2

Критические точки x1 = −1 и x2 =1. Так как

y(−1) = −1

, y(1) = 1

и lim

= 0 ,

+ x2

x→∞1

то наименьшее значение функции на интервале [−1;+ ∞)

наим

= − 1

Пример 4.26. Найти промежутки

выпуклости

вогнутости функции

y =5x3 −3x2 + 4 .

Решение. Данная функция дифференцируема на всей числовой прямой. Найдем вторую производную:

y′=15x2 −6x, y′′=30x −6 .

Отсюда

y′′=0 x =0,2 . Так как

y′′< 0 ,

если

x < 0,2

и y′′> 0 ,

если

x > 0,2 , то исследуемая функция выпукла при x < 0,2

и вогнута при x > 0,2 .

При этом точка x = 0, 2 – точка перегиба.

Пример 4.27. Найти асимптоты кривых:

1) y =

;

2) y =

2x2

−1

Решение. 1) Кривая имеет вертикальную асимптоту x =1, так как

lim

= −∞;

lim

= +∞

x −

x −1

x→1−0

x→1+0

(точка x =1 является точкой разрыва второго рода).

Находим наклонные асимптоты:

k = lim

= lim

=1,

(x −1)x

x→∞ x

x→∞

b = lim( y − kx)

= lim

− x

= lim

=1.

x→∞

x −1

x→∞

x −1

Итак, прямая y = x +1 – наклонная асимптота.

2) Кривая имеет горизонтальную асимптоту y = 2 , так как

lim

2x2

= 2 .

x→∞ x2 +

Пример 4.28. Провести полное исследование функции

y =

и по-

x2 −1

строить ее график.

Решение.

1)Область определения функции x (−∞;−1) (−1;1) (1;+∞) .

2)Находим точки пересечения с осями координат. Если x = 0 , то y = 0 , т.е. график функции пересекает оси координат в точке (0;0) .

3)Так как


y(−x) =	(−x)3		= −	x3		= −y(x) ,
	(−x)2	−1		x2	−1

то функция нечетная и ее график симметричен относительно начала координат и достаточно исследовать функцию в промежутке [0;+∞) .

Функция не является периодической.

4) Исследуемая функция непрерывна в области допустимых значений. Точки x =1 и x = −1 являются точками разрыва. Исследуем характер точек разрыва.

lim

= −∞;

lim

= +∞;

x2 −1

−1

x→−1−0

x→−1+0

lim =

= −∞;

lim =

= +∞.

x2 −1

x→1−0

x→1+0

5) Исследуем функцию на монотонность. Находим точки экстремума:

y′ =	3x2	(x2	−1) − 2x x3				x2 (x2 −3)
					2	=					.
		(	x2 −	)	2	=	(	x2	)	2	.
			x2 −	1				x2	−1

Тогда y′= 0 x = 0 и x = ± 3 и в точках x = ±1 производная не существует. Разбиваем область определения функции на интервалы знакопостоянства производной: (−∞;− 3) (− 3;−1) (−1;0) (0;1) (1; 3) ( 3;+∞) . Опреде-

ляем знаки производной в этих интервалах, при этом, как было сказано выше, рассматриваем только промежуток [0;+∞) . Результаты для удобства записыва-

ем в таблицу

Интервалы

(0;1)

(1; 3)

(

3;+ ∞)

′

−

Знак y (x)

Монотонность y(x)

убывает

возрастает

Тогда точка x =

3 – точка минимума и ymin = y(

3 )=

≈ 2,6 .

6) Находим точки перегиба функции и интервалы выпуклости, вогнуто-

сти. Вторая производная исследуемой функции равна

−3)

′

2x(x

+3)

y′′ =

(x2 −1)3

(x2 −1)2

она обращается в ноль в точке x = 0 и в бесконечность при x = ±1. Определяем знак второй производной, результат записываем в таблицу:


Интервалы	(0;1)	(1;+ ∞)
′′	−	+
Знак y (x)	−	+
y(x)	выпукла	вогнута

7) Находим асимптоты графика.

Вертикальные асимптоты x = −1 и x =1 (см. п. 4). Наклонная асимптота:

k = lim

= lim

=1,

(x2 −1)x

x→∞ x

x→∞

b = lim( y − kx) = lim

− x

= lim

0 .

−1

x→∞

x→∞ x

Итак, прямая y = x является наклонной асимптотой.

8) Строим график исследуемой функции для

x [0;+∞) и отображаем

симметрично относительно начала координат (см. рис 4.2.).


Рис 4.2. График функции y =	x3		с асимптотами
Рис 4.2. График функции y =	x2	−1	с асимптотами
	x2	−1

Задания для самостоятельного решения

4.29. Найти промежутки возрастания и убывания функции:


1)	y = 2x2 −8x +15;				2)	y = x3 −8x2 ;
3)	y = x2ex ;				4)	y = xln x ;
5)	y =	x	− 3	x ;	6)	y =	x2	−1	;
		3					x2

y = x(3 x −1);

8) y = 2ex +3e−x ;

y = x3 −8x ;

10)

y = x +

;

−

11)

y = x2 ln x ;

12)

1 +

;

x2 −1

y = xe−2 x ;

13)

14)

y =5x ;

15)

y = ln2 x

;

16)

y = xx ;

17)

y = x2 −ln x2 ;

18)

y = (x +1)

x2 −1 .

4.30. Найти экстремумы функции:

y =

− x2 ;

2) y = ln x ;

y = xe−x ;

4) y = x2 (1 − x) ;

y = 2x3 +3x2 −12x +8;

6) y =(x −2)2 (x + 4) ;

y = x + 5 − x ;

8) y = x

2 +

;

y = x +

;

10)

y = (2x −1)e3x ;

11)

y = x3 −3x ;

12)

y =

+ x3 ;

13)

y =

;

14)

y = x(x −1)3 ;

−

15)

y = x

(1 − x) ;

16)

y =

;

x2 +1

17)

y = e−x2 ;

18)

y = ex .

4.31. Найти экстремум функции

−5t

− 20t +5,

(−2

<t < 2).

= 4t3 −3t2 −18t −5,

4.32. Найти максимумы и минимумы функций:

y =

;

2) 3 2x3 +3x2 −36x + 4 ;

x2 + 4

4) y = x2e−x .

y = xsin x ;

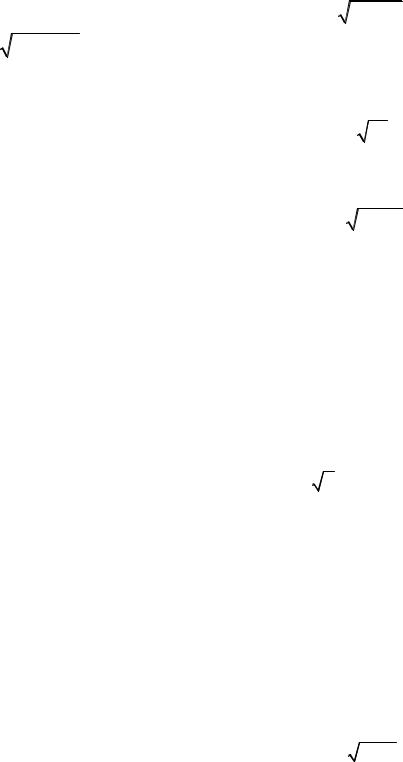
4.33. Найти наибольшее и наименьшее значения функции y = f (x) на за-

данном промежутке, если:
1) f (x) = x3 −3x2 +3x + 2, x [−2;2] ;	2) f (x) = x4 −8x2 −9, x [−1;3] ;

3)	f (x) =3x4 + 4x3 +1, x [−2;1];
5)	f (x) =	x	+ 3 , x [−5;−1] ;

	3		x
7)	f (x) =		x(10 − x), x [0;10] ;
9)	f (x) = x − 2ln x,				x [1;e];
11)	f (x) = ln x − x,				x (0;+∞) ;
13)	f (x) =		−x	,	x [−5;0) ;
			x2 +1

15)	f (x) = xln x − xln 5, x (1;5] ;

4)	f (x) =	x		+ 2 ,	x [1;6] ;

	8			x
6)	f (x) =			4		, x [−3;3];
				x2 +16
8)	f (x) = x3 − x,				x [0;4] ;
10)	f (x) =			x	,	x [−4;0];
				x2 + 4

12)	f (x) = −3 x2				− x, x [1;+∞) ;
14)	f (x) =			1	, x (−∞;+∞) ;
			1 + x2

16)	f (x) =			4 − x2		, [−1;1].

4.34. Найти интервалы выпуклости и вогнутости и точки перегиба сле-

дующих функций:

y = x +

1 ;

y = (1 + 2x2 )ex ;

y =3x3 −2x2 ;

y =

x2 + x

;

x2 +1

y =

x +1

;

y = x2 ln x ;

x2 + x +1

y =

;

y = 3 x(1 + x) ;

ln x

y = xex−1 ;

10)

y = x3 −3x.;

11)

y =

;

12)

y =

−9

;

13)

y =

;

14)

y = e−x2 ;

15)

y = x5 −5x3 +30x2 −4 ;

16)

y =

x −5

;

x + 4

17)

y = x2 −

;

18)

y = 4 − 3

x +3 ;

19) y =

;

20) y = x

x −8x + 4 .

x2 −

4.35. Найти асимптоты кривых:

y =

x2 +1

;

y =

;

− 2

−

y = xe−x ;

y = xln x ;

y =

5x2

;

y =

−1

−

4.36. Провести полное исследование функции и построить ее график:

y =

;

y =

−

;

−1

y =

;

y =

;

+ x)3

y =

x2 +1

;

y = x2 ln(x + 2) ;

x2 + x +

y = x3 −3x2 −9x ;

y =

x2 +1

;

x2 −1

y =

+ x

;

10)

y =

2x2 −9

;

x +

11)

y = 3

x2 −1;

12)

y =

(x +1)2

;

x −

2x2

13)

y =

;

14)

y =3x ;

x +1

15)	y = x −		x ;
17)	y =	x4		;
		x3 − 2

19)	y = (x +1)(x −2)2 ;
21)	y = x +e−x ;
23)	y = x −ln(x +1) ;

16)	y =	x3		;
16)	y =	x +1		;
		x +1
18)	y = 2 +				x3		;
18)	y = 2 +				x −	6	;
					x −	6
20)	y = 3 x2		−1;

=5(x −2)

22)y x2 ;

24)y = x + lnx .

Задания для индивидуальной работы № 10

Задание

10.1. Найти

наибольшее и наименьшее

значения

функции

y = f (x) на заданном промежутке (табл. 10.1).

Таблица 10.1

Номер

y = f (x)

промежуток

варианта

y =

+ 2−x

x [−1;2)

ln x

x [0,14;1)

y = e2 x−1 + 2e1−2 x +7x −3

y = 2 23x −9 22 x +12 2x

x [−1;1]

2x −log2 8x

y =log2

x 1/ 2;2

x [0;π]

y = cos

2 sin x

y =3x2 +2 x−1

x [−2;0]

x [1;4]

y = 2 xln x − xln 2

x [−2;4]

y =(x −3)ex+1

y =(x −3)2 ex

x [−1;4]

y = x2 ln x

x [1;e]

y = x +33 x

x [0;8]

y = xe−x

x [0;+∞)

y =

130 − x2

x [−7;8]

y = arctgx −

ln x

;

y =

x −1

x [−∞;4]

x +1

y = x

+ x −

x [2;+∞)

2 −ln x

x −1

x [0;1]

arctg x +1

y =

x [1;+∞)

1 + x

y = 3 (x2 −2x)2

x [0;3]

x2 +1

x [0;+∞)

y = x2 + x +1

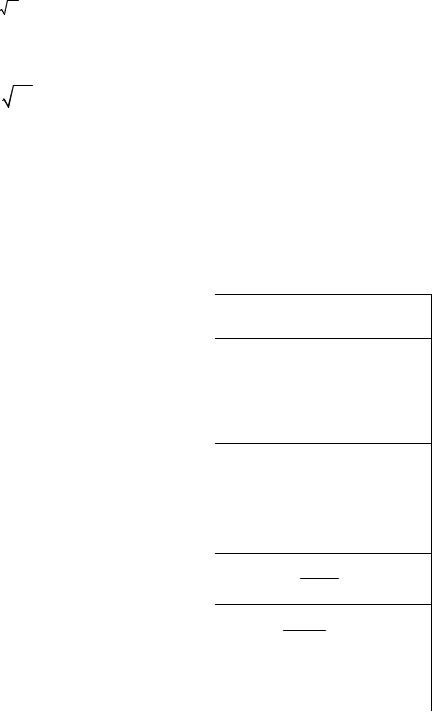
						Окончание табл. 10.1

21	y =(x −3)ex+1						x [−2;4]
22	y =3x2 +2 x−1						x [−2;0]
23		1					x [1;4]
	y = 2 x ln x − x ln 2						x [1;4]
	y = 2 x ln x − x ln 2
24	y =sin 2x − x						x [0;π]
25	y =			x −1			x (−∞;+ ∞)
	y =	x	2	−3x +	3		x (−∞;+ ∞)
		x	2	−3x +	3
26	y = 23 x2						x [−8;−1]
27		x2 + x +1					x (−∞;+ ∞)
	y =		x2 +3				x (−∞;+ ∞)
	y =		x2 +3
28	y = −3			x2 − x			x [1;+∞)
29	y =			x −1			x (−∞;+ ∞)
	y =	x	2	−3x +	3		x (−∞;+ ∞)
		x	2	−3x +	3
30	y =(x −3)2 ex						x [−1;4]

Задание 10.2. Провести полное исследование функции и построить ее график (табл. 10.2).

Номер

варианта

y = x

− 4

y =

1 −

y =

2( x−1)

2(x −1)

y =

−32

y =

1 − x2

y =

3−x

3 − x

y =

x + 2

x2 −1

Таблица 10.2

y =	e2(2+x)
y =	2(2 + x)
	2(2 + x)
y =		8x
y =	4	+ x2
	4	+ x2
y =		8x
y =	4	− x2
	4	− x2

y= 1 + 1 2

x y = ln x +x 2

y =1 −xx2

	y =	x2
	y =	(x −1)2
		(x −1)2

Окончание табл. 10.2

y =

12x

9 − x2

1 − x2

y =

2x −1

y =

12x

(x −1)2

9 + x2

y = x

y =

2−x

x2 −1

2 − x

y = x2 +

y = x2 −ln x2

y =

1 −x2x

y = x + x

y =

1 + x2

x −1

y =

(x −1)

y =

x +1

y = x2е−x

y = 4x2 +

<<< < Предыдущая 1 2 3 45 / 55

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
03.03.2016855.04 Кб213Lipinsky_Osnovy_intellektualnoy_sobstvennosti.doc
#
03.03.2016400.4 Кб8logika-konspekt_lekcij.pdf
#
03.03.20161.12 Mб10LOGIKA_UMP_KL_STR_113_DLYa_PDF.pdf
#
03.03.201632.02 Mб17lМирошникова О.С. Microsoft Office Word.docx
#
03.03.20164.5 Mб277Manual_Maxwell_render.pdf
#
03.03.20161.44 Mб17matem_2_chast.pdf
#
03.03.2016626.51 Кб26MathCad_Metoda_Lab.pdf
#
03.03.20168.37 Mб25Mathematics of Economics and Business.pdf
#
03.03.20162.72 Mб18Mat_modeli_OSA_konspekt_lektsiy.pdf
#
03.03.20161.01 Mб21Mat_modeli_OSA_lab_rab.pdf
#
03.03.20166.75 Mб14Metodicheskie_ukazania.doc