Шпора ОДМ( 2 модуль)

11

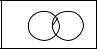
B-множество всех студентов в аудитории.

A-множество всех студентов мужского пола (горный факультет).

Если элементы множества A содержатся во множестве B, то записывается это следующим образом:

A B

и читается :"A содержится в B".

АКСИОМЫ ТЕОРИИ МНОЖЕСТВ

Существует 6 изначальных аксиом теории множеств:

1-Аксиома существования: "существует хотя бы одно множество".

Все аксиомы мы будем сопровождать диаграммами Эйлера.

2-Аксиома эквивалентности:

"если множество A и B состоят из одних и тех же элементов,

то они равны"

A=B

3-Аксиома объединения:

"Для двух произвольных множеств A и B существует такое множество

C, элементами которого является каждый элемент содержащийся хотя бы в одном из этих множеств".

I

A B

Аксиома обобщается на случай нескольких исходных множеств и звучит так: "Для произвольных множеств Ai существует множество C, элементами которого является каждый элемент, содержащийся хотя бы в одном из этих множеств Ai".

Аналитическое выражение для двух множеств:

C =A B

Для операции объединения справедливы свойства:

1) A A=A

14

Бинарная операция может быть записана следующим образом:

C=(A-B)+(B-A)=A B

ЗАКОНЫ ДЛЯ ПЕРЕСЕЧЕНИЯ И ОБЪЕДИНЕНИЯ .

Исходя из формулировки объединения и пересечения :

1.Закон коммутативности

A B = B A A B = B A

2.Закон ассоциативности

A (B C)=(A B) C A (B C)=(A B) C

3.Закон дистрибутивности

(A B) C=(A C) (B C)

Доказательство:

Рассмотрим выражение в левой части :

М=(A B) C

Если х М, то значит, что х С и одновременно А или В

Когда х А, х (А С), а когда х В х (В С)

Объединение этих выражений даѐт правую часть.

- (А В) С=(А С) (В С)

Доказательство:

Возьмем правую часть равенства. Согласно закону ассоциативности раскроем скобки и получим:

(А С) (В С)=А В С В А С С С=А В С (упростили используя закон поглощения ). Из записи закона ассоциативности и закона

дистрибутивности видно, что один закон можно получить из другого,

заменив знаки ― ‖ и ― ‖, следовательно, законы двойственны.

4. Закон поглощения

15

Если А содержится в В, то А B=В.

Согласно аксиоме объединения в результирующее множество входят элементы, принадлежащие хотябы одному А или В, а так как все А входят в В то справедливо:

А B=В

А А М=А

Исходя из определения операции пересечения ясно, что А М содержится в А.В итоге получаем А.

Следствие:

Если М=1, то А А=А

5.Свойство степени.

Если множество пересекается с самим собой, то из определения пересечения следует

А А=А

6.Законы де Моргана.

Эти законы позволяют выразить законы объединения и пересечения друг через друга с использованием операции дополнения :

а) А В= А В

Доказательство :

Обозначим через М: М=А В и М = А В . Если теперь объединение М и М даст

единичное множество, то закон будет доказан.

ММ = А В А В = А (В А ) (В В ). Используя определение дополнения получим :

ММ = А В А =1 В=1=I

б) А В= А В

Доказательство :

Обозначим через М: М=А В и М = А В . Если теперь объединение М и М даст единичное множество, то закон будет доказан.

16

М М = А В А В =( А А) (В А ) В = В А В =1 А =1=I

Законы де Моргана так же являются двойственными.

А В=АВ.

ВЫВОДЫ ПО РАЗДЕЛУ.

1.А А

2.Если А В и В А, то А=В

3.Если А В и В С, то А С

5.А I

6.А В =В А

7.А В =В А

8.А (В С)=(А В) С

9.А (В С)=(А В) С

10.А А = А

11.А (В С)=(А В) (А С)

12.А (В С)=(А В) (А С)

13.А = А

14.А I= I

15.А I = A

16.А A = A

17.А =

18.Если А В, то А В=В, А В=А

19.А А = I

20.A А =

21.=I

22.I =

23.А = A

24.Если А В, то В А

17

25.( А В ) = А В

26.( А В ) = А В

МИНИМИЗАЦИЯ ФУНКЦИОНАЛЬНОГО ПРЕДСТАВЛЕНИЯ

МНОЖЕСТВ.

Определим функцию от фрагментов, являющихся множествами. Функцией будем называть взаимооднозначное отображение элементов группы множеств Аi в

элементы множества С. Если каждому элементу С соответствует некоторый

элемент Аi, такую функцию называют всюду значимой С = f (Ai)

f – функция переводит элементы Ai во множество С.

Если пересечение множеств обозначать как функциональную операцию Р , то

Р (А,В) = АВ

На единичном множестве 1 заданы множества А,В,С. В этом случае с помощью известной операции над множествами переводим исходное множество в какое-

либо другое.

f (А,В,С) = АВС А В С A В C A В C АВ AС A С A В;

Записанное выражение назовем формулой. Определим сложность формулы, как

количество, содержащихся в ней исходных множеств. Для приведенного примера сложность =20. При аналазе формул первым вопросом является: «Можно ли

= В C В С = В C В C =1

f(А,В,С) = АС В С A ВС АВС АВ C A В C = АС В С A В АВ

=В АС В С;

Или :

18

F(А,В,С) = АС В С A ВС АВС АВ C A В C = АС В С ВС АВ C

A В C = АС В С ВС В C = С В C

Как видно из примеров минимизация одних и тех же функций может дать разные результаты при применении одних и тех же законов.

СТАНДАРТНЫЕ ФОРМЫ ПРЕДСТАВЛЕНИЙ ФОРМУЛ

МНОЖЕСТВ.

На 1 определении М1,М2,М3 совокупность Мi назовем порожд-ми множествами пространства и определим Мi по универсальной формуле:

Мi ; i =1;

Mi, i – первичный термом

n

Ki = M i i - конституентой

i 1

n - число порожденных множеств.

Перечислим все конституенты нашего примера:

К0 = М 1 М 2 М 3 К1 = М 1 М 2М3 К2 = М 1М2 М 3 К3 = М 1М2М3

К4 = М1 М 2 М 3 К5 = М1 М 2М3 К6 = М1М2 М 3 К3 = М1М2М3

Очевидно, что каждой приведенной коституенте может быть сопоставлено двоичное трехразрядное число, причем каждый разряд будет равен i первичного терма:

К0 = 000; К1 = 001; К2 = 010; К4 =011; К5 = 100; К6 = 110; К7 = 111.

Если учесть, что каждой конституенте длины П можно сопоставить n разр.

двоичное число, то общее количество конституент равно:

19

N = 2n

1)Выражения, заданные с помощью формул,могут быть упрощены.

2)Необходимые шаги для упрощения не всегда очевидны и сложность упрощения находится в прямой зависимости от числа аргументов в формуле.

3)Для упрощения выражения произв. вида и произв. количества аргументов

необходимо использовать математический аппарат минимизации функций подмножеств.

Пересечение двух различных конституент - пустое множество.

Пересечение двух конституент – есть пересечение всех первичных термов их составляющих, если конституенты не равны, то найдется хотя бы 1 разряд с несовпадающими первичными термами.

Обозначим этот разряд через i.

Mi i *Mi i*=

Объединение всех коституент, порожденных множествами Mi на универсальном множестве равно самому универсальному множеству:

j 0

С помощью конституент, образованных множествами Mi ,можно представить исходное универсальное множество.

1. Проиллюстрируем на графическом примере:

(универсальное множество I, внутри М1-квадрат, М2-треугольник, М3-круг).