
ступенях їх стехіометричних коефіцієнтів в рівнянні реакції.
Математичний вираз закону діючих мас називається кінетичним рівнянням. Для одностадійної гомогенної реакції, записаної у загальному виді:
аА + bВ сС + dD (1)
кінетичне рівняння має вигляд:
![]()
де k– константа швидкості реакції. Вона залежить від природи реагуючих речовин, температури, наявності каталізатора, але не залежить від концентрацій реагуючих речовин і часу перебігу реакції.
Для хімічних реакцій у розчинах в кінетичне рівняння не включають концентрацію розчинника, тому що вона практично не змінюється в ході реакції. З тієї ж причинидля гетерогенних реакцій у це рівняння не включають концентрації твердих і однокомпонентних (чистих, не утворюючих розчинів) рідких фаз, тому що вони залишаються постійними при перебігу реакції.
Приклад 2. Напишіть кінетичні рівняння наступних реакцій, вважаючи їх одностадійними:
а) 2Н2(г) + О2(г) 2Н2О(г)
б) С(гр.) + О2(г) СО2(г)
Розв’язання. а) Взаємодія між газами – це гомогенна реакція. Її кінетичне рівняння:
![]()
б) Реакція між графітом і киснем – це гетерогенна реакція, вона перебігає на поверхні графіту. Оскільки концентрації твердих речовин (у даній реакції – графіту) величини постійні, то вони включаються в вираз константи швидкості реакції, а в саме кінетичне рівняння не записуються:
![]()
Зміна тиску в системі, яка містить гази, приводить до відповідної зміни їх концентрацій. Вплив цих факторів на швидкість реакції однотипний.
Приклад 3. Розрахуйте, у скільки разів зросте швидкість реакції
2NO(г) + О2(г) 2NO(г)
при збільшенні тиску в системі в три рази.
Розв’язання. Позначимо концентрації вихідних речовин NOі О2 до зміни тиску відповідно с(NO) і с(О2). Залежність швидкості реакції від концентрацій реагуючих речовин до зміни тиску буде виражатися рівнянням:
![]()
При збільшенні тиску в системі у три рази концентрації усіх газів в системі теж зростуть в три рази і будуть дорівнювати 3с(NO) і 3с(О2). Залежність швидкості реакції від концентрацій реагуючих речовин після збільшення тиску в системі у три рази буде визначатися рівнянням:
![]()
Тоді:
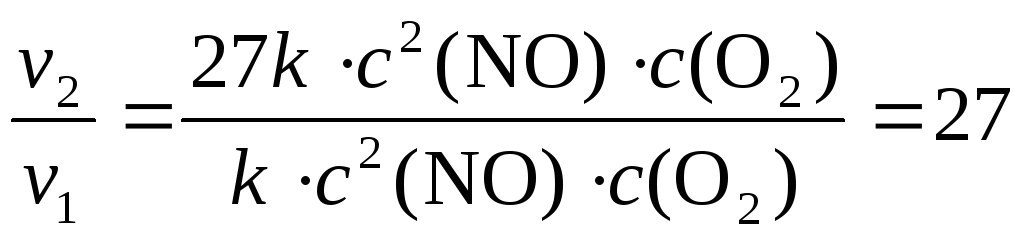
При збільшенні тиску в системі, де проходить ця реакція, в три рази швидкість реакції зростає в 27 разів.
Приклад 4. У реакційній посудині відбувається реакція:
А(г) + 2В(г) С(г)
Константа її швидкості при даній температурі дорівнює 0,4 л2/(моль2с), а початкові концентрації складали 0,3 моль/л і 0,5 моль/л для речовин А і В відповідно. Обчисліть швидкість цієї реакції в початковий момент часу, а також після того, як прореагує 0,1 моль/л речовини А.
Розв’язання. Запишемо під формулами речовин у рівнянні реакції їх молярні співвідношення, дані з умов задачі і невідомі величини, що необхідно обчислити:
А(г) + 2В(г) С(г)
1 моль 2 моль 1 моль
с0, моль/л 0,3 0,5 0
с, моль/л 0,1 x
с, моль/л у z
Розрахуємо, яка кількість речовини В прореагує з 0,1 моль речовини А:
![]()
Використовуючи співвідношення с = с - с0 , розрахуємо с для речовин А і В:
с(А) = у = с0 - с = 0,3 - 0,1= 0,2 моль/л,
с(В) = z = 0,5 – 0,2 = 0,3 моль/л.
Обчислимо початкову швидкість реакції:
v0=kc0(A)c02(В) = 0,4 л2/(моль2с)0,3 моль/л(0,5 моль/л)2= =310-2 моль/лс
і швидкість реакції в момент часу :
v=kc(A)c2(В) = 0,4 л2/(моль2с)0,2 моль/л(0,3 моль/л)2= = 7,2102моль/лс
швидкість реакції зменшилася приблизно у чотири рази за період часу .
Показник ступеня, з яким концентрація речовини входить у кінетичне рівняння, називається порядком реакції по даній речовині. Порядком реакції в цілому називають суму порядків реакції по всім реагуючим речовинам. Таким чином, кінетичне рівняння (1) відноситься до реакції порядку а по речовині А і порядку b по речовині В. Порядок реакції в цілому дорівнює (а+b).
Лише як випадок експериментально встановлений порядок реакції збігається зі стехиометричним коефіцієнтом в рівнянні хімічної реакції. У більшості випадків реакція перебігає не шляхом одностадійного прямого переходу частинок реагентів у частинки продуктів, а складається з багатьох простих (елементарних) стадій. Загальна швидкість і порядок реакції визначаються найбільш повільною елементарною стадією лімітуючою стадієюпроцесу.
Порядок реакції по даній речовині А зручно визначати за результатами серії дослідів, у якій змінюється концентрація саме цієї речовини при постійних концентраціях інших реагентів. Тоді кінетичне рівняння реакції (1) набуває вигляд:
v = kca(А)cb(В) = kca(А) (2)
де k = kcb(В) = const.
Після логарифмування рівняння (2) отримуємо залежність
lg v = lg k + аlg c(А) (3)
що у координатах lg v lg cА відображається прямою лінією з кутовим коефіцієнтом тангенсом кута нахилу прямої чисельно рівним порядку реакції a по речовині А.
Приклад 5. Визначте порядок реакції по кожному з реагуючих речовин і в цілому реакції окиснення хлориду заліза (II) пероксидом водню у водному розчині:
2FeCl2 + H2O2 = 2Fe(OH)Cl2
по наступних експериментальних даних (20оС):
|
Дослід |
1 |
2 |
3 |
4 |
5 |
|
сFeCl2, моль/л |
0,02 |
0,05 |
0,10 |
0,10 |
0,10 |
|
сH2O2, моль/л |
0,20 |
0,20 |
0,20 |
0,10 |
0,05 |
|
v, моль/(лс) |
0,32 |
0,81 |
1,58 |
0,80 |
0,40 |
Розв’язання. Для визначення порядку даної реакції по FeCl2 варто взяти результати серії дослідів 1, 2 і 3, у яких постійна концентрація H2O2 (0,20 моль/л), а для визначення порядку реакції по H2O2 – результати дослідів 3, 4 і 5 з постійною концентрацією FeCl2 0,10 моль/л. Обробка результатів вимірів має на меті підготувати дані для побудови графіка в координатах lg v lg cА. Для цього обчислюємо і записуємо в таблицю логарифми концентрацій і швидкостей реакції в зазначених дослідах:
|
|
Серія 1 |
| ||||
|
Дослід |
1 |
2 |
3 |
4 |
5 | |
|
|
Серія 2 | |||||
|
lg сFeCl2 |
-1,70 |
-1,30 |
-1,00 |
-1,00 |
-1,00 | |
|
lg сH2O2 |
-0,70 |
-0,70 |
-0,70 |
-1,00 |
-1,30 | |
|
lgv |
-0,49 |
-0,09 |
0,20 |
-0,10 |
-0,40 | |
Наносимо розраховані точки на графік (рис.2).
Для кожної з двох серій проводимо через нанесені точки прямі лінії так, щоб можливі (через експериментальні помилки) відхилення точок від них були мінімальні.
Для знаходження порядків розраховуємо тангенси кутів нахилу побудованих прямих. Зручно використовувати для цього відрізки, що відтинаються прямолінійними графіками на лініях, що паралельні осям координат. Щоб уникнути втрати точності, ці відрізки варто вибирати досить великими. На рис.2 для визначення tg узяті відрізки cd і ed, а tg fg і
hg. По координатах точок c, d, е, f, g, h визначаємо довжини відрізків, наприклад: cd = 0,21 – (-0,40) = 0,61; ed = (-1,00) – (-1,62) = 0,62.
О c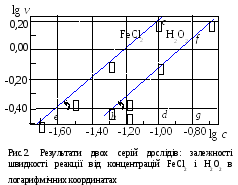
порядок реакції по FeCl2: а =tg = cd/ed= 0,61/0,62= 0,984;
порядок реакції по H2O2: b = tg = fg/hg = 0,50/0,50 = 1,00.
Відхилення знайденого значення порядку по хлориду заліза від одиниці обумовлено, мабуть, помилками вимірів.
Висновок. Досліджена реакція має перші порядки по обох реагентах: FeCl2 і H2O2. Порядок реакції в цілому дорівнює двом. Кінетичне рівняння дослідженої реакції має вигляд
v = k с(FeCl2) с(Н2O2).
Зверніть увагу, що експериментально знайдений порядок по FeCl2 не відповідає стехіометричному коефіцієнту в рівнянні реакції. Збіг порядку і стехіометричного коефіцієнта найчастіше виявляється випадковим.
По встановленому кінетичному рівнянню можна розрахувати константу швидкості, використовуючи дані кожного з дослідів. Наприклад, підставляючи в кінетичне рівняння результати досліду 5,
0,40 = k0,100,05
знаходимо константу швидкості дослідженої реакції при температурі дослідів
k = 0,40/(0,100,05) = 80 лмоль–1с–1.
Температура є одним із найсильніших чинників, що впливають на швидкість хімічної реакції. Майже завжди (а для елементарних реакцій беззастережно завжди) швидкість реакції зростає зі збільшенням температури.
Для реакцій, що перебігають при температурах, близких до звичайних, для приблизної оцінки впливу температури на швидкість можна користуватись правилом Вант-Гоффа:
З підвищенням температури на кожні 10 градусів швидкість реакції зростає в 2 - 4 рази.
За цим правилом швидкість є степінною функцією температури:
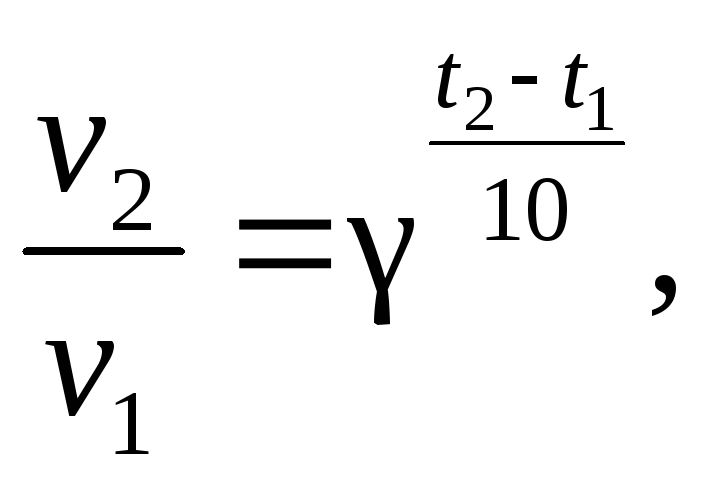
де v1 і v2 – швидкості реакцій при температурах t1 і t2, γ - температурний коефіцієнт, який показує, у скільки разів зростає швидкість у разі підвищення температури на 10 градусів.
Приклад 6. При підвищенні температури на 200С швидкість реакції збільшилась у 9 разів. Знайдіть температурний коефіцієнт реакції. Як зміниться швидкість цієї реакції при зміні температури від 40 до 700С і від 800С до 500С.
Розв’язання. Згідно з умовою задачі v2/v1 = 9, тоді за правилом Вант-Гоффа:
![]() або
9 = 2,
звідки
= 3.
або
9 = 2,
звідки
= 3.
При підвищенні температури від 40 до 100 0С швидкість реакції збільшується в 81 раз.
v2/v1
=
![]() = 33
= 81
= 33
= 81
Правило Вант-Гоффа є наближеним і дає розумні оцінки лише у неширокому інтервалі температур. Точну залежність, яка звязує константу швидкості реакції з температурою, дає рівняння Арреніуса:
![]() (4)
(4)
де k0 – предекспонційний множник (частотний фактор), ЕА – енергія активації, кДж/моль, R = 8,31 Дж/(Кмоль) – універсальна газова стала, Т – абсолютна температура, К. Символ ехр (експонент) вживається для більш зручного запису показової (експонентної) функції: exp z = ez.
Частотний фактор характеризує частоту коливань частинок реагуючих речовин уздовж ліній зв’язків, що розриваються, а також імовірність їх сприятливої для взаємодії орієнтації при зіткненні. Елементарний акт хімічної взаємодії протікає аж ніяк не при всякому зіткненні частинок. Необхідно, щоб вони мали деяку мінімальну надлишкову енергію, яку називають енергією активації ЕА. Вона необхідна для того, щоб частинки, що зіштовхуються, були здатні утворити активований комплекс (угруповання частинок у перехідному стані, коли розриваються старі й утворюються нові хімічні зв'язки). Множник ехр(-ЕА/RT), який називають фактором Больцмана, як раз і показує частку частинок, які мають необхідну додаткову енергію ЕА порівняно з середньою енергією теплового руху, що має порядок RT.
Лінеаризовану форму рівняння Арреніуса можна отримати логарифмуванням рівняння (4):
lg k = lg k0 – EA/(2,303RT) (5)
де 1/lgе = 2,303 модуль переходу від натуральних до десяткових логарифмів. У координатах lgk 1/T (ці координати називають арреніусівськими) залежність константи швидкості від температури зображується графічно прямою лінією. Відрізок, що відтинається цією прямою на вертикальній осі при (1/T) = 0, дорівнює lg k0, а нахил прямої пропорційний енергії активації:
tg = ЕА/(2,303RT) (6)
Приклад 7. Визначте енергію активації реакції, якщо при зростанні температури від 500 до 1000 К константа швидкості реакції збільшилась у 100 разів.
Розв’язання. Запишемо рівняння Арреніуса в логарифмічній формі (5) для першої і другої температури:
lg k1 = lg k0 – EA/(2,303RT1)
lg k2 = lg k0 – EA/(2,303RT2)
З метою отримання логарифму відношення k2/k1 віднімемо перше рівняння від другого:
lg k2 – lg k1 = (ЕА/2,303R)(1/T2 – 1/T1)
або
lg (k2/k1) = (ЕА/2,303R)(T1 – T2)/T1T2
Знаходимо величину ЕАіз цього виразу:
ЕА = lg (k2/k1) 2,303RT1T2/(T2 – T1)
ЕА = lg (100) 2,3038,315001000/(100 – 500) = 38200 Дж/моль.
За експериментальними даними енергію активації зручніше і наглядніше обчислювати графічним методом.
Приклад 8. Реакція між етилбромідом і лугом у водному розчині
C2H5Br + KOH C2H5OH + KBr
протікає по другому порядку. Визначіть енергію активації і предекспонційний множник по наступних експериментальних даних:
|
Дослід |
1 |
2 |
3 |
4 |
5 |
|
Т-ра, С |
25 |
30 |
35 |
40 |
45 |
|
k, л/(мольс) |
8,810-5 |
1,610-4 |
2,810-4 |
5,010-4 |
9,010-4 |
Розв’язання. Для побудови арреніусівського графіка обчислюємо значення lgk, абсолютної Т і зворотної температури 103/Т (для зручності, щоб не мати справи з
малими величинами з декількома нулями після коми, множимо 1/Т на 103).
|
Дослід |
1 |
2 |
3 |
4 |
5 |
|
Т, К |
298 |
303 |
308 |
313 |
318 |
|
103/Т, К-1 |
3,36 |
3,30 |
3,25 |
3,19 |
3,14 |
|
lgk |
-4,056 |
-3,796 |
-3,553 |
-3,301 |
-3,046 |
Наносимо на графік lg k 103/Т експериментальні точки (рис.3). Вони лежать на прямій лінії без значних відхилень – температурна залежність швидкості досліджуваної реакції добре описується рівнянням Арреніуса.
Визначаємо нахил прямої:
tg = (ab/bc) = 0,89/(0,19510-3K-1) = 4,56103 K
Енергію активації ЕА розраховуємо з формули (6) по знайденій величині нахилу:
EA = 2,303Rtg = 2,3038,31(-4560) 87300 Дж/моль = =87,3 кДж/моль
Визначення предекспонційного множника k0 графічно екстраполяцією прямої до перетинання з віссю при (1/T) = 0 у даному випадку незручно через значну далекість такої осі від поля графіка. Виконаємо чисельний розрахунок, використовуючи рівняння (5) і знайдене значення енергії активації. Так як всі експериментальні точки досить добре "лягли на пряму",можна скористатися даними кожного з
д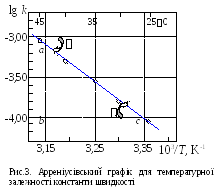 ослідів,
наприклад, п'ятого.
ослідів,
наприклад, п'ятого.
lg k0 = lg k + EA/(2,303RT)
lgk0=3,046 + 87300/(2,3038,31318) =3,046 + 14,348 ==11,302
звідки
k0= 1011,302= 2,001011(лмоль-1с-1)
Хімічні реакції бувають оборотні й необоротні. Необоротні реакції відбуваються доти, поки не витратиться повністю один із реагентів. Оборотні реакції можуть перебігати як у прямому, так і зворотному напрямках. Усі гомогенні реакції належать до оборотних. Такі реакції, як і усі процеси у природі, перебігають самодовільно доти реакційна система не досягне стану рівноваги. Хімічна рівновага має динамічний характер: у стані рівноваги швидкості прямої і зворотної реакцій однакові.
За умови рівноваги концентрації всіх речовин зв’язані між собою через вираз, що називають константою рівноваги. В разі зміни концентрації будь-якої з реагуючих речовин змінюються концентрації всіх інших. У результаті система переходить до нового стану рівноваги (кажуть, що рівновага зміщується), але співвідношення між рівноважними концентраціями, що виражається константою рівноваги, залишається незмінним.
Для оборотної реакції загального виду
аА + bВ сС + dD
константа рівноваги К записується так:
![]()
Рівноважні концентрації учасників реакції позначають формулою речовини у квадратних дужках: [А]. Це співвідношення називають законом діючих мас для хімічної рівноваги. На відміну від кінетичного рівняння, вираз для К залишається однаково вірним як для одностадійних, так і складних реакцій.
Константа рівноваги не залежить від концентрації, наявності або кількості каталізатора, а визначається природою учасників й температурою реакції.
Константа рівноваги є кількісною мірою стану рівноваги. При К 1 концентрації речовин у рівноважній реакційній суміші одного порядку величини (приблизно однакові), при К >> 1 в такій суміші переважають продукти (рівновага зміщена вправо), а при К << 1 переважають вихідні речовини (рівновага зміщена вліво). Якщо величина константи рівноваги дуже велика, К >>> 1, у рівноважній суміші концентрації вихідних реагентів можуть бути настільки малі, що їх не можна визначити за допомогою самих чутливих приладів. У такому випадку кажуть, що реакція перебігає як практично необоротна. Навпаки, при K <<< 1 вважають, що реакція практично не відбувається.
Приклад 9. Напишіть вирази для констант рівноваги реакцій:
а) Н2О(г)+ СО(г) СО2(г)+ Н2(г)
б) СО2(г)+ С(гр.) 2СО(г)
Розв’язання. Оборотна реакція (а) – гомогенна. Якщо учасниками реакції є гази, можемо в вираз константи рівноваги підставляти парціальні тиски замість концентрацій. Такий вираз позначають Кр на відміну від константи Кс, що виражають через концентрації. Отже:
![]() ,
,
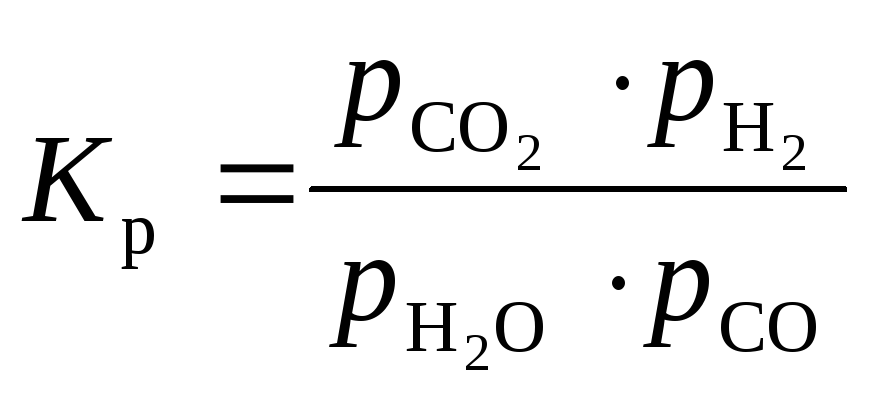
Гетерогенна реакція (б) є оборотньою за умови, що графіт узято у надлишку. У випадку гетерогенних реакцій концентрації твердих речовин не включають у вираз константи рівноваги, бо вони залишаються сталими при усяких зміщеннях рівноваги. Отже, для реакції (б):
![]() ,
,

Приклад 10. При деякій температурі у посудині ємкістю 1л змішали 5 моль N2 і 8 моль Н2. До моменту досягнення рівноваги реакції прореагувало 2 моль N2. Обчисліть константу рівноваги реакції при цій температурі.
Розв’язання. Позначимо початкові концентрації через с0, рівноважні ср, а зміну концетрації по ходу досягнення рівноваги як с = ср – с0. Запишемо рядками під формулами учасників цієї гомогенної оборотної реакції молярні кількості речовин, дані з умов задачі і невідомі величини, що необхідно обчислити:
N2 + 3Н2 2NH3
1моль 3 моль 2 моль
с0, моль/л 5 8 0
с, моль/л -2 - х у
ср, моль/л 3 8-х у
Зверніть увагу, що згідно з умовою задачі початкова концентрація продукту реакції – аміаку – дорівнює нулю. Для вихідних речовин с < 0 (їх концентрація зменшується), а для продуктів – с > 0 (концентрація зростає).
Визначаємо, скільки молей водню прореагує з 2 моль азоту до досягнення рівноваги реакції і скільки молей аміаку утвориться до цього моменту. Згідно із стехіометрією:
x = (3:1) 2 = 6 моль
у = (2:1) 2 = 4 моль.
Далі знайдемо рівноважні концентрації усіх учасників реакції N2, H2 і NH3 (враховуємо, що вони співпадають з числами молей, тому що об'єм дорівнює одному літру):
ср(N2) = c0 + c = 5 + (-2) = 3 моль/л;
ср(Н2) = с0 + с = 8 + (-6) = 2 моль/л;
ср(NН3) = c0 + c = 0 + 4 = 4 моль/л.
Підставляємо розраховані чисельні значення рівноважних концентрацій у вираз константи рівноваги і розраховуємо її величину:
 л2/моль2
л2/моль2
Рівноважний стан – найбільш стійкий стан системи за даних умов. Самодовільний вихід системи з цього стану неможливий. Змінюючи умови, можна перевести систему з одного рівноважного стану в інший, що буде найбільш стійким за нових умов. Такий перехід називається зміщенням рівноваги. Після досягнення рівноваги концентрації учасників реакції, як і інші параметри стану системи, самодовільно не змінюються.
Напрям зміщення рівноваги можна визначити за принципом Ле Шательє:
Якщо на систему, що перебуває у стані рівноваги, впливати ззовні, то рівновага зміщується у бік тієї реакції, що послаблює цей вплив.
Згідно з принципом Ле Шательє:
нагрівання зміщує рівновагу у бік ендотермічної, а охолодження – екзотермічної реакції;
підвищення тиску зумовлює зміщення рівноваги у бік реакції, що створює меншу кількість газів (а значить, сприяє зменшенню тиску в системі), а зниження тиску – у протилежний бік;
введення в систему додаткової кількості будь-якого з реагентів викликає зміщення рівноваги у тому напрямку, в якому його концентрація зменшується. Так, введення в систему вихідних речовин зміщує рівновагу в бік продуктів реакції ("праворуч"), а збільшення концентрації продуктів – в бік утворення вихідних речовин ("ліворуч").
Приклад 11. Визначте напрямок зміщення рівноваги реакції: 2SO2(г) + О2(г) 2SO3(г); Н0298 = -197,8 кДж при: а) підвищенні тиску; б) підвищенні температури; в) введенні в систему додаткової кількості SO3.
Розв’язання. а) Оскільки реагують три молекули газів (дві молекули SO2 і одна молекула О2), а одержують дві (дві молекули SO3), то підвищення тиску зміщує рівновагу праворуч. При підвищенні тиску з більшою швидкістю буде перебігати пряма реакція, в ході якої тиск падає. Саме пряма реакція послаблює зовнішній вплив на рівноважну систему.
б) За знаком зміни ентальпії цієї оборотної реакції визначаємо, що пряма реакція екзотермічна (Н 0), а зворотна – ендотермічна (Н 0). З ростом температури з більшою швидкістю перебігає зворотна реакція, яка супроводжується поглинанням теплоти. Саме ця реакція послаблює зовнішній вплив на систему. Рівновага зміщується у бік цієї реакції, ліворуч.
в) При підвищенні концентрації SO3 з більшою швидкістю перебігає зворотна реакція (для неї SO3 – вихідна речовина, концентрація якої в ході реакції зменшується). Рівновага зміщується ліворуч.
ДОМАШНЄ ЗАВДАННЯ
1. Для реакції 2NO(г)+O2(г)2NO2(г) запишіть кінетичне рівняння і визначте, як зміниться швидкість реакції, якщо:
а) збільшити концентрацію NO у 3 рази; б) збільшити тиск у системі в 3 рази; в) збільшити обєм системи в 2 рази.
Відповідь: а) зросте у 9 разів; б) зросте в 27 разів; в) зменшиться у 8 разів.
2. Розрахуйте, у скільки разів зміниться швидкість реакції окиснення вуглецю до вуглекислого газу, якщо тиск кисню збільшити в 4 рази? Відповідь: збільшиться у 4 рази.
3. Обчисліть, у скільки разів збільшиться швидкість деякої хімічної реакції при підвищенні температури на 1000С, якщо її температурний коефіцієнт дорівнює двом.
Відповідь: в 1024 рази.
4. Відомо, що деяка хімічна реакція при 1000С перебігає за 30 хвилин. Температурний коефіцієнт її дорівнює двом. Розрахуйте час протікання цієї реакції при 50 0С і при 150 0С.
Відповідь: 16 годин; 0,94 хвилини.
5.Через деякий час після початку реакції N2(г)+ 3Н2(г)2NH3(г) концентрації речовин складали: с(N2) = 0,03 моль/л; с(Н2) = =0,01 моль/л; с(NH3) = 0,008 моль/л. Розрахуйте вихідні концентрації азоту і водню та як змінилася швидкість реакції за цей проміжок часу.
Відповідь: с0(N2) = 0,034 моль/л; с0(Н2) = 0,022 моль/л, зменшилася в 12 разів.
6. Початкові концентрації реагентів реакції 2CO(г) + O2(г) 2СO2(г) складають: с0(СО)= 0,04 моль/л, с0(О2) = 0,06 моль/л. Константа швидкості дорівнює 0,4 л2/моль2с. Розрахуйте початкову швидкість реакції і швидкість реакції через деякий час, коли концентрація СО зменшиться на 0,02 моль/л.
Відповідь: 3,8410-5 моль/(лс); 810-6 моль/(лс).
7. Напишіть вираз константи хімічної рівноваги для процесу дисоціації вуглекислого газу згідно з рівнянням: 2СО2(г) 2СО(г)+О2(г), можливого в умовах вибуху у шахті. Як впливають зростання тиску і температури на цю рівновагу?
8. Для оборотної реакції
FeO(к)+СО(г) Fe(к)+СО2(г); Н0298 = -18,2 кДж
напишіть вираз константи рівноваги і вкажіть напрямок зміщення рівноваги при: а) збільшенні температури; б) зменшенні тиску; в) збільшенні концентрації СО.
9. При деякій температурі рівновага в системі 2NO2(г)2NO(г)+О2(г) встановилася при наступних концентраціях: ср( NO2 ) =0,04 моль/л, ср(NO) = 0,012 моль/л. У вихідній реакційній суміші знаходився тільки оксид азоту (IV). Розрахуйте рівноважну концентрацію кисню, константу рівноваги реакції і вихідну концентрацію NO2.
Відповідь: 610-3моль/л; 5,410-4; 5,210-2моль/л.
10. Обчисліть константу рівноваги реакції N2O4(г) 2NO2(г), якщо відомо, що початкова концентрація N2O4 дорівнювала 0,06 моль/л, до встановлення рівноваги продисоцюювало 30% цієї речовини, а NO2 в вихідній реакційній суміші був відсутній. Відповідь: 3,0910-2 моль/л.
9. Концентрація розчинів. Властивості розчинів неелектролітів
Мета вивчення теми:
- визначати молярну cм, моляльну cm концентрації, молярну концентрацію еквівалентів cн, масову частку в процентах (процентну концентрацію) ω(Х), мольну частку розчиненої речовини і розчинника x(X);
- застосовувати закон Рауля для визначення зниження тиску насиченої пари розчинника, температур кипіння і замерзання розчинів, знаходження молекулярних мас розчинених речовин.
В різноманітних наукових і технічних розрахунках застосовують різні способи вираження концентрації розчинів.
Розчин завжди складається, як мінімум, із двох компонентів: розчиненої речовини (Х2) і розчинника (Х1). Концентрація розчину визначається кількістю розчиненої речовини (у грамах, молях, молярних масах еквівалентів) у визначеній кількості розчину або розчинника.
Введемо такі позначення: m1- маса розчинника (г), M(x1)- молярна маса розчинника (г/моль), m2 – маса розчиненої речовини (г), M(x2) - молярна маса розчиненої речовини (г/моль), Мекв(x2)- молярна маса еквівалентів розчиненої речовини (г/моль), m- маса розчину (г), V- обєм розчину (л).
Приклад 1. Визначити масову частку в процентах розчиненої речовини у розчині, отриманому змішенням 300 г 25%-го і 400 г 40%-го (по масі) розчинів цієї речовини.
Розв’язання. Масова частка визначається формулою
ω%(Х)= (m2 /m) 100%
а) Знаходимо масу розчину, що утворився при змішуванні:
m = m1 + m2 = 300 + 400 = 700 г
б) Маса розчиненої речовини в 25%-му розчині (І):
m2 (I) = 3000,25 =75 г
і в 40%-му розчині (II):
m2 (II) = 4000,4 =160 г.
в) Визначаємо загальну масу розчиненої речовини в отриманому розчині:
m2 = m2 (I) + m2 (II) =75 + 160 = 235 г
і розраховуємо її масову частку в розчині:
ω%(Х) = (235/700)100 = 33,6%.
Приклад 2. Густина 15%-го розчину H2SO4 дорівнює 1,105 г/мл. Обчислити: а) молярну концентрацію еквівалентів; б) молярність; в) моляльність розчину.
Розв’язання. Будемо вести розрахунки на m=100 г розчину, що містять m2 = 15 г розчиненої речовини (H2 SO4) і m1 =85 г розчинника (H2O). Обєм V цього розчину дорівнює: V = m/ ρ = =100/1,105 = 90,5 мл або0,0905 л.
а) Молярну концентрацію еквівалентів (або нормальну концентрацію) cн визначають по формулі:
cн = nекв(X2)/V = m2/(Mекв(X2)V),
де nекв(X2) - число моль еквівалентів розчиненої речовини.
Визначаємо молярну масу еквівалентів сірчаної кислоти:
Mекв(H2SO4) = ƒ·M(H2SO4) = 1/2·98 = 49 г/моль,
де ƒ – фактор еквівалентності (найменший) сірчаної кислоти.
Підставляємо знайдені величини у формулу для cн і знаходимо: cн=15/(49·0,0905) = 3,38 моль/л.
б) Молярну концентрацію обчислюємо за формулою:
cм=m2/ (M(X2)·V) =15/(98·0,0905) =1,69 моль/л.
в) Моляльну концентрацію знаходимо за формулою:
cm= m2·1000/( M(X2) · m1) =15·1000/(98·85) = 1,8 моль/кг.
При розгляді властивостей неелектролітів необхідно пам'ятати, що неелектроліти - це речовини, що не проводять електричний струм, тому що при розчиненні молекули неелектролітів не розпадаються на іони.
Тиск насиченої пари над розчином завжди нижчий, ніж над чистим розчинником. Кількісна залежність зниження тиску насиченої пари над розчином неелектроліту від концентрації розчину описується законом Рауля і виражається формулою:
ΔР =Р0 х(Х2),
де Р0 – тиск насиченої пари над чистим розчинником; Р- тиск насиченої пари над розчином; ΔР= (Р0 – Р) - зниження тиску насиченої пари над розчином; х(Х2)- мольна частка розчиненої речовини, що визначається за формулою:
х(Х2) = n(Х2)/ (n(Х1) + n(Х2)),
де n(Х2) і n(Х1)- кількість моль розчиненої речовини і розчинника, відповідно.
Приклад 3.Чому дорівнює тиск насиченої пари води над 10%-мрозчином карбаміду CO(NH2)2при 100ºС?
Розв’язання. При 100ºС тиск насиченої пари над водою Р0 дорівнює 760 мм.рт.ст., або 101,3 кПа. З умови задачі випливає, що маса карбаміду на кожні 100 г розчину складає 10 г, а маса води - 90 г. Визначаємо мольну частку карбаміду у цьому розчині:
х(Х2)=n(Х2)/(n(Х1)+n(Х2)) = m2/M(Х2)/(m1/M(Х1) +m2/M(Х2)) =
= (10/60)/(90/18+10/60) = 0,167/(5+0,167) = 0,032.
Розраховуємо зниження тиску насиченої пари води над розчином згідно із законом Рауля:
ΔР= Р0·х(Х2)=101,3·0,032=3,24 кПа.
Знаходимо тиск насиченої пари над розчином:
Р = Р0 – ΔР = 101,3 – 3,24 = 98,06 кПа.
При визначенні температур кипіння і замерзання розчинів неелектролітів треба пам'ятати, що розчини киплять при більш високих, а замерзають при більш низьких температурах, ніж чисті розчинники. Як випливає з закону Рауля, підвищення температури кипіння ΔТк і зниження температури замерзання ΔТз розчину неелектроліту прямо пропорційні моляльній концентрації розчину:
ΔТк = Ке · cm, ΔТз = Кк · cm,
де ΔТк = Тк(розчину) – Тк(розчинника) = Тк – Тко;
ΔТз= Тз(розчинника) – Тз(розчину) = Тзо – Тз.
(В наших позначках температура з верхнім "ноликом" відноситься до чистого розчинника, а без нього – до розчину).
Ебуліоскопічна Ке і кріоскопічна Кк константи рівні, відповідно, підвищенню температури кипіння і зниженню
температури замерзання одномоляльного розчину (cm = 1).
Приклад 4. У радіатор автомобіля залили 9 л води і додали2 лметилового спирту (ρ= 0,8 г/мл).При якій щонайнижчій температурі можна після цього залишати автомобіль на відкритому повітрі, не побоюючись, що вода у радіаторі замерзне?
Розв’язання. Відповідно до закону Рауля:
ΔТз = Кк · cm = Кк · n(Х2)· 1000 / m1= Кк · m2·1000/ М(Х2)· m1.
Для води Кк = 1,86 Ккг/моль. Маса метилового спирту дорівнює: m2=V·ρ=2000·0,8=1600г, а молярна маса: М2(CH3OH) =32 г/моль.
Маса води m1 у розчині дорівнює: m1 = 9000·1,0 = 9000 г.
Підставляємо дані у формулу і визначаємо зниження температури замерзання розчину:
ΔТз = 1,86·1600·1000/(32·9000) = 10,3 ºС.
Знаходимо температуру замерзання даного розчину:
Тз = Тзо – Δ Тз= 0 – 10,3 = -10,3ºС.
Це щонайнижча температура, при якій ще можна залишати автомобіль на морозі.
Приклад 5. Скільки сахарози С12Н22О11 треба розчинити в 100 г води, щоб: а) знизити температуру кристалізації на 1 градус? б) підвищити температуру кипіння на один градус?
Розв’язання.По закону Рауля:
Тз = Кксm = Кк · m2·1000/ М(Х2)· m1
Визначаємо звідси масу сахарози m2, необхідну для зниження температури кристалізації на 10С:
m2 = Тз· M(Х2)· m1/( Кк·1000)
M(Х2) = М(С12Н22О11) = 324 г/моль
m2 = 1·342·100/(1,86·1000) = 18,4 г.
Аналогічно визначаємо масу сахарози, необхідну для підвищення температури кипіння на 10С:
m2 = Тк·M(Х2)·m1/(Ке·1000)
m2 =1·324·100/(0,52·1000) = 65,8 г
Дуже часто по підвищенню температури кипіння і зниженню температури замерзання розчину визначають експериментально молярну масу розчиненої речовини.
а) Ебуліоскопічний метод визначення молярної маси:
M(Х2 ) =Ке·m2·1000/(Тк·m1);
б) Кріоскопічний метод визначення:
M(Х2) = Кк·m2·1000/( Тз·m1).
Приклад 6. Водно-спиртовий розчин, що містить 15% спирту,кристалізується при -10,26ºС.Знайти молярну масу спирту.
Розв’язання. Так як мова йде про кристалізацію розчину, то застосуємо кріоскопічний метод для визначення молярної маси спирту.За умовами:m2(спирт)= 15 г,m1(вода) = 85 г.
ΔТз= 0 – (-10,26) = 10,26ºС. КонстантаКк(Н2О) = 1,86.
Знаходимо молярну масу спирту:
M(Х2) =Кк·m2·1000/(Тз·m1) = 1,86·15·1000/(10,26·85)=32г/моль.
ДОМАШНЄ ЗАВДАННЯ
1. Який обєм 14%-го (по масі) розчинуHCl(ρ=1,07 г/мл)буде потрібен для повного розчинення: а) 24,3 г Mg? б) 27,0 гAl?
Відповідь: а) 487,3 мл; б) 731,0 мл.
2. Для нейтралізації 20 мл 0,1 н розчину кислоти треба 8 мл розчинуNaOH.Скільки грамів NaOHмістить 1 лцього розчину? Відповідь:10 г.
3. Розрахуйте моляльну концентрацію хлориду магнію в підземних водах, якщо відомо, що його процентна концентрація складає 1%. Відповідь: 0,1 моль/кг.
4. Є розчини хлориду алюмінію і хлориду магнію у воді. Молярна концентрація у них однакова. У якому випадку моляльність розчину буде більша? Поясніть, застосувавши найпростіший розрахунок.
Відповідь: cm(AlCl3) буде більша.
5. Розчин складається з 50 гметилового спирту (CН3ОН)і50 г етилового (C2Н5ОН).Як варто назвати цей розчин: розчином етилового спирту в метиловому або метилового в етиловому? Відповідь перевірте розрахунком мольних часток цих речовин.
Відповідь:x(CН3ОН) = 0,59;x(C2Н5ОН) = 0,41.
6. При 315 Ктиск насиченої пари над водою дорівнює 8,2 кПа.Як понизиться тиск пари при зазначеній температурі, якщо в 540 гводи розчинити 36 г глюкози С6Н12О6?
Відповідь: на 54 Па.
7. При 293 К тиск насиченої пари над водою дорівнює
2,34 кПа. Скільки грамів гліцерину C3Н5(ОН)3треба розчинити в 180 гводи, щоб понизити тиск пари на 133,3 Па?
Відповідь:55,6 г.
8.Обчисліть масову частку водного розчину глюкози С6Н12О6,знаючи, що цей розчин кипить при 100,26ºС.
Відповідь : ω%(С6Н12О6) = 8,3%
9.Розчин, що містить 25,65 гдеякого неелектроліту в 300 г Н2О,кристалізується при -0,465ºС.Обчисліть молярну масу розчиненої речовини. Відповідь:342 г/моль.
10. Обчисліть температуру кипіння 15%-говодного розчину пропілового спирту C3Н7ОН. Відповідь: 101,5ºС.
