Шпора ОДМ( 2 модуль)

21

Следовательно, Mi можно представить в виде:

2 ^( n 1)-1

Мi = к l l 0

kl -конституенты, содержащие Mi.

ТЕОРЕМА.

Любая функция от порождающих множеств представима в виде объединения конституент.

Из аксиоматичного построения следует, что все операции представимы через операции объединения и отрицания.

Следовательно, достаточно доказать ,что объединение порождающих множеств представимо через объединение конституент, а так же ,что отрицание объединения конституент ,так же представимо через объединение множеств.

Для доказательства рассмотрим объединение произвольно образованных множеств Mi и Мк.

Согласно утверждению (Mi Мк) ,записывающихся в виде:

при этом М – различно, так как различно число совпадающих конституент в представлениях множеств Mi и Мк.

Остается доказать, что дополнения к объединению конституент в свою очередь есть объединение конституент .

Так как универсальльное множество является объединением всех конституент,

ясно, что если взять объединение некоторых из них, то оставшиеся конституенты будут дополнительными к исходному объединению.

Рассмотрим пример:

Функция от множеств А,В,С

22

f(A,В,С) = А(В ((С А)\В)) = А(В ((С A С A )\В)) = А(В (С A C А) B )

= А(В С A В С А В ) = АВ С А В = А В С АВС АВ С

Из пересечения АВ получена АВС A В С. Ясно ,чтобы получит трех-

разрядную конституенту, необходимо до термов АВ добавить С, а так как произв-но множество М:

М(С С ) = МС М С АВ = АВС АВ С то просто получим из АВ трехразрядную конституенту.

Итак , любая функция от порождающих множеств , может быть представлена в виде объединения коституент и оно называется совершенной норм.Кантора

(СНФК).

Если в представлении функции участвовали конституенты меньшей длины,

то оно называется норм. формой Кантора (НФК).

Для получения РФК нужно минимизании СНФК любым (аналитическим,

графическим, графо-аналитическим способом).

Назовем интервалами универсального пространства ранга n все коституенты

Если рассмотреть предыдущий пример, то можно заметить ,что f(А,В,С): f (A,В,С) = АВ А В С

где, АВ покрывает АВС и АВ С , а втор. совпадает с А В С .

ГРАФИЧЕСКАЯ МИНИМИЗАЦИЯ ФУНКЦИИ ОТ

ТРЕХ ПЕРЕМЕННЫХ.

23

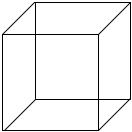
Введем геометрическое представление интервалов при n=3.

Для этого каждой из 8 конституент, сопоставив вершину трехмерного куба и двоичный эквивалент. При этом расположим вершины так, чтобы их двоичные представления отличались лишь в одном разряде.

Сопоставим коституенты с их двоичным эквивалентом:

24

Для представления функции на кубе ,участвующие интервалы выделяются.

и так как сложность уменьшилась с трех до двух, была произведена минимизация функции.

001 000

f(M1,М2,М3) = М 1М3 + М2М3 + М1 М 2 М 3

27

При выделении интервалов необходимо соблюдать дополнительные правила:

1)Все интервалы должны быть симметричны относительно исходных размеров карт;

2)Если 2 единицы находятся симметрично границы раздела они считаются соседними.

f(М1,М2,М3,М4,М5) = М2 М 3 М5 + М1 М 3 М4 М5 + М1 М 2 М3М4 М 5

f(М1,М2,М3,М4,М5) = М 1 М2 М 3 М 4М5 + М 1 М2 М 3 М4 М5 +

+М1М2 М 3 М 4 М5 + М1 М2 М 3 М4 М5 + М1 М 2 М 3 М 4 М5 +

+М1 М 2 М 3 М4 М5 + М 1 М2 М 3 М4 М 5 + М1 М2 М 3 М4 М 5 +

+М 1М2М3 М4 М 5 + М1 М2М3 М4 М 5 + М1 М 2М3 М4 М5 + М1 М 2М3 М 4 М5

28

f(М1,М2,М3,М4,М5) = М2 М 3 М5 + М2 М4 М 5 + М1 М 2 М5

Аппарат работы с картами и их преимущество.

1)Простота применения .

2)Наглядность расположения интервалов.

Недостатки:

1)Сложность работы возростает намного быстрее, чем увеличивается число элементов функции.

2)Трудоемкость алгоритмизации.

Исходя из недостатков следует, что для работы с функциями большего числа переменных нужны иные методы, причем они должны быть не графическими а аналитическими.

Для компьюторной технологии существует отличный от рассмотренного метода минимизации множеств ,который называется метод Квайна.

29

МИНИМИЗАЦИЯ ФУНКЦИИ МЕТОДОМ КВАЙНА.

Максимальный интервал I , который не содержится ни в каком другом интервале I Iк

где Iк - все интервалы функции, кроме I .

Рассмотрим функцию, заданную в СНФК:

Влевой части двоичный эквивалент конституент,а в правой присутствует ли она

вфункциональном представлении или нет. Кроме интервалов,представленные конституентами выделим другие интервалы более крупные.

Лемма.

Если в представление функции включен не максимальный интервал, то этот интервал может быть преобразован с помощью вычеркивания первичных термов.

Доказательство:

30

Исходя из определения , в функциональном представлении присутствует интервал, содержащий не максимум,а состоящий из некоторых первичных термов не максимальный интервал. Следовательно, максимальный интервал мажет быть получен вычеркиванием незначительных термов из немаксимального интервала.

М= А + В A = А + В

В– максимальный интервал

ВA В - не максимальный интервал

Вычеркиванием терма A – получим максимальный интервал.

Тупиковой формой –называется нормальная форма Кантора, из которой не может быть вычеркнут ни один терм без изменения представления функции.

Минимальной формой – называется тупиковаяформа, минимальной сложности Выражения для максимальных интервалов называются простыми

импликантами.

ТЕОРЕМА.

Все тупиковые ,а следовательно и минимальные формы содержатся в

объединении всех простых импликант.

Доказательство:

Из определения следует,что если вНФК присутствует неминимальный интервал

,то она не является тупиковой и не является минимальной.

Следовательно, тупиковой и минимальной формой есть объединение некоторых

простых импликант из множества всех простых импликант.

Согласно вышеуказанной теореме 1-й шаг метода Квайна состоит в выделении

простых импликант функции и составлении таблицы.

Строки соответствуют простым импликантам.

Столбцы – конституентам функции.