
MathCad_Metoda_Lab
.pdf
Продовження таблиці 7.2
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
14 |
|
− 2x4 + 6x3 + 38x2 − 54x − 180 |
− 0,5x |
|
7u 2 + 14 + 2u3 + 2u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u3 + 2u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
15 |
|
− 2x4 + 24x3 − 74x2 + 84x − 32 |
|
x − 7 |
|
|
24u 2 + 14 + 3u3 + 3u |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
9u3 + 6u + 3u 2 + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Таблиця 7.3 – |
|
Завдання до лабораторної роботи №7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Вар |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функція |
|
|||||||||||||
іан |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рівняння |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||||||||
1 |
(x + 3)4 + (x + 5)5 = 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = −3x3 + x2 + 50x − 6 |
|
||||||||||||||||||||||||||||||||||||||||
2 |
|
(x2 - x -1) x 2 −1 =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = x2e− x |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3 |
|
|
1 - 2cos (x) |
+ 2 tg(2x) = 3 |
|
|
|
|
|
|
|
|
|
|
f (x) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
+ 4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
sin(x) × cos(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
x3 − 2x2 − (a2 − a − 1)x + (a2 − a) = 0 |
|
|
|
f (x) = −x2 5 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
(x − 2)2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
5 |
|
a 2lg x−lg(6−x) = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = x ln 2 (x) |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
tg(x) |
|
= |
5 |
|
|
|
|
|
|
|
|
|
|
f (x) = 3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
6 |
|
|
|
|
1 + 3ctg(x) |
|
|
|
|
|
|
|
|
|
|
|
2x3 + 3x2 − 36x |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
+ tg(x) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
20 |
+ x |
|
|
|
|
+ x = 22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = |
|
|
|
|
|
14 |
|
|
|
|
|
|
|
||||||||||||||||||||
7 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
− 8x2 − 2 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||||||||||||||||||
8 |
|
lg(2x) + lg(2 - x) = lg(lg( p)) |
|
|
|
|
|
|
|
|
|
|
f (x) = x4e−x2 |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
sin(x) + |
|
|
|
|
|
|
|
|
|
|
|
+ sin(x) |
|
|
|
|
|
|
|
= 3 |
|
f (x) = |
x − 3 |
+ |
|
x − 8 |
+ 2,5 |
|
||||||||||||||||||||||||||
9 |
|
|
|
2 − sin 2 (x) |
2 − sin 2 (x) |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − 8 x − 3 |
|
|||||||||||||||
10 |
|
27x3 + 9x2 − 48x + 20 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = |
2x2 − 1 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + x2 |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
11 |
|
2lg(x + 3) = lg(a × x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = sin(2x) + cos(x) |
|
|||||||||||||||||||||||||||||||||||||||
12 |
|
sin(p |
|
) + sin(p × t) = |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = |
2x2 -17x + 21 |
|
|
|||||||||||||||||||||||||||||||||
t |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 + 6x - x2 |
|
||||||||||||||||
13 |
|
|
4 |
|
|
|
|
− |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = 1 − |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||||||||||||||||||||||||||||||
|
|
x 5 − 7x 5 + 6x−1 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
14 |
|
51− x − 51+ x = 24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = x2 + 5x − 6 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2x2 − 17x + 21 |
|
|||||||||||||||||||
15 |
|
|
tg(x) − sin(2x) − cos(2x) 1 − |
|
|
|
|
|
= 0 |
|
|
|
f (x) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
+ 6x2 − x |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|
|
|
|
|
7 |
|
||||||||||||||||||||||
40
7.3 Контрольні запитання
1.Пояснити призначення команд меню Symbolics, кнопок панелі інструментів
Symbolic.
2.Які символьні перетворення можна виконати у Mathcad?
3.Поясніть виконання кожного завдання.
4.Які переваги має виконання символьних перетворень із застосуванням символьного знака рівності і директив з панелі інструментів Symbolic?
Лабораторна робота №8 Розв’язання алгебраїчних, трансцендентних рівнянь, систем лінійних і
нелінійних рівнянь, нерівностей у Mathcad
Мета роботи: набуття навиків застосування Mathcad для розв’язання рівнянь, нерівностей, систем рівнянь.
8.1 Числове розв’язання рівнянь у Mathcad
Для числового розв’язання рівняння вигляду F (x) = 0 треба спочатку знайти
інтервал, що містить корінь або початкове наближення кореня (наприклад, за графіком функції F (x) ). Далі присвоїти змінній значення початкового наближення
і застосувати функцію root:
root(< вираз ( F (x) ) >, <ім’я змінної ( x )>) .
Ця функція повертає значення кореня. Якщо рівняння має декілька коренів, результат залежить від вибору початкового наближення.
Функцію root також можна використати, задавши замість початкового наближення координати a, b початку і кінця інтервалу, що містить корінь (вираз має
мати на кінцях інтервалу значення різного знака ):
root(<вираз ( F (x) ) >, <ім’я змінної ( x ) >, a, b).
Функція повертає корінь, що належить заданому інтервалу.
Для пошуку усіх коренів поліному степені n можна використати функцію polyroots:
polyroots(B),
де B – вектор (n+1) коефіцієнтів поліному, що складений за зростанням його степенів.
41
8.2 Символьне розв’язання рівнянь і нерівностей у Mathcad
Рівняння або нерівність у символьному вигляді можна розв’язати за допомогою команди Simbolics/Variable/Solve. Для цього треба записати рівняння або нерівність, використовуючи для вводу знаків операцій співставлення панель інструментів Boolean (або комбінації клавіш, що з’являються у спливаючих підказках), у виразі виділити змінну, відносно якої слід розв’язати рівняння (нерівність) і використати команду Simbolics/Variable/Solve.
Для пошуку символьного розв’язку може бути використана директива solve і символьний знак рівності
<рівняння (нерівність) > solve, < ім’я змінної >→
<вираз > solve, < ім’я змінної >→
У першому випадку визначається розв’язок рівняння (нерівності), у другому – значення змінної, при якому значення виразу дорівнює нулю.
Крім цього, для розв’язання рівняння у символьному і числовому вигляді можна застосувати блок розв’язання (п.п. 8.3, 8.4).
На рис. 8.1 наведений документ Mathcad, у якому розв’язано рівняння
5x3 + 7x2 − 9x − 3 = 0 .
8.3 Числове розв’язання систем рівнянь у Mathcad
Для розв’язання систем лінійних рівнянь вигляду A × X = B , де A - матриця коефіцієнтів, B - вектор вільних членів, X - вектор коренів в Mathcad є функція lsolve, яка повертає вектор коренів, а її аргументами є матриця коефіцієнтів і вектор вільних членів
lsolve( A, B) .
Систему лінійних або нелінійних рівнянь можна розв’язати із застосуванням блока розв’язання Given – find (minerr). Цей блок має таку структуру:
1.Завдання початкових наближень коренів.
2.Директива Given.
3.Рівняння.
4.Додаткові обмежуючі умови – задаються у вигляді нерівностей або рівнянь, які мають виконуватися для коренів системи.
5.Вираз із застосуванням функції find або minerr у вигляді
ім'я |
|
|
ім'я |
|
|
ім'я |
find( змінної1 |
, |
|
змінної 2 |
, ... |
змінної n ) |
|
або |
|
|
|
|
|
|
ім'я |
|
|
ім'я |
|
|
ім'я |
minerr( змінної1 |
, |
змінної 2 |
, ... |
змінної n ) . |
||
42

. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для відділення коренів будуємо графік функції |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Для застосування числових методів |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
за графіком визначаємо початкове |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
наближення x := −2 першого |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
5x |
+7x |
−9x−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
0 |
|
|
1 |
2 |
3 |
кореня і інтервал його існування |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a := −3 b := −2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x
Застосовуємо функцію root для пошуку кореня, задав інтервал його існування
( |
3 |
2 |
− 9x − 3 , x, −3 , −2 |
) |
= −2.117 |
|
|
|
|
root 5x |
+ 7x |
|
|
|
|
|
|||
або початкове наближення |
|
x := x |
root 5x |
+ 7x |
− 9x − 3 , x = −2.116 |
||||
|
0 |
( |
3 |
2 |
) |
||||
|
|
|
|
|
|
|
|
|
|
Для пошуку коренів поліному також можна застосувати функцію polyroots. Для цього формуємо вектор В коефіцієнтів поліному. Функція polyroots повертає вектор коренів
−3 |
|
−2.117 |
||
|
−9 |
|
||
B := 5u3 + 7u2 − 9u − 3 coeffs, u → |
|
polyroots(B) = −0.283 |
||
|
7 |
|
|
|
|
|
|
1 |
|
5 |
|
|
|
|
Для символьного роз'язання рівняння застосуємо директиву символьних перетворень solve
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
|
|||
5u3 |
+ 7u2 |
|
|
|
solve, u |
|
|
|
− 9u − 3 |
|
0 |
float, 5 |
→ −.28348 |
|
|||
|
||||||||
|
|
|
|
|
|
−2.1165 |
|
|
|
|
|
|
|
|
|
|
|
або блок розв'язання |
Given |
|
|
|
||
|
5u3 + 7u2 − 9u − 3 |
|
0 |
|||
|
|
|||||
|
|
|||||
|
Find(u) float, 5 → ( 1. −.28348 −2.1165 ) |
|||||
Знайдемо додатний корінь рівняння із застосуванням блока розв'язання |
||||||
у числовому вигляді |
|
|
|
|
|
|
u := 0 |
|
|
|
|
|
|
Given |
|
|
|
|
|
|
5u3 + 7u2 − 9u − 3 |
|
0 |
u > 0 |
|||
|
||||||
|
||||||
Find(u) = 1 |
|
|
|
|
|
|
. |
. |
|
Рисунок 8.1 – Приклад застосування Mathcad для розв’язання рівняння
43
Функції find і minerr повертають вектор розв’язку системи рівнянь. Різниця між функціями find і minerr полягає у тому, що функція find може бути застосована, якщо розв’язок існує. При спробі застосувати цю функцію у разі відсутності коренів виникає помилка. Функція minerr застосовується для пошуку значень змінних, що забезпечують мінімальну середньоквадратичну погрішність, навіть якщо точний розв’язок не існує.
|
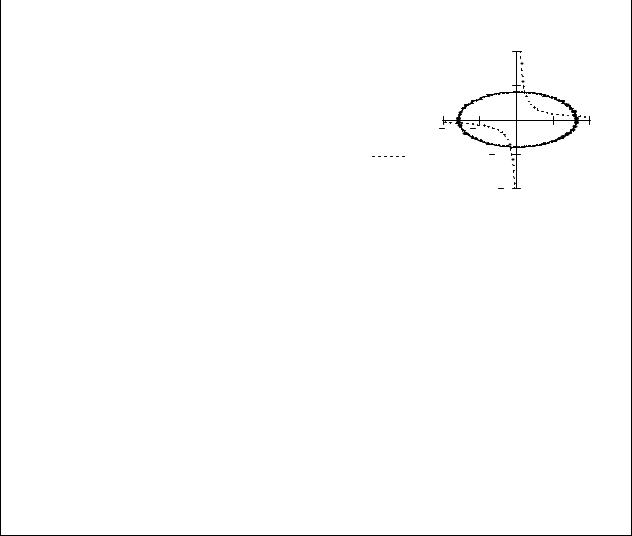
На рис.8.2 наведений документ |
Mathcad, |
у якому знайдений числовий |
||||||
|
x2 |
+ |
y |
2 |
= 1 |
|
|
||
|
|
|
|
|
|
|
|||
розв’язок системи нелінійних рівнянь 16 |
9 |
. |
|
||||||
|
|
|
|
||||||
|
|
y = |
1 |
|
|
|
|
||
|
|
x |
|
|
|||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
. |
|
|
Для числового розв'язання системи |
|
|
|
|
рівнянь необхідно знати початкові |
|
|
|
|
наближення змінних. Тому будуємо |
2 sin(t) |
|||
графіки еліпса (у параметричній формі) |
||||
і гіперболи, за нимиприблизно |
1 |
|
|
|
визначаємо координати x := 1 |
|
|
|
|
|
x |
|||
0 |
|
|||
y := 2 одієї з точок перетину графіків. |
|
|
|
|
0 |
|
|
|
|
Далі застосовуємо блок розв'язання
x := 1 |
y := 2 |
(початкові наближення) |
|
|
5 |
|
|
|
|
2.5 |
|
|
5 |
2.5 |
0 |
2.5 |
5 |
|
|
2.5 |
|
|
|
|
5 |
|
|
|
4 cos (t) , x |
|
|
|
Given |
|
|
|
|
|
|
|
||||
|
x2 |
+ y2 |
|
1 |
(рівняння) |
||||||
|
|
||||||||||
|
|
|
|
|
|||||||
16 |
4 |
|
|
||||||||
|
|
|
|||||||||
|
|
y |
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x |
|
|
|
||||
|
|
|
|
|
|
|
|||||
x1 |
|
|
|
|
|
||||||
:= minerr(x , y) |
(застосовуємо функцію minerr) |
||||||||||
|
|
||||||||||
y1 |
|
|
|
|
|
|
|
|
|||
Корені рівняння |
x1 = 0.504 |
|
y1 = 1.984 |
|||
Перевірка |
x12 |
+ y12 |
= 1 |
|
1 |
= 1.984 |
|
16 |
|
||||
|
4 |
|
|
x1 |
||
. |
|
|
|
. |
||
Рисунок 8.2 - Числове розв’язання системи нелінійних рівнянь (приклад)
8.4 Символьне розв’язання систем рівнянь у Mathcad
Для символьного розв’язання систем лінійних або нелінійних рівнянь можна застосувати директиву символьних перетворень solve. Для цього слід сформувати вектор, кожний елемент якого є одне з рівнянь системи. Далі виконати символьні перетворення таким чином:
44
|
< рівняння1 |
> |
|
< рівняння 2 |
|
|
> |
|
|
... |
solve, |
|
|
|
|
|
|
|
< рівняння n > |
|
ім'я ім'я
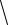 змінної1
змінної1 ,
,  змінної 2
змінної 2 , ...
, ...
 ім'я
ім'я  → змінної n
→ змінної n
Результатом буде матриця, елементи стовпців якої є значення коренів у тому порядку, як були записані імена змінних після директиви solve.
Блок розв’язання Given – find (minerr) можна застосувати для пошуку символьного розв’язку системи рівнянь. На відміну від числового розв’язку, в цьому випадку не треба задавати початкові наближення коренів і треба застосувати символьний знак рівності
ім'я |
|
ім'я |
|
ім'я |
) → |
find ( змінної1 |
, |
змінної 2 |
, ... |
змінної n |
Функція повертає матрицю, елементи рядків якої є значення коренів у тому порядку, як були записані імена змінних при визові функції find або minerr.
На рис.8.3 наведений документ Mathcad, у якому знайдений розв’язок системи нелінійних рівнянь з попереднього прикладу у символьному вигляді.
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
Для символьного |
|
x2 |
+ |
y2 |
|
|
|
|
|
3.97 |
|
.18 |
|
|
|
розв'язання |
|
|
1 |
|
solve, x, y |
|
−3.97 |
−.18 |
|
|
|||||
системи рівнянь |
16 |
|
4 |
|
|
|
|
||||||||
застосуємо |
z := |
|
1 |
|
|
float, 3 |
→ |
.51 |
2.01 |
|
|
||||
директиву solve |
|
|
x |
y |
|
|
|
|
|
−.51 |
−2.01 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
Кількість рядків матриці z |
|
|
i := ORIGIN .. rows(z) − 1 + ORIGIN |
|
|
||||||||||
дорівнює кількості |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
розв'язків системи рівнянь. |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
У кожному рядку матриці z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пара значень - перше - |
|
|
2 sin(t) |
|
|
|
|
2.5 |
|
|
|
|
|
|
|
значення х, друге - y. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Побудуємо графіки |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
функцій і отримані корені. |
|
x |
|
|
5 |
2.5 |
|
|
0 |
2.5 |
5 |
|
|||
|
|
|
|
|
|
|
|
||||||||
|
|
|
zi , ORIGIN+1 |
|
|
|
|
2.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
Знайдемо символьний |
Given |
|
|
|
|
4 cos (t) , x, zi , ORIGIN |
|
|
|
||||||
розв'язок системи |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
рівнянь за допомогою |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
+ y |
1 |
|
1 |
y |
|
|
|
|
|
|
|
|
||
блока розв'язання. |
|
|
|
|
|
|
|
|
|
||||||
|
16 |
|
4 |
|
|
x |
|
|
|
|
|
|
|
|
|
Матриця розв'язку v - |
v := Find(x, y) float, 3 |
|
3.97 |
|
−3.97 |
.51 |
−.51 |
|
|||||||
це транспонована |
→ |
|
−.18 |
|
|
−2.01 |
|
||||||||
матриця z |
|
|
|
|
|
|
.18 |
|
2.01 |
|
|||||
.
.
Рисунок 8.3 – Символьне розв’язання системи нелінійних рівнянь (приклад)
45

8.5Завдання
Уроботі треба:
1.Знайти усі корені багаточлену (графа 2 табл. 7.2) за допомогою функції polyroots. Отриманий розв’язок проілюструвати графічно: побудувати графік функції, що задана багаточленом і отримані корені у вигляді точок.
2.Знайти один корінь рівняння (графа 2 табл. 7.3), застосувавши функцію root. Для парних варіантів задати початкове наближення кореня, для непарних – межі інтервалу, що містить корінь. Для визначення початкового наближення і меж інтервалу існування кореня перетворити рівняння до вигляду F (x) = 0 і визначити
точку перетину функцією F (x) вісі абсцис, або до вигляду f (x) = ϕ(x) і визначити точку перетину функцій f (x) і ϕ(x) .
3.Застосувати функцію lsolve для розв’язання системи лінійних рівнянь
(табл. 3.1).
4.Визначити розв’язок системи рівнянь у символьному вигляді: для парних варіантів – системи лінійних рівнянь (табл. 3.3), для непарних варіантів – системи нелінійних рівнянь (графа 2 табл. 8.1). Для розв’язання системи рівнянь застосувати: директиву символьних перетворень solve (варіанти 1-5), функцію minerr (варіанти 6-10), функцію find (варіанти 10-15). Для непарних варіантів результат проілюструвати графічно.
5.Розв’язати систему рівнянь числовими методами із застосуванням блока розв’язання: для парних варіантів – системи нелінійних рівнянь (графа 2 табл. 8.1), для непарних варіантів – системи лінійних рівнянь (табл. 3.3). У варіантах 1-8 використати функцію find, у варіантах 9-15 – minerr. Для парних варіантів результат проілюструвати графічно.
6.Розв’язати нерівність з графи 3 табл. 8.1.
Таблиця 8.1 – Завдання до лабораторної роботи №8
Варі- Система рівнянь Нерівність ант
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||
|
x3 |
+ y3 = 7 |
|
|
|
1 |
|
+ |
|
|
|
5 |
|
|
|
|
> 1 |
|
|||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ x |
||||||||||||
|
x3 y3 = −8 |
|
|
2 − x 2 |
|
|
|
||||||||||||||||||||||
|
|
|
x x − 2 y = 36 |
|
|
x |
2 |
- 3x + 2 |
|
|
|
|
|
|
|||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
³1 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
4(x − 2 y) + ln(x) = 9 |
x2 + 3x + 2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
-1) |
2 |
+ ( y + 2) |
2 |
= 4 |
x |
4 |
- |
|
2x |
2 |
- 8 |
|
|
|
|
|
|||||||||||
3 |
(x |
|
|
|
|
|
|
|
< 0 |
|
|||||||||||||||||||
|
|
2x - y = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
x2 + 2x + 1 |
|
|
|
||||||||||||||||||||
|
x |
|
y |
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
+ |
|
|
= |
|
|
|
|
|
|
|
|
1 |
- |
3 |
|
< |
1 |
|
|
- |
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
4 |
y |
|
x |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
x2 |
4 |
|
|
x |
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x + y = 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
46 |
|
|
|
|
|
|
|
|
|
|
||

|
x + y = 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 - 4x > x - 3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
y = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x2 + y - 6 = 0 |
|
|
1 |
|
- |
|
|
|
|
|
|
2 |
|
|
£ |
1 − 2x |
|||||||||||||||||||||||||||||||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 1 |
|||||||||||
|
x2 + y 2 = 9 |
|
|
x + 1 |
|
|
x |
2 |
- x + 1 x3 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
+ |
|
1 |
|
= 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
y |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lg(7) - lg(-8x - x |
|
) |
> 0 |
|
|
||||||||||||||||||||||||||||||
7 |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lg(x + 3) |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
+ |
|
|
=13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
tg |
|
|
|
|
+ tg |
|
|
|
= 2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
2 - x < 2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
8 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 - x |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
ctg x + ctg y = -1,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
x - y = 5p/ 3 |
|
|
|
|
x - 3 |
|
|
|
|
|
|
³ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 - 5x + |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
sin(x) = 2sin( y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
+ |
|
1 |
|
|
= |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
y |
|
|
|
x |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x - 2x - 5x + 6 |
> 0 |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
2 |
|
+ x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
y |
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
x - 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
x + y |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
sin(x)sin( y) = 0,25 |
|
x2 (x + 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
11 |
|
|
|
|
|
|
|
x + y = p/ 2 |
|
|
|
5) + 5(3x + |
5) > 0 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
4 |
|
|
+ 4 |
|
|
|
|
|
= 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
12 |
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
+ 4x + 18) < 0 |
||||||||||||||||||||||||||||||
|
|
x + y =17 |
|
(x2 + 4x +10) |
- 7(x2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
13 |
x2 + y 2 = 9 |
|
|
x4 - 2x2 - 8 |
< 0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
x + y =1 |
|
|
x2 + 2x + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
+ y |
2 |
= 34 |
|
x |
3 |
|
- x |
2 |
+ x -1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
14 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
£ 0 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
x × y = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x + 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
xy + x =16 |
|
|
(x − 1)(x − 2)(x − 3) |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
>1 |
|
|
||||||||||||||||||||||||||||||
15 |
|
|
|
|
|
|
|
|
= 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x + 1)(x + 2)(x + 3) |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
y + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
8.6 Контрольні запитання
1.Яка функція Mathcad застосовується для числового розв’язання рівнянь? Як її застосувати?
2.Як знайти корені поліному?
3.Поясніть виконання кожного завдання.
4.Як розв’язати рівняння або нерівність у символьному вигляді?
5.Як отримати числовий розв’язок системи лінійних рівнянь?
47
6.Як застосувати блок розв’язку для числового і символьного розв’язання системи рівнянь?
7.Як застосувати директиву символьних перетворень solve для розв’язання системи рівнянь?
Лабораторна робота №9 Програмування у Mathcad
Мета роботи: набуття навиків застосування програмування для написання функцій користувача у Mathcad.
9.1 Програмування на Mathcad
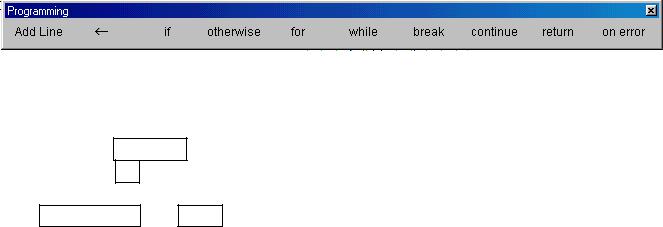
Mathcad дозволяє складати програмні блоки і використовувати такі блоки для виконання одноразових розрахунків, присвоювання значень змінним, означення функцій користувача. Програмний блок – це група операторів, об’єднана вертикальною лінією. Для вводу позначень і операторів програмного блоку використовується панель інструментів Programming (рис. 9.1).
Рисунок 9.1 – Панель інструментів Programming
Кожний оператор має бути розташований у окремому рядку програмного блока. Кнопка Add Line панелі інструментів Programming додає рядок програмного блока. Кнопка ← вводить оператор присвоювання, що має вигляд
ім’я змінної ← вираз
Усі змінні, значення яким присвоєно у документі Mathcad, по відношенню до програмного блока є глобальними. Змінні, значення яким присвоєно у програмному блоці є локальними. Локальні змінні поза програмним блоком не означені. Глобальні змінні діють і у програмному блоці, поки у ньому не введені локальні змінні з такими самими іменами.
Програмний блок повертає значення виразу (у тому числі і матричного), що записаний у останньому рядку програмного блоку. Програмний блок може повертати матриці, що містять вкладені масиви (тобто елементом матриці, що повертається може бути як проста змінна, так і матриця будь-якого розміру).
Упрограмному блоці можна використовувати оператори диференціювання, інтегрування, розрахунку суми, добутку, функції Mathcad, функції користувача, означені раніше, директиви символьних перетворень, оператори з панелі інструментів Programming.
Утабл. 9.1 дано опис операторів панелі інструментів Programming.
48

Таблиця 9.1 - Опис операторів панелі інструментів Programming
Умовний оператор
|
|
|
if |
|
|
|
|
if |
|
|
|
|
|
|
оператор 1 |
вираз 1 |
|
|
|
|
вираз 1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
оператор 2 |
|
|
або |
|
|
програмний блок 1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
оператор 2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оператор працює таким чином:
1.Розраховується значення логічного або арифметичного виразу 1.
2.Якщо значення арифметичного виразу відрізняється від 0 або значення логічного виразу дорівнює 1 (істина) виконується оператор 1 (або програмний блок 1 – якщо у гілці “ так” має бути декілька операторів).
3.Якщо значення виразу 1 дорівнює нулю (хибність) – виконується оператор 2.
Гілка “ ні” умовного оператора
|
|
otherwise |
|
|
otherwise |
|
|
оператор 3 |
або |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
програмний блок 3 |
|
|
|
|
|
|
|
|
Оператор може бути на місці оператора 2, слідом за умовним оператором. Якщо вираз 1 у попередньому операторі if приймає значення 0, виконується оператор 3 (або програмний блок 3). Якщо значення виразу 1 у попередньому операторі if відрізняється від нуля, оператор 3 буде пропущено.
Оператор циклу for
for ім’я змінної-параметра циклу a,b .. c
оператор або програмний блок (тіло циклу)
де a, b, c - перше, друге и кінцеве значення параметра циклу.
Тіло циклу виконується поки параметр циклу приймає значення з заданого діапазону.
Оператор циклу while
while вираз 1
оператор або програмний блок (тіло циклу)
Тіло циклу виконується поки значення виразу 1 відмінне від нуля. Вираз 1, як і у умовному операторі, може бути логічним або арифметичним.
|
continue |
|
Передчасне завершення поточної ітерації |
||||
|
|
|
|
|
|
|
циклу. |
|
break |
|
Передчасний вихід з циклу. |
||||
|
|
|
|
|
|
Оператор повернення |
|
|
return |
|
|
|
|
|
Передчасне завершення програмного блоку |
|
вираз |
|
|
|
|||
|
|
|
|
з поверненням значення виразу, що |
|||
|
|
|
|
|
|
|
записаний після оператору повернення. |
|
|
|
|
|
|
Обробка помилок |
|
|
|
|
on error |
|
|
Якщо під час розрахунку значення виразу 2 |
|
|
вираз 1 |
вираз 2 |
|
||||
|
|
виникла помилка, розраховується значення |
|||||
|
|
|
|
|
|
|
виразу 1. |
49
