Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донецкий национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Научный пособник том 2All Tom 2 UA

.pdf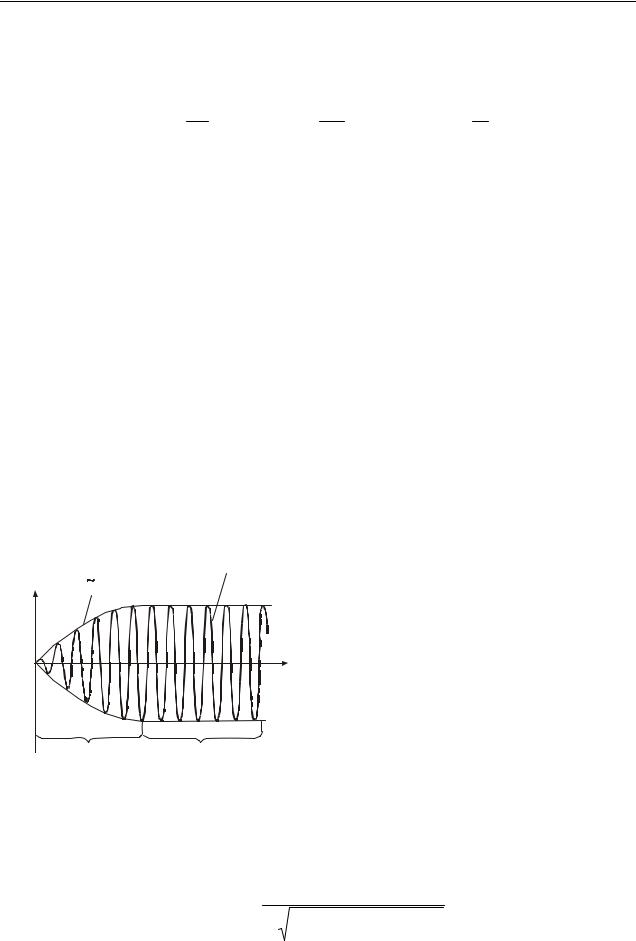

Скачиваний:

174

Добавлен:

03.03.2016

Размер:

3.77 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 224 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

										Коливання
або						2
		&&	&			2					(7.3)
		x	+ 2βx + ω0 x = f0 cos Ωt ,								(7.3)
де		= F0 ,				r ,		ω02 = k .
	f0	= F0 ,	β =			r ,		ω02 = k .
		m				2m		m
	Рівняння (7.3) є диференціальним рівнянням вимушених механічних ко-
ливань. З теорії диференціальних рівнянь відомо, що загальний розв’язок дано-
го	неоднорідного	диференціального				рівняння		дорівнює	сумі	загального
розв’язку відповідного однорідного рівняння і частинного розв’язку неоднорід-
ного:
			x(t) = x1 (t) + x2 (t) .
	Загальний розв’язок однорідного рівняння вже відомий (див. формулу
(6.4)):
		x (t)= A e−βt cos(ωt + ϕ					0	).
		1	0				0
	Можна показати, що частинний розв’язок, якій задовольняє правій части-
ні рівняння (7.2), має вигляд:
			x2 (t)= Acos(Ωt + ϕ).
	Амплітудне значення x (t) яке дорівнює A e−β t після початку вимуше-
		1					0
		x=Acos(Ωt+ϕ			)	них коливань більш менш швидко
	e−βt	x=Acos(Ωt+ϕ		0	)	зменшується. Отже, через деякий час τ
x	e−βt			0		після початку коливань вільні коли-
						вання маятника практично припиня-
						ються: x(t) ≈ x2 (t) .			Маятник		перехо-
						дить в стан встановлених вимушених
			t			коливань, які здійснюються з частотою
			t			змушуючої сили (див. рис. 7.1):
						змушуючої сили (див. рис. 7.1):
								x(t)= Acos(Ωt + ϕ),			(7.4)
	перехідний	усталені				де φ − є величиною відставання за фа-
	процес	коливання				де φ − є величиною відставання за фа-
	Рисунок 7.1					зою вимушеного коливання					від зму-
	Рисунок 7.1					шуючої сили. Амплітуда цих коливань
						шуючої сили. Амплітуда цих коливань
						А і значення φ визначаються як пара-
метрами системи (m, ω0), так і параметрами змушуючої сили (F0, Ω).

F0
A = m (ω02 − Ω2 )2 + 4β2Ω2	(7.5)

Коливання

tgϕ = −	2βΩ		.	(7.6)
	ω2	− Ω2

	0

Графік залежності амплітуди А вимушених коливань від частоти Ω змушуючої сили (тобто амплітудно-частотна характеристика), має вигляд, представлений на рис. 7.2.

Якщо Ω = 0 то ϕ = 0 . В цьому випадку
A = A	=	F0	=	F0	.	(7.7)
		mω02
ст				k

Амплітуду Аст називають статичним зсувом (статичною амплітудою) маятника від положення рівноваги під дією сталої сили F0.

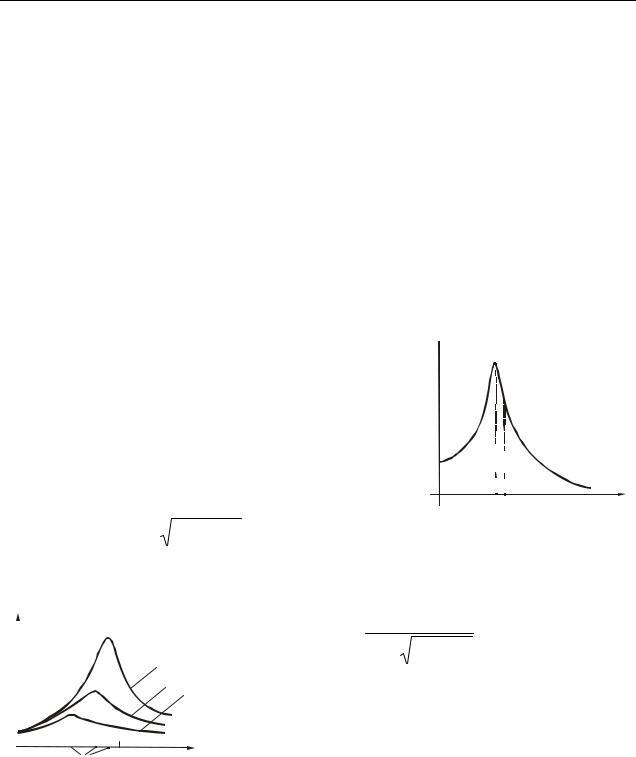
При деякій частоті Ωp , званою резонансною, амплітуда досягає максима-

льного значення Ар.

Явище різкого зростання амплітуди вимушених коливань при наближенні частоти змушуючої сили до власної частоти ω0 назива-

ється резонансом.

Щоб визначити резонансну частоту Ωp

A Ap

треба досліджувати вираз (7.5) на екстремум.

Aст

При цьому для резонансної частоти випливає

наступний вираз:

ω0

ω02 − 2β2 .

(7.8)

Ωр =

Рисунок 7.2

Підставивши це значення частоти в (7.5),

отримаємо вираз для резонансної амплітуди:

β< β <β

Ap =

(7.9)

β1

2mβ ω02 − β2

β2

β3

З (7.9) випливає, що при β = 0 (сил опору не-

має) амплітуда при резонансі оберталася б в нескін-

ченність. Резонансна частота при цьому співпала б з

Ωp

ω0

власною частотою ω0.

Рисунок 7.3

З (7.8) і (7.9) також випливає, що чим менше β,

тим

вище максимум

кривої і правіше

зміщений

(рис. 7.3).

Для β <<ω0 відношення резонансної амплітуди до статичної дорівнює до-

бротності системи:

Aр

= Q .

(7.10)

ст

Коливання

7.2 Вимушені коливання в коливальному контурі

Щоб викликати вимушені коливання в коливальному контурі, потрібно включити послідовно з елементами контуру змінну ерс (рис. 7.4):

ε(t) = ε0 cos Ωt ,

(7.11)

де ε0 – амплітудне значення ерс.

Отримаємо диференціальне рівняння вимушених коливань, застосувавши закон збереження енергії. У ліву частину рівняння (6.7) (див. § 6, п. 6.2) додамо елементарну роботу, яку здійснює джерело ерс:

δA = εI dt .

(7.12)

Рівняння (6.7) прийме вигляд:

− d (Wел +Wм )+ δA = δQ .

(7.13)

~ε

Провівши такі ж перетворення, як в п. 6.2, отримаємо

Рисунок 7.4

наступне рівняння:

d 2q

q = ε0

cosΩ t

(7.14)

dt2

L dt

або:

ε0

cosΩ t .

(7.15)

q + 2βq + ω0q =

Тут β і ω0 визначаються тими ж формулами, що у разі згасаючих коли-

вань.

Рівняння (7.15) є диференціальним рівнянням вимушених електромагнітних коливань. Воно має той же вигляд, що і диференціальне рівняння вимушених механічних коливань (7.3). Отже, його розв’язок також представимо у вигляді:

q(t) = q1(t) + q2 (t) ,

де q1(t) = q01e−βt cos(ωt + ϕ0 ) − загальний розв’язок однорідного диференціального рівняння;

q2 (t)= q0 cos(Ωt + ϕ) − частинний розв’язок даного неоднорідного рів-

няння.

При встановлених вимушених коливаннях заряд змінюється за гармонічним законом:

q(t)= q0 cos(Ωt + ϕ).

(7.16)

Амплітудне значення заряду q0 і зсув фаз φ знаходяться за формулами, аналогічними для механічних коливань:

Рисунок 7.5

Коливання

ε0

(7.17)

1 2

L (ω0

− Ω

) + 4β

2 +

ΩL −

ΩC

tgϕ = −

2βΩ

(7.18)

ω02 − Ω2

ΩL

−

ΩC

У формулах (7.17) і (7.18) зроблена заміна:

β =

ω0 =

1 .

Графік залежності заряду q від частоти Ω співпадає з графіком А =f(Ω) для вимушених механічних коливань (див. рис. 7.3).

Сила струму в коливальному контурі при встановлених коливаннях:

	dq				π
I =		= −q0	Ωsin(Ωt + ϕ)= I0 cos	Ωt + ϕ +	,	(7.19)
I =	dt	= −q0	Ωsin(Ωt + ϕ)= I0 cos	Ωt + ϕ +	,	(7.19)
	dt				2

де I0 = q0Ω − амплітуда сили струму, ϕ = ϕ0 + π2 зсув фаз між струмом і при-

кладеною напругою.

R1=0

	R 2	R 2< R 3




	R 3











ω0		Ω

Графіки залежності сили струму I0 від Ω при різних R називаються резонансними кривими (рис. 7.5). Резонансна циклічна частота Ωр, відповідна максимуму амплітуди

сили струму в контурі, не залежить від активного опору R:

Ωр = ω0 =	1 .	(7.20)
	LC

Явище резонансу грає велику роль в техніці. Його використовують в акустиці для підсилення звучання музичних інструментів, в електротехніці – для вимірюван-

ня частоти струму, в радіотехніці – для виділення потрібного сигналу з інших, що відрізняються частотою, а також в багатоканальній телеграфії і телефонії.

Резонанс може бути причиною аварій і катастроф. Періодичні поштовхи від поршневих машин, силових валів турбін, пропелерів передаються на фундаментальні і інші частини машин. Тому, наприклад, власна частота вібрацій корпусу корабля або крила літака повинна значно відрізнятися від частоти збуджуючої сили, обумовленої обертанням силових гвинтів. Амплітуду небезпечних резонансних коливань також зменшують, збільшивши коефіцієнт загасання (це робиться в амортизаторі автомобіля). У цьому випадку явище резонансу стає непомітним.

Таблиця 7.1 Зіставлення рівнянь, що описують механічні і електромагнітні коливання

Система

Фізична

Тип коливань

Умови

Диференціальне

Характеристики

модель

а) за природою

необхідні

рівняння і його

коливань

б) за характером

для здійснення

розв’язання

коливань

Замкнена

Пружинний

а) механічні

1. Наявність

&x&+ ω02 x = 0

= 2π

консерва-

маятник

б) гармонічні

пружної або

x(t) = Acos(ω0t + ϕ0 )

тивна

квазіпружної сили

Fпр= − kx

Фізичний

а) механічні

2. Наявність

α&& + ω02α = 0

= 2π

mgl

маятник

б) гармонічні

обертаючого моменту

α(t) = αmax cos(ω0t + ϕ0 )

М, який прагне

ω0 =

mgl

повернути маятник в

положення рівноваги,

Математичний

= 2π

а) механічні

і аналогічний в цьому

маятник

б) гармонічні

квазіпружній силі.

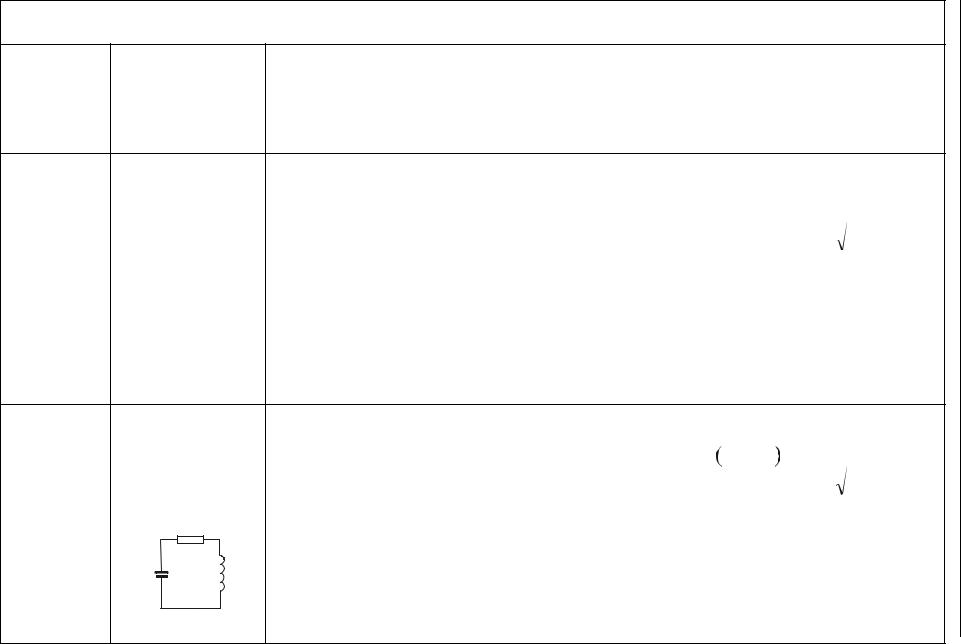
Замкнена

коливальний

а) електромагнітні

1. Наявність

&&+ ω2

консерва-

контур

б) гармонічні

конденсатора

0 q

q = qmax cos(ω0t + ϕ0 )

тивна

ємністю С і

ω0 =

котушки

індуктивністю L.

2. Активний опір

контуру R = 0

Коливання

Продовження таблиці 7.1 Зіставлення рівнянь, що описують механічні і електромагнітні коливання

Система	Фізична
	модель

Замкнена Пружинный дисипативна маятник

Замкнена Коливальний дисипативна контур

	R
C	L

Тип коливань

Умови

Диференціальне

Характеристики

а) за природою

необхідні

рівняння і його

коливань

б) за характером

для здійснення

розв’язання

коливань

а) механічні

1. Наявність

&&+

β&

+ ω

2π

2 x

0 x

б) затухаючі

пружної або

x(t) = A e−βt

T = ω

квазіпружної сили

cos(ωt + ϕ

)

Fпр= − kx

ω = ω02 −β2

β =

2. Наявність сили

опору (тертя)

Fоп= − rv.

а)електромагнітні

1. Наявність

&&+

β &

+ ω

2π

2 q

0 q

б) затухаючі

зарядженого

e−βt

T = ω

q(t) = q

cos ωt + ϕ

конденсатора

ω =

ω2

−β2

ємністю С і

котушки

β =

індуктивністю L.

2. Активний опір

контура R≠0.

Коливання

Продовження таблиці 7.1 Зіставлення рівнянь, що описують механічні і електромагнітні коливання

Система

Фізична

Тип

Умови

Диференціальне

Характеристики коливань

модель

коливань

необхідні

рівняння і його

для здійснення

розв’язання

коливань

Не замкнена

Пружинний

а) механічні

1. Наявність пружної

&&+ β&

+ ω

дисипативна

маятник

б) вимушені

або квазіпружної

2 x

0 x

f0 cos t

A =

m (ω02 + Ω2 )2 + 4β2Ω2

x(t)

A cos(

)

сили Fпр= − kx

2. Наявність сили

tgϕ = −

2βΩ

опору (тертя)

ω2 − Ω2

Fоп= − rv.

3. Наличие

вынуждающей силы

F(t) = F0cos Ωt.

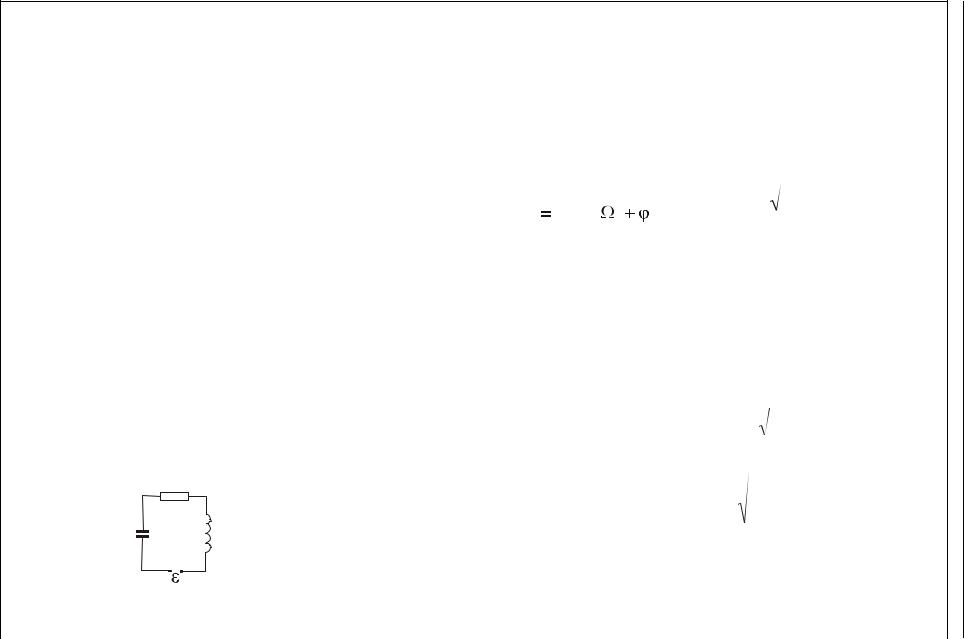
Не замкнена

Коливальний

а) електро

1. Наявність

ε0

дисипативна

контур

магнітні

зарядженого

q +

2βq + ω0 q =

cosΩ t

(ω02

+ Ω2 )2

+ 4β2

Ω2

б) вимушені

конденсатора

q(t) = q0 cos(Ωt + ϕ)

ємністю С і

котушки

Ω R

2 +

ΩL

−

індуктивністю L.

ΩC

2. Активний опір

2βΩ

контуру R ≠ 0.

tgϕ = −

3. Наявність змінної

− Ω

ерс

ω0

ΩL −

ΩC

ε(t)=ε0cos Ωt.

Коливання

Хвилі

Розділ 2. Пружні хвилі

§8 Загальні відомості про хвилі

Хвиля – це процес розповсюдження збурень в просторі, якій супроводжується перенесенням енергії.

Збурення (ξ) – це відхилення якої-небудь фізичної величини, що характеризує стан системи, від значення, яке вона мала при знаходженні системи в стані рівноваги.

Ми розглядатимемо збурення, які носять коливальний характер, тому можна дати більш вузьке визначення хвилі.

Хвиля – це процес розповсюдження коливань в просторі.

8.1 Класифікація хвиль

Залежно від фізичної природи джерела коливань хвилі поділяють на:

–механічні (звукові, ударні, сейсмічні і так далі);

–хвилі на поверхні рідини;

–електромагнітні (шкала електромагнітних хвиль в інтервалі від радіохвиль до гамма-випромінювання).

Механічними хвилями називаються механічні збурення, що виникають в

пружному середовищі, тому механічні хвилі мають другу назву – пружні хвилі. Поверхневі хвилі розповсюджуються уздовж вільної поверхні рідини або уздовж поверхні двох рідин, що не змочуються. В утворенні цих хвиль визначальну роль грають сили поверхневого натягу і сили тяжіння. У поверхневих хвилях частинки рідини одночасно здійснюють поперечні і поздовжні коливан-

ня, описуючи еліптичні або складніші траєкторії.

Залежно від взаємної орієнтації напряму коливань і напряму розповсюдження хвиль розрізняють:

–поперечні хвилі;

–поздовжні хвилі.

Хвиля називається поперечною, якщо напрям коливань частинок середо-

вища перпендикулярний напряму розповсюдження хвилі (рис. 8.1 а).
ξ				Хвиля називається поздовжньою,	якщо
ξ				напрям коливань частинок середовища співпа-
				напрям коливань частинок середовища співпа-
		v	а)	дає з напрямом розповсюдження	хвилі
				(рис. 8.1 б).
				(рис. 8.1 б).
				Пружні поперечні хвилі можуть виник-
				Пружні поперечні хвилі можуть виник-
				нути лише в середовищі, що має опір зсуву,
	ξ			тому у рідкому і газоподібному середовищах
	ξ		б)	можливе виникнення тільки поздовжніх хвиль.
		v		У твердому середовищі можливе виникнення
		v		У твердому середовищі можливе виникнення

	Рисунок 8.1	як поздовжніх, так і поперечних хвиль.
		При розповсюдженні від джерела коли-

	вань хвильовий процес охоплює все нові області простору.

Хвилі

Область простору, в якій існує хвильовий процес (збурення), називається хвильовим полем. Геометричне місце точок, до яких доходять коливання до моменту часу t, називається фронтом хвилі. Фронт хвилі є тією поверхнею, що відокремлює частину простору, яка вже залучена до хвильового процесу, від області, в якій коливання ще не виникли. Залежно від геометрії фронту хвилі поділяють на:

–плоскі (рис 8.2 а);

–сферичні (рис 8.2 б).

		Стрілки на ри-
		сунку	указують	на-
		прям розповсюджен-
		ня хвилі. Плоскі хви-
		лі виникають		від
		плоского або вида-
фронт хвилі	фронт хвилі	леного	джерела.	Їх
фронт хвилі		хвильовими фронта-
а)		хвильовими фронта-
а)	б)	ми є площини. Сфе-
	Рисунок 8.2	ми є площини. Сфе-
	Рисунок 8.2	ричні	хвилі виника-
		ричні	хвилі виника-

ють від точкового джерела в просторі. Їх хвильовими фронтами є сфери.

8.2 Характеристики хвиль

Особливе значення в теорії хвиль має уявлення про гармонічну хвилю, тобто нескінченну синусоїдальну хвилю, в якій всі зміни стану відбуваються за законом синуса або косинуса (рис. 8.3). Такі хвилі могли б розповсюджуватися в однорідному середовищі без спотворення форми.

Основними характеристиками хвилі є:

Довжина хвилі (λ) – відстань між найближчими точками, що коливаються в однаковій фазі (рис. 8.3).

Період коливань (T) – час, протягом якого здійснюється один повний цикл коливань.

Амплітуда (A) – максимальне відхилення фізич-

	ної величини від положення рівноваги.
Рисунок 8.3	Довжина хвилі і період зв’язані співвідношенням:
Рисунок 8.3
	λ = vT ,	(8.1)

де v – швидкість розповсюдження хвилі.

Ця формула справедлива для хвиль будь-якої природи. З використанням співвідношення (8.1) можна дати інше визначення довжини хвилі.

Довжина хвилі – це відстань, на яку розповсюджується фронт хвилі за час, що дорівнює періоду коливань.

Замість періоду Т часто користуються частотою ν, яка дорівнює числу коливань за одиницю часу ν = T1 . З (8.1) отримаємо:

Хвилі

λ = v .	(8.2)
ν

Нагадаємо, що період вимірюється в секундах, частота – в герцах.

§9 Плоска монохроматична хвиля

Гармонічна хвиля називається монохроматичною, якщо її частота ν і амплітуда А з часом не змінюються. Якщо фронтом хвилі є площина, то хвиля називається плоскою.

9.1 Рівняння плоскої монохроматичної хвилі

Рівнянням хвилі називається вираз, який визначає, як зсув ξ частинки, що коливається, залежить від координати x і часу t: ξ = ξ(x t,). Вісь 0x сумістимо з напрямом розповсюдження хвилі. Хвильові поверхні плоскої хвилі будуть перпендикулярні осі x (рис. 9.1).

Коливання точок, які лежать у площині x =0, тобто коливання джерела, мають вигляд:

ξ(0,t)= Acosωt .

Щоб пройти шлях від площини x=0 до площини з довільною координатою x, потрібний час

x=0

хвильовий

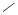фронт

0		x
	x= vτ

τ = vx ,

де v – швидкість переміщення фронту хвилі.

Це означає, що коливання частинок, які лежать у площині x, відставатимуть за часом на τ. Їх рівняння має вигляд:

Рисунок 9.1		x
	ξ(x,t)= Acos ω t −		.	(9.1)

		v

Рівнянню (9.1) можна надати інший вигляд. Для цього введемо величину

k =	2π	,	(9.2)
	λ

яка називається хвильовим числом. Хвильове число показує, скільки довжин хвиль укладається на відстані 6,28 м. З урахуванням (9.2), а також того, що

ω =

або

2π	T	, а λ = vT	отримаємо:
	T			2πt		2πx
				2πt	−	2πx
			ξ(x,t)= Acos	T	−	λ	,
				T		λ
			ξ(x,t)= Acos (ωt − k x).					(9.3)

<<< < Предыдущая 1 2 34 / 224 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
03.03.2016909.97 Кб34МУ_ТОБ_2013_БС_ТТР.pdf
#
03.03.20162.07 Mб205Навчальний посибник.pdf
#
03.03.20161.98 Mб151навчатьный посибник 2.pdf
#
03.03.2016177.15 Кб4налоги.docx
#
03.03.20163.85 Mб118Научное помсобие 1All Tom 1 UA.pdf
#
03.03.20163.77 Mб174Научный пособник том 2All Tom 2 UA.pdf
#
03.03.201614.29 Mб48НГ_МУ_6_35.pdf
#
03.03.201629.11 Кб63Нетрадиционные источники энергии.docx
#
03.03.2016497.27 Кб3НИРС -ВИКА -2.3(23.09).docx
#
03.03.201656.21 Кб3НИРС.docx
#
03.03.2016465.92 Кб59Новий Документ Microsoft Word.doc