
- •1 Описание формальной модели алгоритма на основе рекурсивных функций
- •2 Описание аналитической модели алгоритма в виде элементарных машин тьюринга и композиции мт
- •3 Разработка аналитической и программной модели алгоритма для распознающей машины тьюринга
- •4 Разработка аналитической модели алгоритма с использованием нормальных алгоритмов маркова
- •01X110d
3 Разработка аналитической и программной модели алгоритма для распознающей машины тьюринга
3.1 Формальное определение распознающей машины Тьюринга
Программная модель была написана с целью распознания языка
L
= { wwRwR
│w
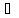 {0,1}*
}. Обработка слова не является трудоемкой
и не потребует более одной ленты.
{0,1}*
}. Обработка слова не является трудоемкой
и не потребует более одной ленты.
/*Вход в машину Тьюринга. Установка разделителя в конце слова*/
 0->
0-> 0R
0R
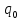 1->
1-> 1R
1R
 ~->
~->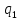 *L
*L
/*Замена "1" и "0" на символы "а" или "b"*/
 0->
0-> aL
aL
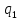 1->
1->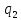 bL
bL
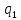 a->
a-> aL
aL
 b->
b->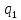 bL
bL
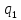 *->
*->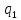 *L
*L
 d->
d->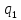 dL
dL
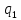 ~->
~->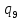 ~R
~R
/*Замена "1" и "0" на "а" и "b" */
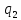 0->
0-> aL
aL
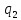 1->
1->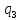 bL
bL
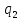 ~->
~-> ~R
~R
/*Замена "1" и "0" на "а" и "b"*/
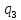 0->
0-> aR
aR
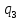 1->
1->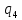 bR
bR
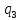 ~->
~-> ~R
~R
/*Возврат в конец слова и установка признака mod 3*/
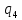 a->
a-> aR
aR
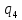 b->
b->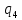 bR
bR
 *->
*->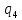 *R
*R
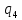 ~->
~->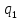 dL
dL
 d->
d->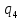 dR
dR
/*Повторение действий предыдущих состояний, пока не встретим пустой символ*/
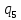 a->
a->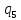 aR
aR
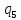 b->
b-> bR
bR
 *->
*-> *R
*R
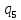 d->
d->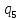 dR
dR
 ~->
~->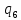 ~L
~L
//Если преждевременно находим пустой символ возвращаемся назад
 d->
d-> ~L
~L
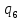 *->
*->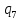 *R
*R
Рисунок 3.1, лист 1 – Система команда МТ
/*Установка признака "0" - слово не является словом языка*/
 ~->
~->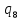 0L
0L
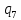 d->
d->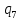 ~L
~L
 *->
*->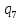 *R
*R
//Замена всех разделителей (кроме "*") на "1" или "0". //Конец работы машины
 *->
*-> *L
*L
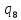 b->
b->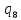 1L
1L
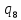 a->
a-> 0L
0L
 d->
d-> dR
dR
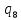 n->
n->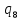 1L
1L
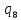 0->
0-> 0L
0L
 1->
1->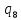 1L
1L
 p->
p->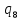 0L
0L
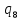 o->
o-> 1L
1L
 h->
h-> 0L
0L
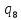 ~->
~-> ~R
~R
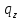 ~->
~->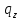 ~R
~R
/*Если слово подходит по количеству символов - меняем разделитель
Возврат в конец слова*/
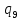 a->
a->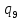 aR
aR
 b->
b->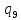 bR
bR
 *->
*->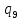 *R
*R
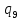 d->
d->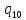 mL
mL
 m->
m-> mR
mR
 p->
p-> pR
pR
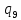 n->
n-> nR
nR
 h->
h->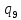 hR
hR
 o->
o->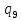 oR
oR
 ~->
~->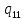 ~L
~L
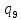 1->
1->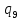 1R
1R
 0->
0-> 0R
0R
//Проходим снова влево, устанавливаем новый разделитель для последнего символа слова
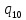 a->
a-> pR
pR
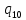 b->
b->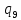 oR
oR
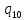 m->
m->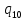 mL
mL
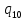 *->
*->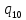 *L
*L
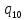 p->
p-> pL
pL
 o->
o->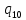 oL
oL
 0->
0->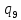 hR
hR
 1->
1->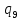 nR
nR
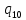 n->
n-> nL
nL
 h->
h-> hL
hL
/*Проходим снова влево, устанавливаем новый разделитель для предпоследнего символа слова*/
 m->
m-> dL
dL
 n->
n-> nR
nR
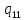 *->
*-> *R
*R
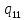 ~->
~-> ~L
~L
 d->
d-> dR
dR
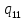 o->
o->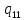 oR
oR
 p->
p-> pR
pR
 h->
h->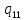 hR
hR
//Проходим снова влево, устанавливаем новый разделитель символа слова
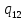 h->
h->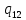 hL
hL
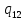 *->
*->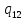 *L
*L
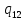 b->
b-> nR
nR
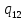 n->
n-> nL
nL
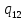 a->
a-> hR
hR
 p->
p-> pL
pL
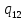 o->
o->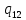 oL
oL
 d->
d-> dL
dL
 m->
m->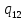 mL
mL
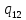 1->
1-> 1R
1R
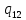 0->
0->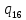 0R
0R
Рисунок 3.1, лист 2 – Система команд МТ
//Проверка на равенство двух последних триад
 d->
d->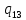 dL
dL
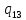 *->
*->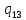 *L
*L
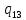 p->
p-> 0R
0R
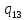 o->
o-> 1R
1R
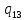 0->
0-> 0L
0L
 1->
1->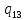 1L
1L
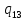 a->
a-> aR
aR
 b->
b->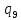 bR
bR
 ~->
~->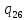 ~R
~R
// Если первый был символ "p"
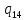 *->
*-> *L
*L
 0->
0-> 0L
0L
 1->
1->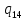 1L
1L
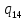 o->
o-> oL
oL
 p->
p->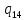 pL
pL
 h->
h-> 0R
0R
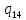 n->
n-> nR
nR
//Проход вправо до “*”
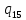 p->
p->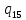 pR
pR
 o->
o->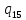 oR
oR
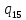 1->
1->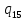 1R
1R
 0->
0-> 0R
0R
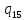 *->
*-> *L
*L
//Проверка на реверс двух первых триад
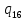 0->
0->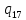 uL
uL
 1->
1->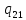 vL
vL
 u->
u->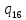 uL
uL
 n->
n->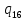 nL
nL
 h->
h->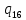 hL
hL
 v->
v->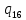 vL
vL
 ~->
~->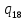 ~R
~R
//Если первый был символ “0”
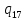 0->
0-> 0L
0L
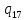 1->
1-> 1L
1L
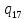 b->
b-> bL
bL
 a->
a-> aL
aL
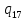 v->
v->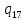 vL
vL
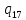 u->
u-> uL
uL
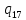 ~->
~-> ~R
~R
//Проход в конец слова
 0->
0->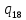 0R
0R
 1->
1->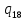 1R
1R
 o->
o->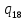 oR
oR
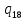 p->
p-> pR
pR
 n->
n->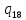 nR
nR
 a->
a-> aR
aR
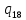 b->
b->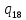 bR
bR
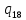 h->
h->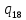 hR
hR
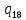 u->
u->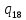 uR
uR
 v->
v-> vR
vR
 *->
*-> *R
*R
 d->
d-> dR
dR
 m->
m-> mR
mR
 ~->
~-> ~L
~L
//Замена разделителей (n->1)
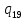 *->
*->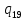 *L
*L
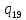 0->
0-> 0L
0L
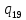 1->
1->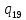 1L
1L
 o->
o->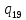 oL
oL
 p->
p->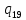 pL
pL
 n->
n-> 1R
1R
 h->
h-> hR
hR
//Проход вправо до “*”
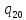 p->
p-> pR
pR
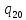 o->
o-> oR
oR
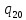 1->
1->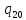 1R
1R
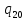 0->
0->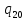 0R
0R
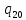 *->
*-> *L
*L
// Проход вправо до “~”
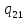 0->
0->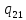 0L
0L
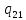 1->
1->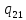 1L
1L
 v->
v->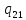 vL
vL
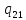 u->
u-> uL
uL
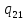 b->
b->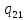 bL
bL
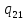 a->
a->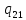 aL
aL
 ~->
~->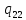 ~R
~R
Рисунок 3.1, лист 3 – Система команд МТ
//Замена старого символа на новый (b->v)
 b->
b-> vR
vR
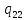 v->
v->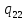 vR
vR
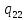 u->
u->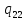 uR
uR
 a->
a-> aR
aR
//Проход вправо до границы слова
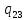 b->
b-> bR
bR
 a->
a->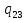 aR
aR
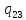 0->
0->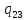 0R
0R
 1->
1->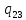 1R
1R
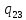 v->
v->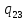 vR
vR
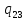 u->
u->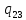 uR
uR
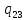 n->
n-> nL
nL
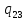 h->
h-> hL
hL
//Замена старого символа на новый (a->u)
 a->
a-> uR
uR
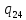 v->
v-> vR
vR
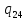 u->
u-> uR
uR
 b->
b-> bR
bR
//Проход вправо до границы слова
 b->
b-> bR
bR
 a->
a-> aR
aR
 0->
0-> 0R
0R
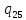 1->
1->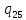 1R
1R
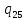 v->
v->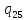 vR
vR
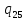 u->
u->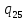 uR
uR
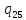 n->
n->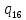 nL
nL
 h->
h-> hL
hL
//Очистка всех признаков
 d->
d->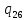 ~L
~L
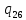 m->
m->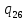 ~L
~L
 *->
*->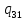 *R
*R
//Проход в конец слова
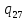 0->
0->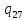 0R
0R
 1->
1-> 1R
1R
 o->
o->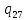 oR
oR
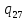 p->
p->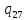 pR
pR
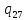 n->
n-> nR
nR
 a->
a-> aR
aR
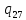 b->
b->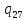 bR
bR
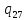 h->
h-> hR
hR
 u->
u->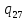 uR
uR
 v->
v->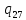 vR
vR
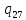 *->
*-> *R
*R
 d->
d-> dR
dR
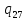 m->
m->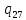 mR
mR
 ~->
~->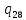 ~L
~L
//Очистка всех признаков
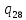 d->
d->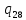 ~L
~L
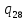 m->
m-> ~L
~L
 *->
*->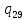 *R
*R
//Слово не принадлежит
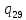 ~->
~->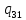 0L
0L
//Замена всех разделителей
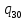 1->
1->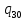 1L
1L
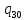 0->q300L
0->q300L
q30o-> 1L
1L
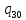 p->
p-> 0L
0L
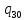 n->
n->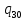 1L
1L
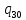 v->
v->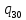 1L
1L
 u->
u-> 0L
0L
 h->
h->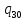 0L
0L
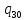 a->
a->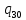 0L
0L
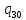 b->
b->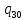 1L
1L
 ~->
~->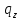 ~R
~R
//Слово принадлежит
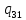 *->
*-> *L
*L
 ~->
~-> 1L
1L
Рисунок 3.1, лист 4 – Система команд МТ
3.2 Протоколы работы машины Тьюринга (на двух словах языка и двух словах, не принадлежащих языку)
Пример работы алгоритма на слове “01”, которое не является словом исходного языка приведен в таблице 3.1.
Таблица 3.1 – Протокол работы МТ на слове “01”
|
Шаг |
Состояние |
Слово на ленте |
Команда |
|
1 |
|
λ01λ |
|
|
2 |
|
λ01λ |
|
|
3 |
|
λ01λ |
|
|
4 |
|
λ0b*λ |
|
|
5 |
|
λab*λ |
|
|
6 |
|
λab*λ |
|
|
7 |
|
λab*λ |
|
|
8 |
|
λab*λ |
|
|
9 |
|
λab*λ |
|
|
10 |
|
λab*λ |
|
|
11 |
|
λab*λ |
|
|
12 |
|
λab*0 |
|
|
13 |
|
λab*0 |
|
|
14 |
|
λab*0 |
|
|
15 |
|
λa1*0 |
|
|
16 |
|
λ01*0 |
|
|
|
|
λ01*0 |
|
В таблице 3.2 представлен протокол работы машины Тьюринга на пустом слове. Это слово принадлежит языку, что совпадает с результатом работы машины.
Таблица 3.2 – Проток работы МТ на пустом слове
|
Шаг |
Состояние |
Слово на ленте |
Команда |
|
1 |
|
λλλ |
|
|
2 |
|
λ*λ |
|
|
3 |
|
λ*λ |
|
|
4 |
|
λ*λ |
|
|
5 |
|
λ*λ |
|
|
6 |
|
λ*λ |
|
|
7 |
|
λ*λ |
|
|
8 |
|
λ*λ |
|
|
9 |
|
λ*λ |
|
|
10 |
|
λ*1 |
|
|
11 |
|
λ*1 |
|
|
12 |
|
λ*1 |
|
|
13 |
|
λ*1 |
|
В таблице 3.3 представлен протокол работы распознающей машины Тьюринга на слове 1. Это слово не принадлежит языку, что сходится с результатом выполнения машины.
Таблица 3.3 – Протокол работы МТ на слове “1”
|
Шаг |
Состояние |
Слово на ленте |
Команда |
|
1 |
|
λ1λ |
|
|
2 |
|
λ1* |
|
|
Продолжение таблицы 3.3 | |||
|
3 |
|
λb* |
|
|
4 |
|
λb* |
|
|
5 |
|
λb* |
|
|
6 |
|
λb* |
|
|
7 |
|
λb*λ |
|
|
8 |
|
λb*λ |
|
|
9 |
|
λb*0 |
|
|
10 |
|
λb*0 |
|
|
11 |
|
λ1*0 |
|
|
12 |
|
λ1*0 |
|
|
13 |
|
λ1*0 |
|
Пример правильных слов алфавита более приводится не будут, так как они громоздки в просчетам, потому что график алгоритма имеет квадратичную зависимость и резкие скачки на словах, принадлежащих исходному алфавиту.
3.3 Программная модель машины Тьюринга
Для наглядной демонстрации работы детерминированной машины Тьюринга была разработана программа.
Программная модель распознающей машины Тьюринга реализована на языке программирования С#. Исходный код программы представлен в приложении Д.
Лента моделируется с помощью множества элемента управления Label, а создается в момент запуска пользователем программы. При должной настройки параметров экземпляров этого класса, получается точная графическая модель машины Тьюринга.
Все пользовательские команды загружаются сразу из файла при запуске программы, и сохраняются в специальную структура SortedList, которая обеспечивает хранение, легко обращение к командам и отсутствие дубликатов команд.
В программе предусмотрено пошаговое прохождение слова с выполнением команд, автоматическая обработка слова, построение и сохранение графика алгоритма.
3.4 Протоколы работы машины Тьюринга, построенные программно (на двух словах языка и двух словах, не принадлежащих языку)
Протоколы работы машины Тьюринга, построенные программно, приведены в приложении В. Стрелкой в них выделено положение УУ. Символом “~” обозначен пустой символ.
3.5 Расчет временной сложности (график функции временной сложности)
Данный алгоритм устроен таким образом, что наибольшее время выполняются слова длиной, кратной трем, так как для таких слов требуется наибольшее количество проверок.
Как видно из эскиза, график имеет полиномиальную зависимость 2-го порядка с неединичными коэффициентами. Также, из-за резких скачков на точках, кратных трем, можно определить, что график описывается системой из трех квадратичных уравнений.
Машина Тьюринга реализована на одной ленте, из-за чего требуются многочисленные проходы по слову для установки тех или иных разделителей.
Для слов длины кратной трем используется проход до конца слова и обратно за 2(n+2) шагов, после чего делается снова возврат на конец слова и начинается сравнение частей слов, тактами длиной (n+2)/3.
Для слов длины не кратной трем используется 2(n+2) шагов для установки разделителя, после чего осуществляется (n+2)/3 шагов для проверки слова на четность. Так как слово не принадлежит алфавиту, то делается возврат на начало слова, длиной n+2.
Таким образом, график состоит из трех частей, и экспериментально были выведены уравнения определенных точек. Уравнения приведены формулой 3.3.
(3.3)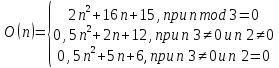
Построенный программой график практически совпадает с теоретическими расчетами. На рисунке 3.2 приведен график сложности алгоритма.
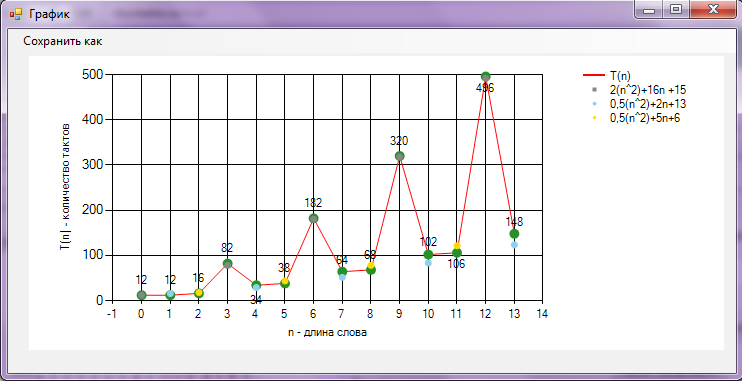
Рисунок 3.2 – График сложности алгоритма


 1
->
1
->
 1R
1R
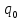 λ
->
λ
->
 *L
*L
 1
->
1
-> bL
bL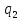
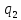 0
->
0
->
 aL
aL
 λ
->
λ
->
 λR
λR
 a
->
a
->
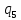 aR
aR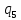
 b
->
b
->
 bR
bR
 *
->
*
->
 *R
*R
 ~
->
~
->
 ~L
~L
 *
->
*
->
 *R
*R
 ~
->
~
->
 0L
0L
 *
->
*
->
 *L
*L
 b
->
b
->
 1L
1L
 a
->
a
->
 0L
0L
 ~
->
~
->
 ~R
~R


 R
R











 1
->
1
-> bL
bL
 ->
->
 R
R
 b
->
b
->
 bR
bR
 *
->
*
->
 *R
*R
 ->
->
 L
L
 *
->
*
->
 *R
*R
 ->
->
 0L
0L
 *
->
*
->
 *L
*L
 b
->
b
->
 1L
1L
 ->
->
 R
R