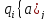- •1 Описание формальной модели алгоритма на основе рекурсивных функций
- •2 Описание аналитической модели алгоритма в виде элементарных машин тьюринга и композиции мт
- •3 Разработка аналитической и программной модели алгоритма для распознающей машины тьюринга
- •4 Разработка аналитической модели алгоритма с использованием нормальных алгоритмов маркова
- •01X110d
 МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ, МОЛОДЕЖИ И СПОРТА
УКРАИНЫ
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ, МОЛОДЕЖИ И СПОРТА
УКРАИНЫ
ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ И ИНФОРМАТИКИ
КУРСОВАЯ РАБОТА
по курсу: «Дискретные структуры»
на тему: «Построение аналитических моделей алгоритмов и оценка их сложности»
Руководитель: Выполнил:
доцент каф. ПМИ студент гр. ПС-10А
Назарова И. А. Подтынный С.Д.
__.__ . 2011 г. __ .__ . 2011 г.
Донецк 2011
 РЕФЕРАТ
РЕФЕРАТ
Отчет по курсовой работе содержит: 55 страниц, 21 рисунков, 4 таблиц, 5 приложения, 3 источника.
Объект исследования – рекурсивные функции, машины Тьюринга, нормальные алгоритмы Маркова.
Цель
– сформировать формальное определение
алгоритма в виде трех аналитических
моделей, написать программную реализацию
машины Тьюринга, распознающей язык L =
{ wwRwR│w
 {0,1}*
}, построить график временной сложности.
{0,1}*
}, построить график временной сложности.
Результат
– формальное определение алгоритмов
на основе рекурсивных функций, машин
Тьюринга и нормальных алгоритмов
Маркова, программная реализация машины
Тьюринга, распознающей язык
L = { wwRwR
│w
 {0,1}*
}, график временной сложности машины
Тьюринга, файловый вариант протокола
работы машины Тьюринга.
{0,1}*
}, график временной сложности машины
Тьюринга, файловый вариант протокола
работы машины Тьюринга.
МАШИНА ТЬЮРИНГА, ВРЕМЕННАЯ СЛОЖНОСТЬ, АЛФАВИТ, ЛЕНТА, ЯЗЫК, РАСПОЗНАВАНИЕ, АНАЛИТИЧЕСКАЯ МОДЕЛЬ, ПРИНАДЛЕЖНОСТЬ
 СОДЕРЖАНИЕ
СОДЕРЖАНИЕ
Введение..................................................................................................................4
1 Описание формальной модели алгоритма на основе рекурсивных
функций....................................................................................................................5
2 Описание аналитической модели алгоритма в виде элементарных машин
Тьюринга и композиции МТ..................................................................................8
3 Разработка аналитической и программной модели алгоритма для
распознающей машины Тьюринга.......................................................................14
3.1 Формальное определение распознающей машины Тьюринга....................14
3.2 Протоколы работы машины Тьюринга (на двух словах языка и двух
словах, не принадлежащих языку).......................................................................18
3.3 Программная модель машины Тьюринга......................................................20
3.4 Протоколы работы машины Тьюринга, построенные программно (на
двух словах языка и двух словах, не принадлежащих языку)..........................21
3.5 Расчет временной сложности (график функции временной сложности).............................................................................................................21
4 Разработка аналитической модели алгоритма с использованием
нормальных алгоритмов Маркова.......................................................................23
Выводы...................................................................................................................25
Перечень ссылок...................................................................................................26
Приложение А Техническое задание..................................................................27
Приложение Б Руководство пользователя..........................................................30
Приложение В Протоколы работы машины Тьюринга, построенные
программно............................................................................................................32
Приложение Д Исходный код программы..........................................................41
Приложение Е Экранные формы……….............................................................54
ВВЕДЕНИЕ
Первым дошедшим до нас алгоритмом в его интуитивном понимании – конечной последовательности элементарных действий, решающих поставленную задачу, считается предложенный Евклидом в III веке до нашей эры алгоритм нахождения наибольшего общего делителя двух чисел (алгоритм Евклида). В течение длительного времени, вплоть до начала XX века само слово «алгоритм» употреблялось в устойчивом сочетании «алгоритм Евклида». Для описания пошагового решения других математических задач использовалось слово «метод».
Начальной точкой отсчета современной теории алгоритмов можно считать работу немецкого математика Курта Гёделя (1931 год - теорема о неполноте символических логик), в которой было показано, что некоторые математические проблемы не могут быть решены алгоритмами из некоторого класса. Общность результата Геделя связана с тем, совпадает ли использованный им класс алгоритмов с классом всех (в интуитивном смысле) алгоритмов. Эта работа дала толчок к поиску и анализу различных формализаций алгоритма.
Первые фундаментальные работы по теории алгоритмов были опубликованы независимо в 1936 году годы Аланом Тьюрингом, Алонзо Черчем и Эмилем Постом. Предложенные ими машина Тьюринга, машина Поста и лямбда-исчисление Черча были эквивалентными формализмами алгоритма. Сформулированные ими тезисы (Поста и Черча-Тьюринга) постулировали эквивалентность предложенных ими формальных систем и интуитивного понятия алгоритма. Важным развитием этих работ стала формулировка и доказательство алгоритмически неразрешимых проблем. [1]
1 Описание формальной модели алгоритма на основе рекурсивных функций
Исторически первой алгоритмической системой была система, основанная на использовании конструктивно определяемых арифметических (целочисленных) функций, получивших специальное название рекурсивных функций. Рекурсией называется способ задания функции, при котором значение определяемой функции для произвольных значений аргументов выражается известным образом через значения определяемой функции для меньших значений аргументов [2].
Задание: разработать алгоритм функции f(n), который находит ближайшее к n простое число.
(1.1)
(1.1)
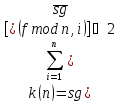
Поиск ближайшего числа состоит из трех частей: нахождения ближайшего простого, которое меньше заданного числа, нахождения ближайшего простого числа, большего заданного, и сравнения найденных чисел. Для реализации первой части поиска была выведена формула (1.2):
(1.2)

Функция нахождения ближайшего простого числа сверху описывается формулой (1.3):
(1.3)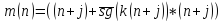
Наконец, функция, находящая ближайшее простое число к числу n приведена на рисунке 1.1:

(1.1)
(1.1)
(1.1)
(1.1)
(1.1)
(1.1)
На рисунке 1.2 приведен пример работы алгоритма в частном случае, когда n=0.
n=0
0-не простое и не составное
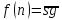 (0)=1
(0)=1
Рисунок 1.2 – Частный случай решения (n=0)
На рисунке 1.3 приведен пример работы алгоритма, когда n=1.
n=1
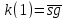 (
(
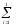 [
[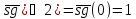 ;
;
 ;
;

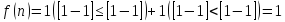
Рисунок 1.3 –Частный случай решения (n=1)
На рисунке 1.4 приведен пример работы алгоритма, если на вход подается число, которого ближайшие числа (сверху и снизу) находятся на одном и том же расстоянии от исходного числа.



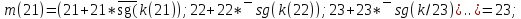

Рисунок 1.4 – Результат работы алгоритма (n=21)
Функция сравнения написана таким образом, что если расстояние до двух простых чисел одинаковое, то всегда выбирается простое, которое меньше заданного числа.
Если на вход будет подано сразу простое число, то оно и будет результатом работы алгоритма.
Полученная рекурсивная функция является примитивно-рекурсивной, потому что она получена благодаря конечному применению оператора суперпозиции и примитивной рекурсии. Функции сложения, умножения, нахождения максимума и минимума, знак, анти знак, использованные в алгоритме, являются примитивно-рекурсивными.
2 Описание аналитической модели алгоритма в виде элементарных машин тьюринга и композиции мт
Задание:
реализовать выделение подстроки,
заключенной между двумя символами
 (первая пара) в алфавите
(первая пара) в алфавите .
Если последовательность
.
Если последовательность отсутствует на ленте, стереть все.
отсутствует на ленте, стереть все.
Опишем работу машины Тьюринга тремя способами:
а) системой команд;
б) функциональной таблицей;
в) графом (диаграммой) переходов.
В таблице 2.1 представлена функциональная таблица, в которой записаны переходы между состояниями машины Тьюринга, выполняющей поставленную задачу.
Таблица 2.1 – Функциональная таблица
|
|
a |
b |
* |
0 |
1 |
= |
λ |
|
q0 |
q0aR |
q0bR |
q0*R |
- |
- |
- |
q1=L |
|
q1 |
q1aL |
q1bL |
q1*L |
- |
- |
- |
q2 λR |
|
q2 |
q2aR |
q2bR |
q3*R |
- |
- |
q8=L |
- |
|
q3 |
q40R |
q71R |
q9*L |
q3aL |
q3bL |
q8=L |
- |
|
q4 |
q4aR |
q4bR |
q5*R |
- |
- |
- |
- |
|
q5 |
q5aR |
q5bR |
q5*R |
- |
- |
q5=R |
q6aL |
|
q6 |
q6aL |
q6bL |
q6*L |
q30R |
q31R |
q6=L |
- |
|
q7 |
q7aR |
q7bR |
q7*L |
- |
- |
q7=R |
q6bL |
|
q8 |
q8aL |
q8bL |
q8*L |
- |
- |
- |
qzλR |
|
q9 |
q9aL |
q9bL |
q9*L |
q9aL |
q9bL |
- |
qzλR |
На рисунке 2.1 представлено описание машины Тьюринга с помощью системы команд.
//Установка разделителя
“=”
q0*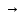 q0*R
q0*R
q0a
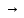 q0aR
q0aR
q0b
 q0bR
q0bR
q0λ q1=L
q1=L
//Возврат на начало
слова
q1*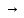 q1*L
q1*L
q1a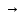 q1aL
q1aL
q1b q1bL
q1bL
q1λ q2
λR
q2
λR
//Поиск символа “*”
q2* q3*R
q3*R
q2a q2aR
q2aR
q2b q2bR
q2bR
q2= q8=L
q8=L
//Установка разделителей
для слова, между “*”
q3* q9*L
q9*L
q3a q40R
q40R
q3b q71R
q71R
q30 q3aL
q3aL
q31 q3bL
q3bL
q3= q8=L
q8=L
//Копирование, если
Первым символом оказался “a”
q4* q5*R
q5*R
q4a q4aR
q4aR
q4b q4bR
q4bR
//Установка “a” после
Символа “=”
q5a q5aR
q5aR
q5b q5bR
q5bR
q5= q5=R
q5=R
q5* q5*R
q5*R
q5= q5=R
q5=R
q5
λ q6aL
q6aL
//Возврат в состояние “q3”, для копирование следующего символа
q6* q6*L
q6*L
q6a q6aL
q6aL
q6b q6bL
q6bL
q60 q30R
q30R
q61 q31R
q31R
q6= q6=L
q6=L
//Установка “b” после символа “=”
q7*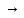 q7*R
q7*R
q7a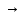 q7aR
q7aR
q7b q7bR
q7bR
q7=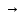 q7=R
q7=R
q7
λ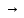 q6bL
q6bL
//Если комбинация “*…*” не найдена, возврат на начало слова
q8* q8*L
q8*L
q8a q8aL
q8aL
q8b q8bL
q8bL
q8
λ qz
λR
qz
λR
//Возврат на начало слова, и замена всех разделителей
q9* q9*L
q9*L
q9a q9aL
q9aL
q9b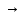 q9bL
q9bL
q91 q9bL
q9bL
q90 q9aL
q9aL
q9
λ
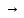 qz
λR
qz
λR
Рисунок 2.1 – Система команд
Граф переходов изображен на рисунке 2.2. Структура данного представления следующая:
- вершины графа – состояния УУ;
- дуги графа и их направление – переходы между состояниями
- вершина, из которой выходит дуга – старое состояние;
- вершина, в которую входит дуга – новое состояние;

Рисунок 2.2 – Граф состояний
Тестовый пример работы алгоритма приведен на рисунке 2.3.
Исходное слово - *ab*b
q0*ab*b
* q0ab*b
 *a
q0b*
*a
q0b*
 *ab
q0*
*ab
q0*
 *ab*
q0λ
*ab*
q0λ
 *ab*q1=
*ab*q1=
 *abq1*=
*abq1*=
 *aq1b*=
*aq1b*=
* q1ab*=
λ q1*ab*=
 q2*ab*=
q2*ab*=
 *q3ab*=
*q3ab*=
*0q4b*=
 *0bq5*=
*0bq5*=
 *0b*q5=
*0b*q5=
 *0b*=q5λ
*0b*=q5λ
 *0b*=q6a
*0b*=q6a
 *0b*q6=a
*0b*q6=a
*0bq6*=a
*0q6b*=
*0q3b*=
*01q7*=a
 *01*q7=a
*01*q7=a
 *01*=q7a
*01*=q7a
 *01*=aq7λ
*01*=aq7λ
 *01*=aq6b
*01*=aq6b
 *01*=q6ab
*01*=q6ab
 *01*q6=ab
*01*q6=ab
 *01q6*=ab
*01q6*=ab
 *01q3*=ab
*01q3*=ab
 *01q9*=ab
*01q9*=ab
 *0q9b*=ab
*0q9b*=ab
 *q9ab*=ab
*q9ab*=ab
 λq9*ab*=ab
λq9*ab*=ab
 qz*ab*=ab
qz*ab*=ab
Рисунок 2.3 – Тестовый пример работы МТ
Покажем работу машины Тьюринга на еще одном примере. На рисунке 2.4 приведен пример работы машины Тьюринга на частном случае.
Исходное слова – abba
q0abba
aq0bba
abq0ba
abbq0a
abbaq0λ
abbaq1=
abbq1a=
abq1ba=
aq1bba=
λ q1abba=
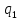 λ
abba=
λ
abba=
q2abba=
aq2bba=
abq2ba=
abbq2a=
abbaq2=
abba =
=
abb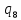 a=
a=
ab ba=
ba=
a bba=
bba=
λ
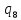 abba=
abba=
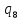 abba=
abba=
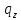 abba=
abba=
Рисунок 2.4 – Частный случай работы машины Тьюринга
Машина Тьюринга корректно отработала для двух примеров входных слов: частном и общем. Следовательно, можно полагать, что данная машина корректно отработает на всех вариантах входных слов.
Для нахождения ближайшего простого к n числа используем композицию машин Тьюринга. Для этого составим блок-схему и запишем все элементарные машины Тьюринга.
Элементарные машины Тьюринга, реализующие каждый простой блок композиции, приведены на рисунке 2.5:
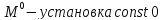
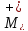 -
сумма двух аргументов
-
сумма двух аргументов
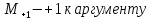
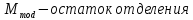
 -
предикат равенства
-
предикат равенства

 -
предикат сравнения (строгое)
-
предикат сравнения (строгое)


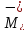 -
вычитание двух аргументов
-
вычитание двух аргументов
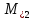 -
предикат “меньше 2” (строгое)
-
предикат “меньше 2” (строгое)
Рисунок 2.5 – Элементарный машины Тьюринга
На рисунке 2.6 приведена блок-схема алгоритма.
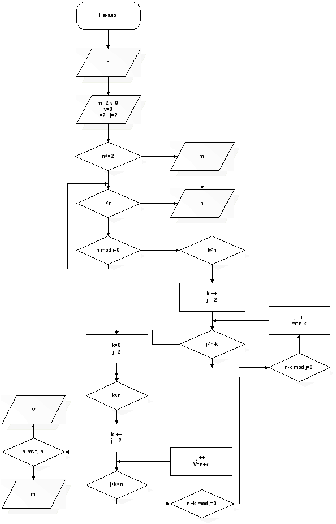 Рисунок
2.6
– Блок-схема алгоритма
Рисунок
2.6
– Блок-схема алгоритма
n*m*v*i*j*k W*n*m*v*i*j*k n
end
 *
* *
* *
* *
* *
*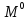


M 1
0 1 W*n*m*v*i*j*k 1
0 0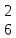

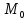
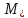 (M
(M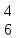 ,M
,M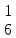 )*
)*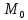
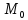
 M
M
 (M
(M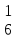 )*
)*
0 0



end W*n*m*v*i*j*k
1
0 1
β

 M
M M
M *
*


0![]()


W*n*m*v*i*j*k
 (M
(M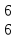 ,M
,M )*
)*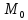


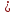


W*n*m*v*i*j*k 1 W*n*m*v*i*j*k
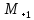 (M
(M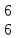 )*
)* )
)
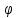
W*n*m*v*i*j*k
1
0 1
0
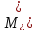 M
M ,
,
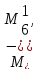 M
M *
*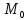


![]()


1
W*n*m*v*i*j*k
1
0 1
β 0
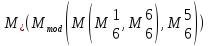

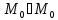



0 0



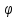
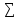
0 W*n*m*v*i*j*k


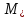 (M
(M ,M
,M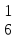 )*
)*

W*n*m*v*i*j*k 1
0 0 1
W*n*m*v*i*j*k

 (M
(M


W*n*m*v 1
1
0 ,M
,M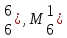
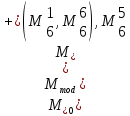

V*i*j*k

1
0 W*n*m*v V*i*j*k 0
1





1
0
0 W*n*m*v*i*j*k
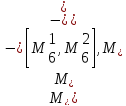 M
M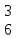 ,M
,M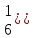


M Рисунок
2.7
– Композиция
МТ M
M