1.1.7. Прогнозування за допомогою простої лінійної регресії

Припустимо, ми хочемо одержати інформацію про можливі значення залежної змінної y₀ за умови, що незалежна змінна x приймає деяке значення x₀. Внаслідок (1.1) .Точковий прогноз знаходиться за формулою

. (1.24)

Оскільки Ea =  і Eb = , то . Отже, прогноз (1.24) є незміщеним. Дисперсіяпрогнозу (1.24) дорівнює

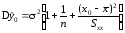. (1.25)

Для того, щоб (1.25) можна було б використовувати для інтервального оцінювання залишилось замінити дисперсію збурень на її оцінку. Позначимо

(1.26)

– стандартна похибка прогнозу. Інтервальний прогноз з рівнем довіри 1- знаходиться за наступною формулою:

,

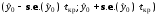де 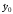– точковий прогноз (1.24), а значенняt_кр знаходиться за вибраним  в таблиці розподілу Стьюдента з n-2 ступенями свободи.

1.1.8.Приклад

В Таблиці 1.1. наведено обсяги сукупного доходу у розпорядженні та сукупного споживання для США у постійних доларах 1972 р. Дані з Таблиці 1.1. зображено графічно на на Рис.1.3. З графіка видно, що точки, які відповідають спостереженням, розташовані навколо деякої прямої, отже доцільно розглянути лінійну функцію споживання. Оцінимо її за допомогою моделі простої лінійної регресії:

y_i =  + x_i + _i ,, (1.27)

де через x_i та y_i позначено відповідно рівень доходу і споживання в році 1969 + i (наприклад i = 5 відповідає 1974 року). Спочатку обчислимо

Таблиця 1.1

Рік	Доход у розпорядженні	Особисте споживання
1970	751,6	672,1
1971	779,2	696,8
1972	810,3	737,1
1973	864,7	767,9
1974	857,5	762,8
1975	874,9	779,4
1976	906,8	823,1
1977	942,9	864,3
1978	988,8	903,2
1979	1015,7	927,6

Рис. 1.3.

=(751,6+779,2+810,3+864,7+857,5+874,9+906,8+942,9+988,8+1015,7)/10 =

= 879,24;

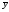=(672,1+696,8+737,1+767,9+762,8+779,4+823,1+864,3+903,2+927,6)/10 =

= 793,43;

S_xx = ((751,6 – 879,24)² + (779,2 – 879,24)² + (810,3 – 879,24)² +

+ (864,7 – 879,24)² + (857,5 – 879,24)² + (874,9 – 879,24)² +

+ (906,8 – 879,24)² + (942,9 – 879,24)² + (988,8 – 879,24)² +

+ (1015,7879,24)² ) = 67192,4;

S_yy = ((672,1 – 793,43)² + (696,8 – 793,43)² + (737,1 – 793,43)² +

+ (767,9 – 793,43)² + (762,8 – 793,43)² + (779,4 – 793,43)² +

+ (823,1 – 793,43)² + (864,3 – 793,43)² + (903,2 – 793,43)² +

+ (927,6 – 793,43)² ) = 64972,1;

S_xy = ((751,6 – 879,24) (672,1 – 793,43) + (779,2 – 879,24) (696,8 – 793,43) +

+ (810,3 – 879,24) (737,1 – 793,43) + (864,7 – 879,24) (767,9 – 793,43) +

+ (857,5 – 879,24) (762,8 – 793,43) + (874,9 – 879,24) (779,4 – 793,43) +

+ (906,8 – 879,24) (823,1 – 793,43) + (942,9 – 879,24) (864,3 – 793,43) +

+(988,8 – 879,24) (903,2 – 793,43) + (1015,7879,24) (927,6 – 793,43) ) =

= 65799,3.

За формулами (1.7) знаходими оцінки методу найменших квадратів коефіцієнгів моделі (1.27):

Отже, рівняння вибіркової регресійної прямої (рівняння фунцції споживання) має вигляд:

= – 67,58 + 0.979x. (1.28)

Рис 1.4

Графік цієї прямої зображено на Рис. 1.4. разом з фактичними даними. Щоб мати уявлення про тісноту зв’язку між доходом і споживанням, обчислимо коефі-цієнт детемінації. За формулою (1.17а) маємо: R 2 = bSxy/Syy =

= 0.97965799,3/64972,1 = 0.990702.

Як ми бачимо, зв’язок між споживанням і доходом є вельми тісним. Перед тим, як використовувати рівняння (1.28) для економічного аналізу або побудови прогнозів, модель (1.27) потрібно перевірити на адекватність. Перевіримо гіпотезу про значущість регресії двома способами. Спочатку використаємо F-статистику (1.23):

.

Нехай, рівень значущості  дорівнює 0,05. В Таблиці 3. Додатку знаходимо, що критичне значення F _кр = 5,32. Ми бачимо, що FF_кр, отже гіпотеза про рівність  нулю відхиляється, тим самим модель (1.27) є значущою.

Обчислимо стандартні похибки оцінок. Спочатку знайдемо суму квадратів залишків RSS. За формулою (1.15)

RSS = S_yy – b²S_xx = 64972,1 – 0.979²67192,4 = 537,0.

Далі знаходимо оцінку дисперсії збурень

.

Стандартна похибка b дорювнює:

SE(b) = 0.0316071.

Перевіримо гіпотезу про те, що коефіцієнт нахилу регресійної прямої  дорівнює нулю за допомогою t-статистики (1.20):

.

Нехай, рівень значущості  дорівнює 0,05. В Таблиці 1. Додатку знаходимо, що критичне значення t_кр = 2,306. Ми бачимо, що tt_кр, отже гіпотеза відхиляється.

Отже, ми можемо вважати модель адекватною (читач не повинен забувати, що повна перевірка моделі на адекватність включає аналіз залишків, з елементами якого ми ознайомимось в розділах 3 та 4).

З теорії споживання відомо, що коефіцієнт нахилу лінійної функції споживання є маргінальною або граничною схильністю до споживоння. Таким чином, ми встановили, що в середньому 0.979100 = 97,9% прирісту доходу витрачається на споживання¹⁾. Обчислене значення граничної схильності до споживання знаходиться в інтервалі (0; 1), що узгоджується з економічною теорією.

1)¹⁾ Оцінка параметра називається незміщеною, якщо .

2)²⁾ Знак «~» читається: (випадкова величина) «має розподіл».

1)¹⁾Слід зазначити, що лінійні функції споживання у вигляді (1.27) не розглядаються в серйозних дослідженнях починаючи з 50-х років, тому наведені результати мають лише учбове значення.