
Лабораторна робота №1
Тема: «Теорія множин».
Мета: вивчити основні аксіоми, закони і теореми теорії множин, навчитися застосовувати їх на практиці.
Завдання:
-
написати програму, яка буде виконувати будь-які операції над множинами (блок схеми основних операцій над множинами наведено на рисунках 1-6);
-
скласти алгоритм і написати програму, що буде обчислювати функцію множин (згідно свого варіанта, приведеного в таблиці 1);
-
виконати спрощення заданної формули та порівняти результати.
Теоретичні основи:
Множина – усяка сукупність визначених елементів, які можуть бути зв'язаними між собою за допомогою деякої властивості.
Множини позначаються великими латинськими буквами. Об'єкти, що складають множини, називаються елементами і позначаються малими буквами латинського алфавіту.
Кінцева множина – це така множина, кількість елементів якої може бути виражена кінцевим числом, причому не важливо, чи можемо ми порахувати це число в даний момент.
Нескінченна множина - це така множина, що не є кінцевою.
Множина може задаватися у кілька способів.
Кінцеву множину можливо задати переліком її елементів.
Нескінченну множину можливо задати вказівкою характерної властивості.
Приклад
A={x: x*x-1=0}
B={x1,x2,x3,x4}
Основні аксіоми теорії множин:
-
Аксіома існування – завжди існує хоча б одна множина;
-
Аксіома еквівалентності – якщо множини А та В складаються з тих самих елементів;
-
Аксіома об'єднання – для двох довільних множин А та В існує множина С, елементами якої є кожен елемент, що утримується в одній з цих двох множин або в обох одночасно;
-
Аксіома перетинання – для двох довільних множин А та В існує множина С, елементами якої є кожен елемент, що одночасно належить і множині А і множині В;
-
Аксіома про універсальну множину – для довільної групи множин Ai-тих завжди існує множина I, для якої виконується співвідношення Ai
 I
I -
Аксіома про порожню множину – завжди існує множина, якій не належить жоден елемент.
Виходячи з основних аксіом, визначені додаткові операції над множинами:
-
Доповнення множини – для довільної множини М існує доповнення до універсальної множини і позначається це доповнення М :
М М=I
М=I
M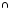 M=Ǿ
M=Ǿ
-
Різниця між множинами – для довільної множини А и В існує множина С , яка включає такі елементи першої множини, які не співпадають з елементами другої множини:
С=А\В=А
 В
В
С=В\А=В
 А
А
-
Симетрична різниця між множинами –
С=АΔВ=
А\В
 В\А
В\А
Основні закони операцій перетинання й об'єднання
-
Закон комутатівності-
А В=В
В=В
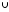 А;
А
А;
А В=В
В=В А
А
-
Закон асоціативності
(А В)
В)
 С=А
С=А
 (B
(B
 С)
С)
(А В)
В)
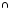 C=А
C=А
 (B
(B
 С)
С)
-
Закони дистрибутивності:
1-ий
– (А В)
В)
 C=(А
C=(А C)
C)
 (B
(B C)
C)
2-ий
- (А В)
В)
 C=(А
C=(А C)
C)
 (B
(B C)
C)
-
Закони де Моргана.


А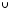 В= А
В= А В А
В А В= А
В= А В
В
Приклади деяких операцій над множинами.
Довести тотожності.
-
А\(B
 C)=(А\B)
C)=(А\B)
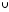 (А\C)
(А\C)
(А В)
В)
 (А
(А C)=А\(B
C)=А\(B C)-
доведено
C)-
доведено
-
А\(А\B)=А
 В
В
А\(А В)=А
В)=А (А
(А В)=А
В)=А (А
(А В)=А
В)=А А
А А
А В=А
В=А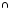 В-доведено
В-доведено
3. А В=А
В=А (B\А)
(B\А)
А (В
(В А)=А
А)=А В
В А
А А=А
А=А В
В I=А
I=А В-доведено
В-доведено
