
- •Методические указания и задания
- •Содержание
- •Теоретические вопросы по модулю 2 «Графы»………………………….41 Список рекомендуемой литературы……………………………………..41 Введение
- •Лабораторная работа №1
- •Теоретические сведения
- •Задание 1
- •Задание 2
- •Задание 3
- •Контрольные вопросы
- •Лабораторная работа №2
- •Теоретические сведения:
- •Задание 1
- •Задание 2.
- •Задание 3.
- •Контрольные вопросы:
- •Лабораторная работа №3
- •Теоретические сведения
- •Задание 1.
- •Задание 2.
- •Контрольные вопросы
- •Лабораторная работа №4
- •Теоретические сведения
- •Соединения с повторениями.
- •Задание 1.
- •Задание 2.
- •Контрольные вопросы
- •Теоретические вопросы по первому модулю
- •Лабораторная работа №5
- •Теоретические сведения
- •Варианты заданий к лабораторной работе № 4
- •Контрольные вопросы
- •Лабораторная работа №6
- •Теоретические сведения
- •Варианты заданий к лабораторной работе №5
- •Контрольные вопросы
- •Теоретические вопросы по модулю 2 «Графы»
- •Рекомендуемая литература
Учебное издание
Методические указания и задания
к лабораторным работам
по курсу
"ДИСКРЕТНАЯ МАТЕМАТИКА"
для студентов специальностей
7.091501: "Компьютерные системы и сети"
7.091502: ”Системное программирование”
направления подготовки 0915 «Компьютерная инженерия»
Составитель: Чередникова О.Ю.,
доцент кафедры «Компьютерная инженерия»
Донецк 2013
УДК 681.973
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ ПО КУРСУ «ДИСКРЕТНАЯ МАТЕМАТИКА» (для студентов направления подготовки 6.0915 «Комп'ютерна інженерія», специальностей 7.091501 - "Компьютерные системы и сети" и 7.091502 - "Системное программирование").
Составитель: Чередникова О.Ю. – Донецк: ДВНЗ «Донецкий национальный технический университет», 2013 г. – 42 с.
Целью методических указаний по курсу «Дискретная математика» является приобретение студентами практических навыков решения задач теории множеств и теории графов, в частности, доказательства тождеств с помощью законов алгебры множеств, решение комбинаторных задач и задач, решаемых с помощью графов.
Методические указания содержат варианты заданий, примеры выполнения лабораторных работ, а также необходимый пояснительный материал.
Составитель:
к.т.н., доцент каф. КИ Чередникова О.Ю.
Ответственный за выпуск:
д.т.н., профессор Святный В.А.
Рецензенты:
к.т.н., доцент каф. КИ нокутский В.А.
к.т.н., доцент каф. АСУ Фонотов А.М.
Содержание
Введение……………………………………………………………………..6
Лабораторная работа №1…………………………………………………7
Лабораторная работа №2…………………………………………………14
Лабораторная работа №3…………………………………………………23
Лабораторная работа №4…………………………………………………27
Теоретические вопросы по модулю 1 «Теория множеств»……………32
Лабораторная работа №5…………………………………………………33
Лабораторная работа №6…………………………………………………38
Теоретические вопросы по модулю 2 «Графы»………………………….41 Список рекомендуемой литературы……………………………………..41 Введение
Целью лабораторных работ по курсу «Дискретная математика» является приобретение студентами практических навыков решения задач теории множеств и теории графов. Данные методические указания предназначены для студентов, обучающихся по направлению подготовки «Компьютерная инженерия» специальностей «Компьютерные системы и сети» и «Системное программирование».
Материал, излагаемый в методических указаниям, содержит теоретические сведения по вопросам доказательства тождеств с помощью законов алгебры множеств, изучения свойств отношений и, в частности, функциональных отношений, решения комбинаторных задач, а также задач теории графов.
С целью закрепления материала предлагаются варианты для индивидуального выполнения задания студентами. Материал разбит на две части – два модуля: теория множеств и теория графов. В конце каждой части находятся вопросы для проверки знаний по соответствующему модулю.
Лабораторная работа №1
Цель: Освоить основные операции над множествами.
Тема: Операции над множествами
Задание 1Задание 2Задание 3
Теоретические сведения
Понятию множества нельзя дать строгого определения. Более общего понятия, чем множество в математике не существует. Это - "совокупность, собрание, класс, семейство". Часто множество - несколько объектов, объединенных общим признаком.
Предметы, составляющие множество, называются элементами. Для указания того, что множество А состоит из элементов х, у ...z пишут А={ х,у.... }. Например: множество арифметических действий состоит из элементов { сложения, вычитания, умножения, деления }. Tо, что элемент хпринадлежитмножеству А, записывают xA. Если не принадлежитxA.
Например: если А - множество натуральных чисел, то 6 А, а вот 1.3А.
Операции над множествами
Объединением (суммой)множеств А и В называется множество, каждый элемент которого принадлежит хотя бы одному из множеств А и В. (Обозначение АВ={x x Aили x B})
Пусть А={ 1,2,3 }; В={ 1,2,4,5 }; A В={ 1,2,3,4,5 }.

Пересечением (произведением)множеств А и В называется множество, каждый элемент которого принадлежит одновременно А и В (обозначается АВ={x x Aи x B}).
П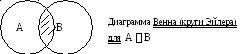 усть
А={ 1,2,3 }; B={1,2,4,5}; АВ={ 1,2 }.
усть
А={ 1,2,3 }; B={1,2,4,5}; АВ={ 1,2 }.
Разностьюдвух множеств А и В (относительным дополнением), называется новое множество А-В или А/В в которое входят все элементы множества А не принадлежащие В.A - B = {x xAи xB}. Совсем не обязательно, чтобы множество А было частью множества В.
П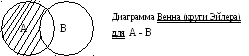 ример:
A={1,2,3,4} B={1,3,5} A-B={2,4} B-A={5}
ример:
A={1,2,3,4} B={1,3,5} A-B={2,4} B-A={5}
Симметрической разностьюдвух множеств А и В, называется новое множество АΔВ, в которое входят все элементы множества А-В и В-А.
AΔB = {x (xAи xB)или(xВи xА) }.
П ример:A={1,2,3,4}B={1,3,5}AΔB={2,4,5}
ример:A={1,2,3,4}B={1,3,5}AΔB={2,4,5}
