Группа иус 13зуск

1. Проверка арифметического выражения на корректность. Арифметическое выражение может включать знаки математических операций (+, -, *, /, =), имена переменных (начинается с буквы) и числовые константы.

2. Необходимо подсчитать, сколько слов и десятичных чисел содержится в тексте.

3. Проверка правильности записи римских чисел. (Римские числа записываются символами I-1, V-5, X-10, L-50, C-100, D-500, M-1000. Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц. При этом некоторые из цифр (I, X, C, M) могут повторяться, но не более трех раз, таким образом с их помощью можно записать любое целое число не более 3999. Например, 283  CCLXXXIII, то есть 200+50+30+3=283. Здесь цифра, изображающая сотню, повторена два раза, а цифры, изображающие соответственно десяток и единицу, повторены по три раза. Меньшая цифра может быть записана и слева от большей, тогда ее следует вычесть из большей. В этом случае повторения меньшей цифры не допускаются: 94 XCIV=100-10+5-1=94).

4. На ленте машины Тьюринга находится десятичное число. Определите, делится ли это число на 4 без остатка. Если делится, то запишите справа от числа слово «да», если нет — «нет». Каретка находится где-то над числом.

5. Поиск двоичных чисел в тексте и вычисление их суммы.

6. На вход считывающего устройства посимвольно подаются положительные и отрицательные целые десятичные числа. Необходимо сохранить значение числа или выдать сообщение об ошибке, если число записано неверно.

7. В тексте заменить операторные скобки begin end фигурными { }.

8. Слово Р имеет следующий вид: 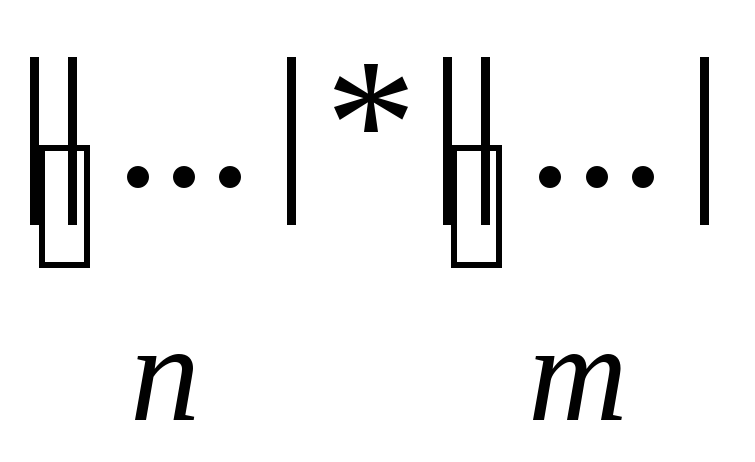. Реализовать операцию умножения в единичной системе счисления (в качестве ответа выдать слово справа от стрелки):

9. A={0,1,2,3}. Считая непустое слово P записью числа в четверичной системе счисления, получить запись этого числа в двоичной системе.

10. Проверка соответствия закрывающих и открывающих скобок в тексте программы.

11. Пусть P имеет вид Q–R, где Q и R – непустые слова из символов 0, 1 и 2. Трактуя Q и R как записи чисел в троичной системе счисления (возможно, с незначащими нулями) и считая, что Q≥R, выдать в качестве ответа запись разности этих чисел в той же троичной системе.

12. А={|} . Считая слово Р записью числа в единичной системе счисления, определить, является ли это число степенью 3 (1, 3, 9, 27, …). Ответ: пустое слово, если не является, или слово, состоящее из количества палочек, равного степени в противном случае.

13. На вход считывающего устройства посимвольно подается двоичное число в виде (например) 101.11. Необходимо сохранить значение этого числа в десятичном виде или выдать сообщение об ошибке, если число записано неверно.

14. Дан массив из открывающихся и закрывающихся скобок. Постройте машину Тьюринга, которая удаляла бы пары взаимных скобок. Например, дано: « ) ( ( ) ( ( ) », надо получить: «)…( ( ».

15. Дана строка из букв а и b. Разработайте машину Тьюринга, которая переместит все буквы а в левую, а буквы b в правую часть строки. Каретка находится над крайним левым символом строки.

16. Даны два целых положительных числа в различных системах счисления, одно — в троичной системе, другое — в десятичной. Разработайте машину Тьюринга, которая будет находить сумму этих чисел в десятичной системе счисления.

17. На ленте машины Тьюринга находится десятичное число. Определите, делится ли это число на 3 без остатка. Если делится, то запишите справа от числа слово «да», если нет — «нет». Каретка находится где-то над числом.

18. Постройте машину Тьюринга (называемую «транспозиция» и обозначаемую В), которая перерабатывает слово 01y01x0 в слово 01x01y0, причем в начальном и конечном положении обозревается ячейка, содержащая 0, между двумя наборами единиц.

19. На ленте машины Тьюринга записано число в десятичной системе счисления. Каретка находится над крайней правой цифрой. Запишите цифры этого числа в обратном порядке.

20. Слово Р имеет следующий вид: 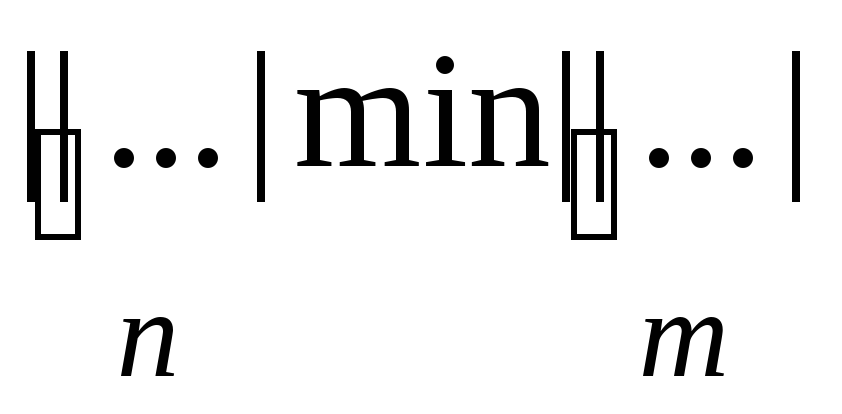. Реализовать операцию определения минимального из чисел в единичной системе счисления (в качестве ответа выдать слово справа от стрелки):

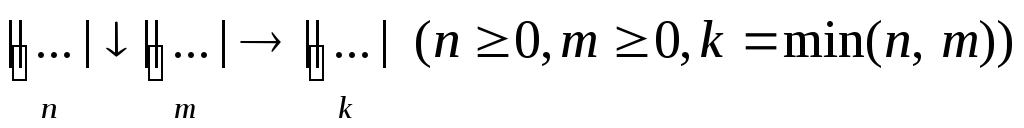
21. Подсчитать количество буквосочетаний «кар» и «рак» во входном тексте. Считаем, что их не может быть больше 15.

22. A={М,С,X,L}. Определить, является ли непустое слово правильной записью римского числа.