4) Изучение основной тенденции способом аналитического выравнивания ряда динамики

Сущность способа заключается в том, что, исходя из предположения о той или иной закономерности роста или снижения уровней, выбирается форма аналитического выражения тренда (вид аппроксимирующей функции).

Вид аппроксимирующей функции (уравнения тренда)выбирается на основании:

а) анализа простейших показателей динамики;

б) в результате применения способа укрупнения интервала;

в) в результате применения способа скользящей средней.

Выбранная функция выражает предполагаемую закономерность плавного изменения уровня во времени, т.е. тренд.

При этом каждый уровень ряда рассматривается как сумма двух компонентов:

, (1.19)

где - трендовая компонента, характеризующая влияние постоянно действующих основных факторов;

- случайная (остаточная) компонента (отражает влияние случайных факторов и обстоятельств);

y_t – уровень ряда динамики.

Чаще всего в качестве уравнения тренда используют :

1) - уравнение прямой линии;

2) - уравнение показательной функции;

3) - уравнение параболы второго порядка,

где a₀ , a₁, a₂ –параметры уравнения тренда.

После выбора уравнения тренда вычисляются его параметры.

Для уравнения прямой линии параметры можно определить по следующим формулам:

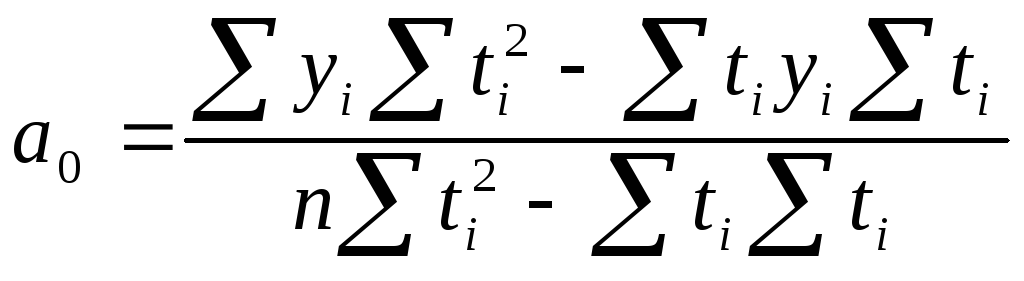,(1.20)

,(1.21)

где n — число моментов времени, для которых были получены исходные уровни ряда .

Если вместо абсолютного времени выбрать условное время таким образом, чтобы, то записанные выражения для определенияупрощаются:

;(1.22)

.(1.23)

При выборе условного времени необходимо исходить из того, что интервалы построенного таким образом ряда должны быть одинаковыми.

Пример. Выбор условного времени для ряда динамики имеющего:

- четное число уровней: - нечетное число уровней:

год	yt	ti		год	yt	ti
2000	350	- 3		2000	350	- 2
2001	320	- 1		2001	320	- 1
2002	390	+ 1		2002	390	0
2003	370	+ 3		2003	370	+ 1
Итого:	1430	0		2004	410	+ 2
				Итого	1840	0

4. Анализ колебаний и стабильности рядов динамики

4.1 Показатели вариации уровней ряда динамики относительно тренда

Для измерения колебаний уровней динамического ряда относительно тренда используют следующие показатели вариации:

- размах вариации:

; (1.24)

, (1.25)

где - трендовая компонента;

- среднее линейное отклонение:

; (1.26)

- среднеквадратическое отклонение:

; (1.27)

- относительный коэффициент вариации:

;

. (1.28)

Противоположное колеблемости свойство называется стабильностью. Количественно стабильность характеризуется коэффициентом стабильности, который определяется по следующей формуле:

. (1.29)

Чем ближе коэффициент стабильности к 1, тем больше стабильность динамического ряда.