2. Показатели анализа рядов динамики

Существуют две группы показателей анализа рядов динамики:

- простейшие показатели;

- средние показатели.

К простейшим показателям относятся:

• абсолютный прирост;

• темп роста;

• темп прироста;

• абсолютное значение (содержание) одного процента прироста.

Расчет простейших показателей основан на сравнении между собой уровней ряда динамики.

Уровень, с которым производится сравнение, называется базисным (y₀).В качестве базисного уровня чаще всего принимают первый уровень ряда (y₁) или предыдущий уровень (y_i-1).

Если все уровни сравнивают с первым уровнем y₁, то полученные показатели будут называтьсябазисными;если с предыдущимy_i-1-цепными.

Абсолютный приростпоказывает, на сколько единиц увеличился или снизился уровень, по сравнению с базисным уровнем:

;

;

. (1.1)

Абсолютный прирост за единицу времени характеризует (измеряет) абсолютную скорость роста или снижения уровня.

Базисный абсолютный прирост для всего ряда связан с цепными абсолютными приростами следующим образом:

, (1.2)

где n – число уровней ряда динамики.

Темп роста характеризует относительную скорость (интенсивность процесса) роста или снижения уровня.

Темп роста показывает во сколько раз увеличился уровень, по сравнению с базисным, а в случае уменьшения – какую часть базисного уровня составляет сравниваемый уровень:

. (1.3)

Между базисным темпом роста и цепными темпами роста существует следующая зависимость:

. (1.4)

Темп прироста характеризует относительную величину абсолютного прироста, т.е. его величину по отношению к базисному уровню:

;

. (1.5)

Абсолютное значение одного процента прироста:

. (1.6)

К группе средних показателейанализа рядов динамики относятся:

• средний уровень (хронологическая средняя);

• средний абсолютный прирост;

• средний темп роста;

• средний темп прироста.

Средние показатели применяются для обобщающей характеристики развития явления, а также для выявления и измерения основной тенденции развития явления.

Средний уровень ряда, представляет собой среднюю, рассчитанную из значений изменяющихся во времени уровней ряда.

Расчет среднего уровня ряда производится по формулам:

- для интервального ряда с равными периодами (интервалами времени):

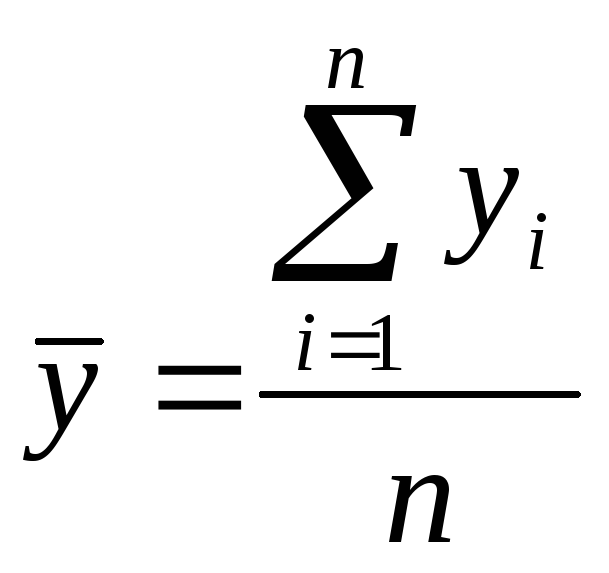. (1.7)

- для моментного рядас не равными интервалами между датами:

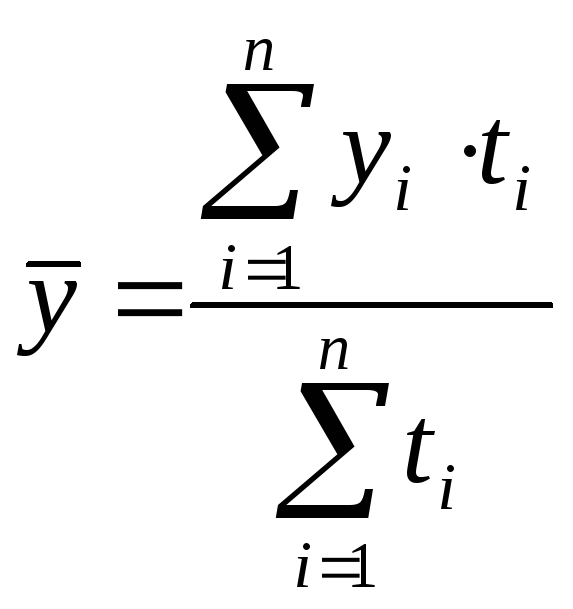. (1.8)

- для моментного рядас равными интервалами между датами:

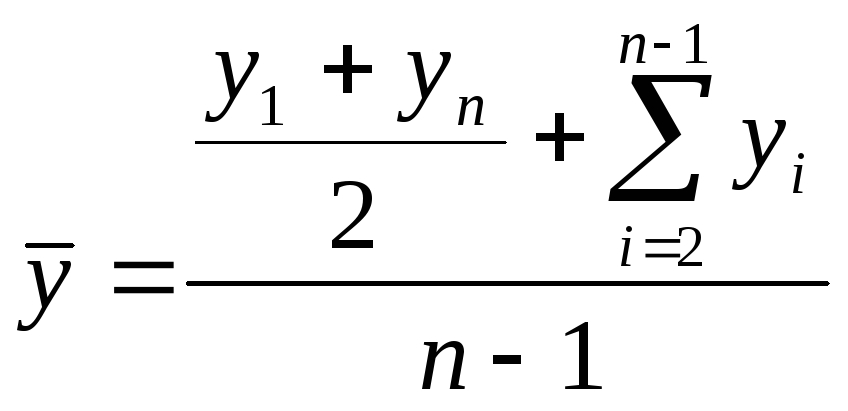. (1.9)

Средний абсолютный прирост– показывает, насколько единиц увеличивался или уменьшался уровень, по сравнению с предыдущим в среднем за единицу времени.

Средний абсолютный прирост характеризует среднюю абсолютную скорость роста или снижения уровня и всегда является интервальным показателем

;

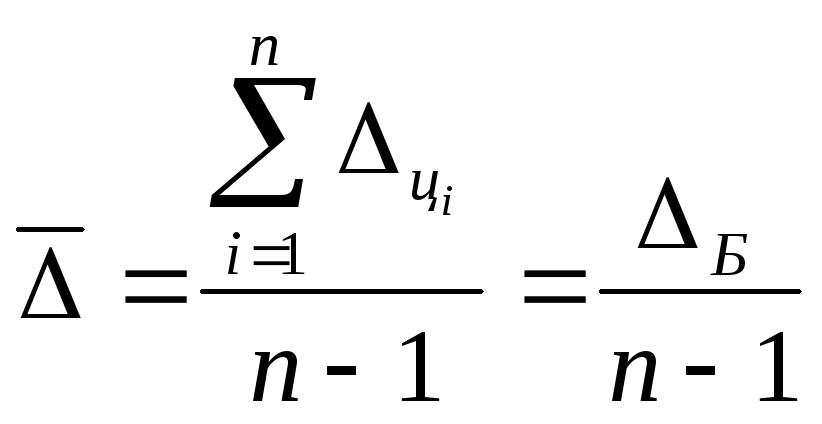. (1.10)

Средний темп роста,выраженный в форме коэффициента, показывает, во сколько раз увеличивался уровень по сравнению с предыдущим в среднем за единицу времени:

;

. (1.11)

Средний темп прироста (снижения)выраженный в процентах, показывает, насколько процентов увеличится или уменьшится уровень по сравнению с предыдущим в среднем за единицу времени.

Характеризует среднюю относительную скорость изменения уровня:

;

. (1.12)