4. Эквивалентность машин Тьюринга и частично- рекурсивных функций

Эквивалентность МТ и частично-рекурсивных функций означает, что всякая частично-рекурсивная функция оказывается вычислимой по Тьюрингу и наоборот. Приведем примеры реализации на машинах Тьюринга операторов примитивной рекурсии и минимизации.

Пример 6. Построить композицию МТ, вычисляющую в унарном коде функцию, заданную схемой примитивной рекурсии :

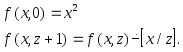
и

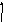
и

л

л

Здесь - копирует исходные данные и ставит маркеры «»;

- вычисляет функцию ;

- вычисляет предикат z=0;

- увеличивает i на 1 слева от первого маркера «»;

- вычисляет предикат i = z;

- вычисляет функцию

- вычисляет функцию ;

- стирает все на ленте слева от второго маркера «» включительно.

Пример 7. Построить композицию МТ, вычисляющую в унарном коде функцию, заданную оператором минимизации :

Композиция МТ имеет следующий вид :

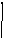
Здесь - ставит * после ;

- копирует для вычисления ;

- вычисляет ;

- вычисляет предикат (x+y)z=100 без восстановления;

- увеличивает y на 1;

- вычисляет z + y;

- стирает все непустые символы на ленте кроме .

Доказательство того, что всякая функция, вычислимая по Тьюрингу, является частично-рекурсивной, проводится в несколько этапов :

- арифметизация МТ, т.е. сведение символьных данных и операций над строками к целым неотрицательным числам и арифметическим операциям над ними ;

- доказательство примитивной рекурсивности операций, выполняемых в одном такте работы МТ;

- доказательство примитивной рекурсивности общего поведения машины ( перехода i-го такта к (i+1)-му;

- доказательство частичной рекурсивности конечного результата работы МТ.

Лекция 4. НОРМАЛЬНЫЕ АЛГОРИТМЫ МАРКОВА

Нормальные алгоритмы были предложены в 1951 г. советским ученым А.А. Марковым. Как и машины Тьюринга, нормальные алгоритмы оперируют со словами в некотором алфавите. Главное же их отличие от МТ состоит в том, что нормальный алгоритм представляет собой не устройство, а некоторый упорядоченный набор элементарных операций над словами. Операндами этих операций в общем случае являются последовательности букв, что зачастую упрощает построение нормального алгоритма по сравнению с МТ.

Для изучения данной темы необходимо повторить понятия и определения символьных конструкций и операций над ними (см. Раздел 3.1.).

В литературе алгоритмы Маркова коротко описаны в работах /1,2,5/.

1. Определение и функционирование нормального алгоритма

Вначале рассмотрим понятие марковской подстановки.

Марковской подстановкой называется операция над словами ,, заключающаяся в следующем. В исходном слове  ищется самое левое вхождение слова , и если оно существует,  заменяется на  в слове . Полученное слово ’ является результатом применения марковской подстановки к слову . Если слово  не входит в слово , то говорят, что данная марковская подстановка неприменима к слову .

Марковская подстановка обычно записывается следующим образом :



Подчеркнем, что длины слов  и  могут в общем случае не совпадать. При этом длина ’ будет отлична от длины слова . В частном случае длина слова  или слова  ( или обоих ) может быть равна нулю, соответствующее слово является пустым. В марковских подстановках пустое слово никак не обозначается и не занимает никакого места ( в отличие от машин Тьюринга, где пустой символ занимает ячейку на ленте и обозначается буквой  ). В любом слове  имеется несколько вхождений пустого слова : перед первой буквой, после последней и между каждой парой букв внутри слова. Так, в слове abcd имеется 5 вхождений пустого слова.

Если в марковской подстановке  слово  - пустое ( подстановка записывается ), то слово  приписывается слева к слову . Если пустым является  (записывается  ), то слово  исключается из  ( при этом пробелы не ставятся).

Пример 1. Рассмотрим результаты применения нескольких подстановок.

Слово  Подстановка Слово ’

1111 10 0111

космонавт навтс космос

авссваавс ссв аввваавс

аллгоритм л алгоритм

zxyz zxyz

54321 76 7654321

01011  01011

alpha xy подстановка неприменима

Заключительной называется подстановка вида



Записью (схемой) нормального алгоритма в алфавите А называется упорядоченная последовательность ( столбец ) марковских подстановок  и (или) , где  и  являются словами в А , а символы  и  не принадлежат А.

Выполнение нормального алгоритма происходит следующим образом :

1. N:=1 ( номер подстановки в схеме );

2. Выбирается N-я подстановка;

3. Левая часть подстановки  ищется в преобразуемом слове;

4. Если  найдено, то переход к пункту 7, иначе к пункту 5;

5. N:=N+1;

6. Если N не превышает общего числа подстановок, то переход к пункту 2, иначе конец;

7. Выполняется замена  на  в преобразуемом слове;

8. Если выполненная подстановка является заключительной, то конец , иначе – переход к пункту 1.

Следует подчеркнуть два момента в работе марковского алгоритма :

• после выполнения подстановки очередной шаг заключается не в выборе следующей подстановки и не в просмотре сначала преобразуемого слова, а в выборе первой подстановки в схеме, т.е. каждый раз просмотр столбца подстановок начинается сначала;

• окончание работы алгоритма может произойти в одном из двух случаев : выполнена заключительная подстановка или ни одна из подстановок неприменима.

Теперь рассмотрим основное понятие - нормальный алгоритм над алфавитом А.

Пусть некоторый алфавит В является расширением алфавита А : Тогда нормальный алгоритм в В , который слова в А , если он к ним применим, перерабатывает в результаты, являющиеся словами в А, называется нормальным алгоритмом над алфавитом А.

Другими словами, если нормальный алгоритм в А может использовать только буквы алфавита А, то нормальный алгоритм над А для преобразования слов в алфавите А может использовать вспомогательные символы. Вспомогательные символы не должны присутствовать в результирующем слове. Нормальные алгоритмы над А являются более мощными, чем алгоритмы в А.

Одноместная частичная словарная функция , заданная в алфавите А, называется нормально вычислимой, если существует нормальный алгоритм над алфавитом А, перерабатывающий слово  в слово .

Соответствие между нормальными алгоритмами над алфавитом А и алгоритмами в интуитивном смысле выражает принцип нормализации – аналог тезисов Черча и Тьюринга :

Каков бы ни был алгоритм, для которого допустимыми исходными данными и результатами являются слова в некотором алфавите, существует эквивалентный ему нормальный алгоритм в этом алфавите. Напомним, что к словам в некотором алфавите относятся также и числа в различных системах счисления.

Так же, как и тезисы Черча и Тьюринга, принцип нормализации недоказуем.