-
Композиция машины Тьюринга
Вышеперечисленные способы описания МТ практически можно использовать только для несложных алгоритмов, т.к. для сложных описание становится слишком громоздким. Точно так же описание рекурсивных функций только с помощью простейших функций и операторов суперпозиции, примитивной рекурсии и минимизации было бы чрезвычайно громоздким. Поэтому примитивная или частичная рекурсивность функции доказывается с использованием других функций, примитивная или частичная рекурсивность которых уже доказана.
Аналогично этому, машины Тьюринга для сложных алгоритмов могут строиться с использованием уже имеющихся МТ. Такое построение называется композицией МТ.
Опишем 4 основных способа композиции МТ :
- последовательная композиция ( суперпозиция );
- параллельная композиция;
- разветвление
- цикл
Последовательной
композицией машин
и
, вычисляющих словарные функции
и
в алфавите А
,
называется машина Т
, вычисляющая функцию
.
Последовательная композиция изображается
следующим образом :
T1 T2 
и
обозначается
.
Последовательная композиция используется обычно для описания линейных участков алгоритмов.
Доказательство
теоремы о возможности построения машины
T
, являющейся последовательной композицией
двух произвольных машин
и
осуществляется путем отождествления
заключительного состояния
с начальным состоянием
.
Пример
3. Построить
алгоритм умножения 2*Х в унарном коде с
использованием машины копирования
,
переводящей слово
в слово *
и машины сложения
.
Искомая МТ выглядит следующим образом
:
Параллельной
композицией машин
и
, вычисляющих словарные функции
и
в
алфавитах А
и
В
соответственно,
называется машина Т
,
вычисляющая словарную функцию
.
Здесь знак
используется для разделения слов при
параллельной композиции МТ.
Т 
и
изображается следующим образом :
и
обозначается :
.
Фактически параллельная композиция двух МТ получает на вход слово, состоящее из 2-х слов в разных алфавитах и на выходе выдает слово , состоящее из 2-х слов , т.е. представляет собой две одновременно и независимо работающие машины.
Для
реализации параллельной композиции
используется машина с двухэтажной
лентой. Необходимость в этом вызвана
тем, что вычисление
и
во
времени происходит последовательно, и
, вычисленная , например, первой, может
потребовать больше места, чем ,
и испортить слово .
Машина с двухэтажной лентой работает
следующим образом : слово
переписывается на второй этаж и стирается
на первом, вычисляется
на первом этаже, вычисляется
на втором этаже и затем переписывается
на первый этаж, возможно, со сдвигом.
Для реализации параллельной композиции n машин используется n–этажная лента.
Команда
МТ с двухэтажной лентой записывается
следующим образом :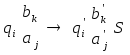
,
где
- буквы, записанные соответственно на
первом и втором этажах.
Пример
4.
Реализовать параллельную композицию
машин
и
,
вычисляющих функции
в двоичной системе счисления и a
+ b
в
унарной системе.
Входное
слово имеет вид :
.
Опишем работу МТ системой команд :
Движение
вправо до слова
Перезапись
слова
на второй этаж
Движение влево до слова
Прибавление
1 к числу Х.
Движение вправо к слову .
Перепись
на 1-й этаж с одновременным 
сложением
чисел a
и
b
.
Стирание
младшей 1 в слове .
В данном примере реализацию композиции можно было бы осуществить и с одноэтажной лентой, но он служит также для иллюстрации способа построения МТ с двухэтажной лентой.
На конкретных примерах входных данных самостоятельно покажите функционирование описанной МТ в виде последовательности конфигураций.
Разветвление
в
композиции МТ. Если заданы машины
и
,
вычисляющие словарные функции
и
,
и машина
,
вычисляющая некоторый предикат P()
с восстановлением ( т.е. без стирания
слова
) , то
для реализации разветвления может быть
построена машина Т
,
вычисляющая функцию :
Разветвление машин Тьюринга на схемах композиции изображается следующим образом :
=’и’
=’л’
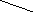
и
обозначается
,
Здесь
- результат работы машины
,
принимающий значения «и» (истина) и «л»
(ложь).
Машина
Т
представляет
собой последовательную композицию
машин
и
; система команд машины
имеет вид :
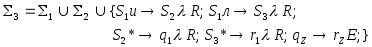
где
- начальные состояния машин
соответственно. Команды в фигурных
скобках, добавленные к системе команд
и
,
как раз и реализуют передачу управления
одной из машин
,
по результату работы машины
.
Цикл в композиции МТ реализуется по тем же принципам что и разветвление. Циклическим будем считать следующий алгоритм :
« пока
P()=’ истина ’,
выполнять
»,
где
- слово на ленте перед первым выполнением
Т
и после очередного выполнения Т.
Для реализации такого цикла используется следующая схема :
=’л’
=’и’
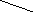
Машина
выделяет
из слова
слово ,
которое является результатом работы
всей композиции при =л.
Пример 5. Построить композицию МТ для реализации алгоритма умножения двух чисел x и y , заданных в унарном коде.
Для построения композиции вначале составим блок-схему алгоритма (рис 3.2.).
=’л’
=’и’
Рис
3.3 Композиция МТ, вычисляющая
Здесь
- вычисляет с восстановлением предикат
;
- стирает все непустые символы на ленте
( Z=0);
- выполняет операцию сложения Z+X
в унарном коде;
- уменьшает Y
на
1 ( стирает самый левый символ 1);
- конечное состояние всей МТ.
Следует отметить, что во всех случаях в начале алгоритма нужно вставлять проверку исходных данных на особые значения ( чаще всего на 0 ), несоблюдение этого требования может привести к зацикливанию.
Композиция МТ может применяться для построения сложных алгоритмов. Возникает вопрос : всякий ли алгоритм можно реализовать в виде композиции МТ ? Ответ на этот вопрос дает Тезис Тьюринга , аналог тезиса Черча : всякий алгоритм может быть реализован с помощью машин Тьюринга и наоборот, всякий процесс, реализуемый машиной Тьюринга, является алгоритмом.
Тезис Тьюринга не является теоремой, доказать его невозможно, т.к. он содержит неформальное понятие « алгоритм ». Однако многолетняя математическая практика является надежным подтверждением этого тезиса : за 50 лет не было найдено алгоритма в интуитивном смысле, который нельзя было бы реализовать с помощью машин Тьюринга.