Лабораторная работа № 2.

Тема. Действия над векторами и матрицами.

Цель работы: практика в использовании возможностей АЯ для действий над массивами.

Задача.

1. Получить элементы квадратной матрицы 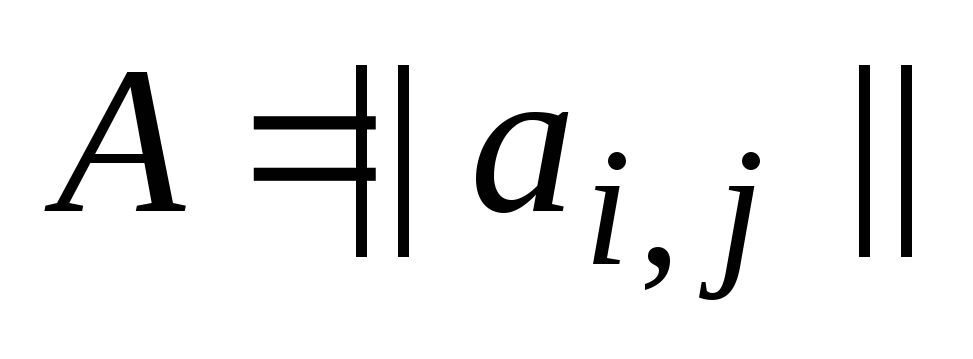размерностью не менее чемпо заданной формуле.

2. Из полученной матрицы по заданному правилу получить компоненты вектора

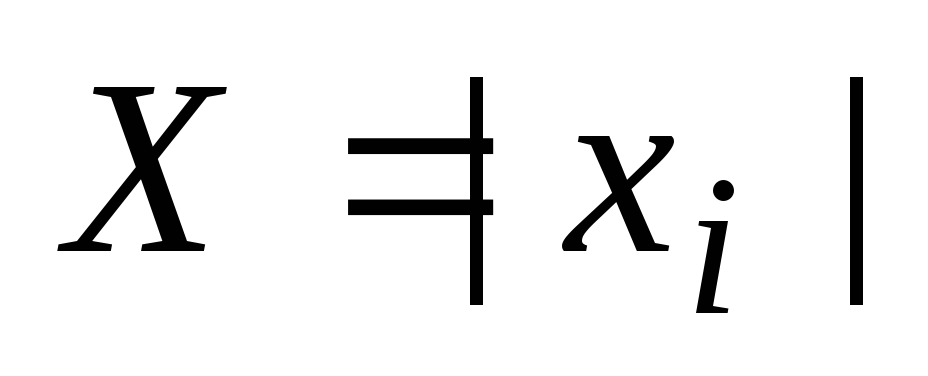
3. Вычислить значения 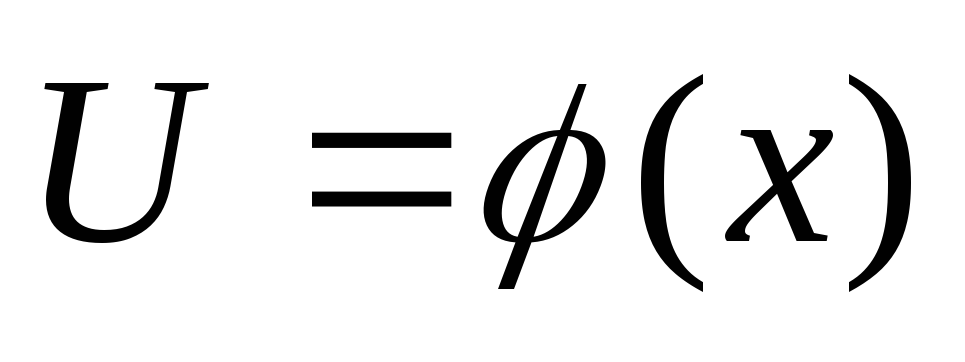, где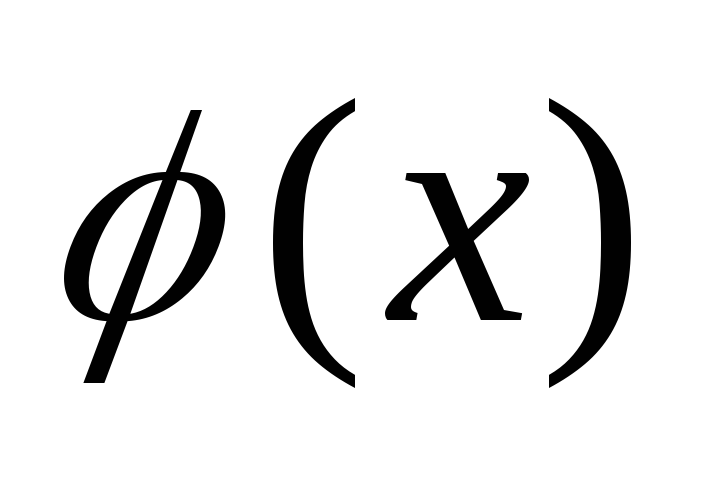- заданная функция.

4. В качестве результата выдать на печать элементы матрицы А, вектораХи значениеU.

Правила получения вектора Хпо матрицеА:

1. i-ый элемент вектораХ– скалярное произведениеi-ой строки матрицыАнаi-ый столбец.

2. i-ый элемент вектораХ– скалярное произведениеi-ой строки матрицыАна первый столбец.

3. Вектор Х– главная диагональ матрицы, преобразованной следующим образом: в начале каждой строки собраны все ее положительные и нулевые элементы, а в конце – все отрицательные при сохранении порядка их следования.

4. Вектор Х– главная диагональ матрицы, преобразованной следующим образом: элементы каждой строки отсортированы по возрастанию.

5. Вектор Х– упорядоченные по убыванию средние арифметические значения элементов строк матрицыА.

6. Строки матрицы Аупорядочить по возрастанию значений элементов ее первого столбца и в качестве вектораХпринять главную диагональ преобразованной матрицы.

7. В качестве элементов вектора Хпринять разность между максимальным и минимальным элементами соответствующей строки матрицыА.

№	Функция формирования матрицы А
1.
2.
3.
4.
5.
6.
7.
8.

Лабораторная работа № 3.

Тема. Программирование итерационных циклов.

Цель работы: Освоить методы программирования, использующие итерационные алгоритмы последовательных приближений получение навыков при использовании рекуррентных выражений.

Задача.

Согласно варианта из приведенного ниже задания вычислить значение некоторой функции в заданном диапазоне изменения аргумента х с заданной точностью. Результаты вычислений оформить в виде таблицы:

Аргумент Х

Значение функции

Сумма (произведение)

Кол-во итераций

№	Вычислительная формула	Диапазон изменения аргумента	Шаг	Точ-ность	Функция
1.
2.
3.		[0.1;0.5]	0.05
4.
5.
6.
7.
8.
9.
10.
11.		[1;1.5]	0.025
12.		[0;1]	0.1
13.		[1;2]	0.1
14.		[0.1;1]	0.1
15.		[0;2]	0.1
16.		[0;1]	0.1
17.		[0;0.8]	0.04
18.
19.
20.		[-0.6;0.6]	0.1
21.		[0.1;1]	0.1
22.		[0;2]	0.1
23.
24.
25.		[0.1;0.5]	0.05