8.2. Лежат ли прямые ab и cd в одной плоскости? Если да, то найдите угол между ними. Если нет, то определите кратчайшее расстояние между ними.

Если прямые AB и CD лежат в одной плоскости, то и эти четыре точки лежать в одной плоскости, следовательно, любые три вектора образованные этими точками тоже лежат в одной плоскости.

Проверим, лежат ли вектора в одной плоскости.

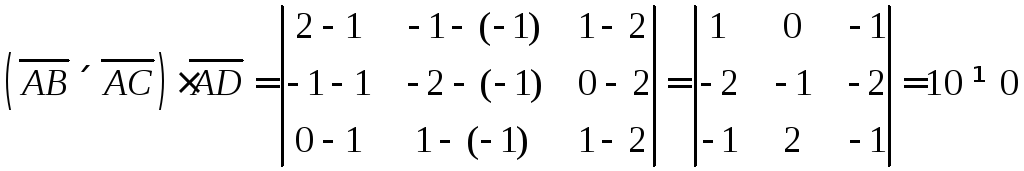
Следовательно, прямые не лежат в одной плоскости

Найдём расстояние между ними, иллюстрация ниже поможет понять ход решение.

Составим уравнение плоскости P, параллельной двум прямым и которая проходит через одну из них, например через АВ. Тогда расстояние от любой точки прямой CD до плоскости P и будет искомым расстоянием между прямыми.

Составим уравнение плоскости, проходящей через точку A и параллельной векторам и.

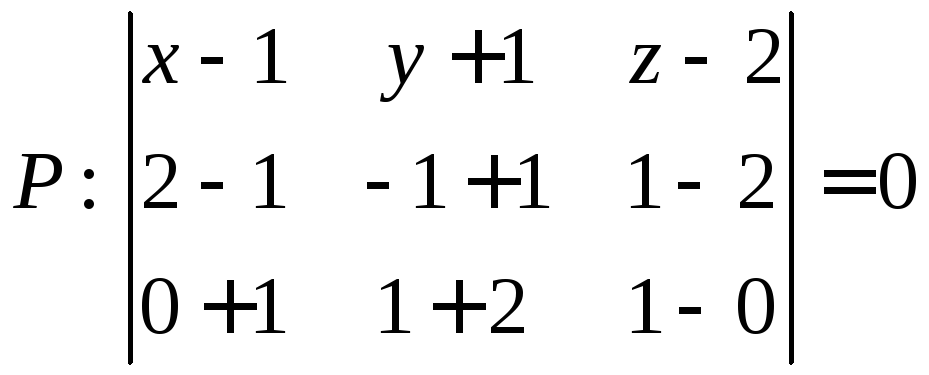
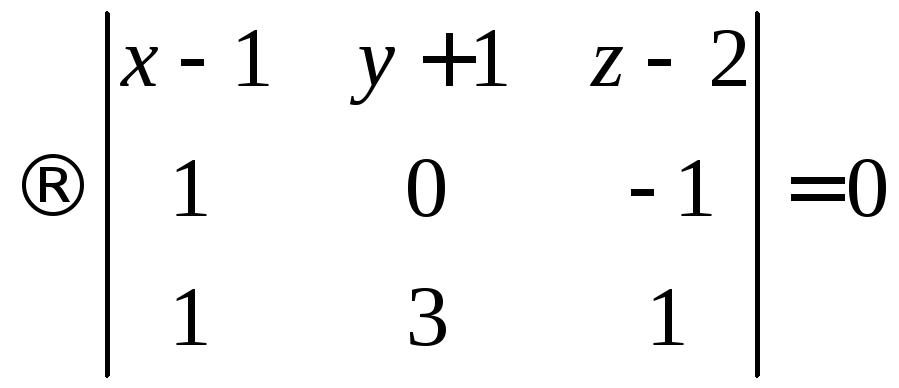
Найдём расстояние от плоскости до точки, принадлежащей прямой ВС, например С.

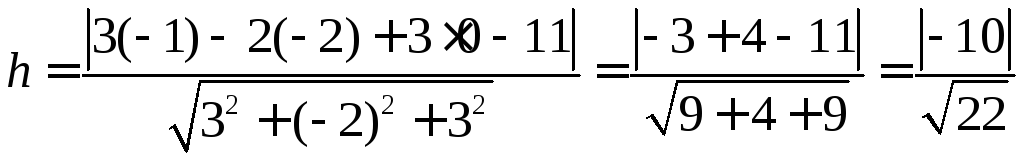
Ответ: .

8.3. Найти точку d1, симметричную точек d относительно прямой, проходящей через точки a и b. Чему равно расстояние от точки d до указанной прямой.

1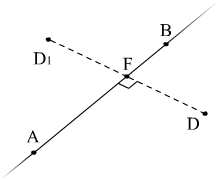) Составим параметрические уравнения прямой АВ.

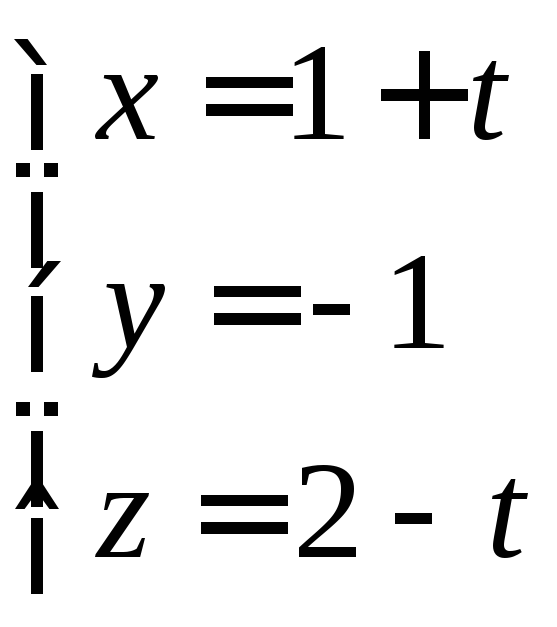
Точка F лежит на прямой АВ, это значит, что при определённом параметре t мы получим координаты этой точки.

2) Так как то их скалярное произведение равно нулю.

Решив это уравнение получим , тогда

Если бы нам было известно две крайние точки, то среднюю мы бы находили как среднее арифметическое. У нас же задача обратная: есть крайняя и средняя точки, нужно найти вторую крайнюю.

Применим формулу.

И найдём расстояние от D до прямой АВ, как длину вектора

Ответ: ,.

8.4. Найти точку пересечения двух прямых и прямой l1 с плоскостью p.

, ,

A = (5, -1, 0), B = (-2, 7, 1), C = (1, 1, -2), D = (12, -15, -7)

AB = (-7 8 1)

СD = (11 -16 -5)

Составим параметрические уравнения прямых:

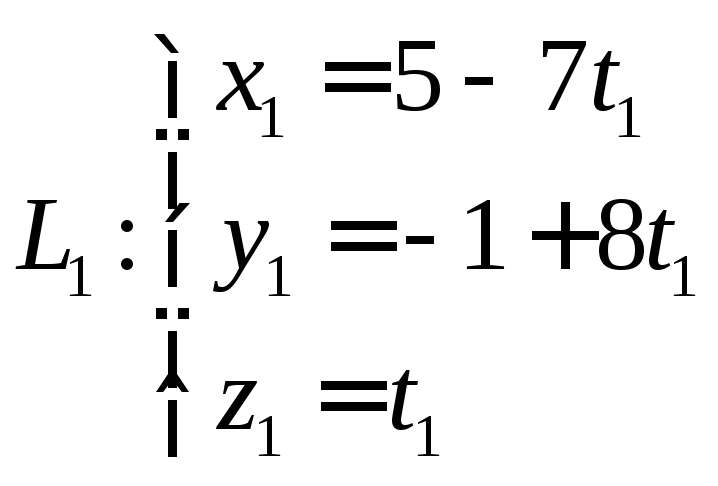
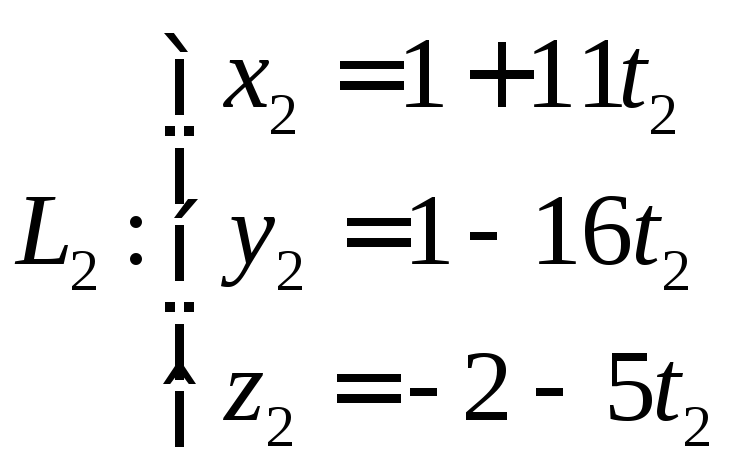
В точке пересечения прямых, координаты точек равны.

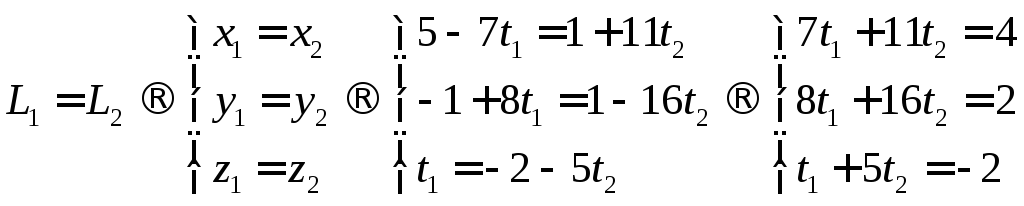
Мы получили систему с двумя неизвестными и тремя уравнениями. Решив её, получим:

Подставляя значения t₁ и t₂ в канонические уравнения прямых, соответственно мы получим координаты точки пересечения.

Найдём пересечение прямой и плоскости. Воспользуемся параметрическими уравнениями прямой и подставим правые части в уравнение плоскости.

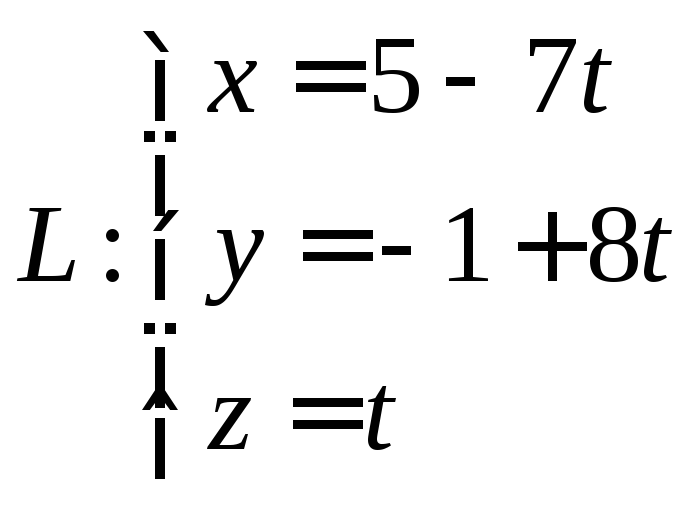
Решим данное уравнение

Подставим полученное число в систему параметрических уравнений.

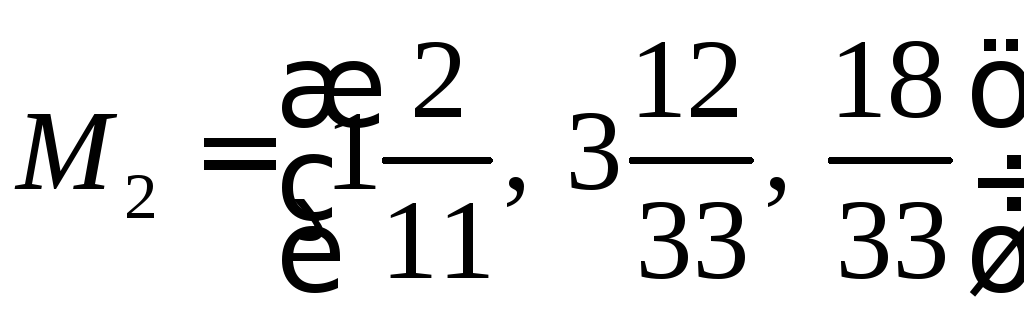
Ответ: , .

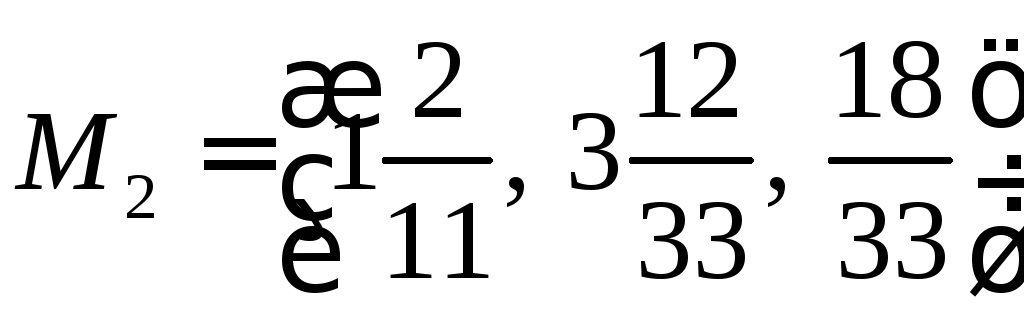9. Прямая на плоскости

Немного теории

Каноническое уравнение прямой

–точка прямой

–направляющий вектор

Параметрические уравнения прямой

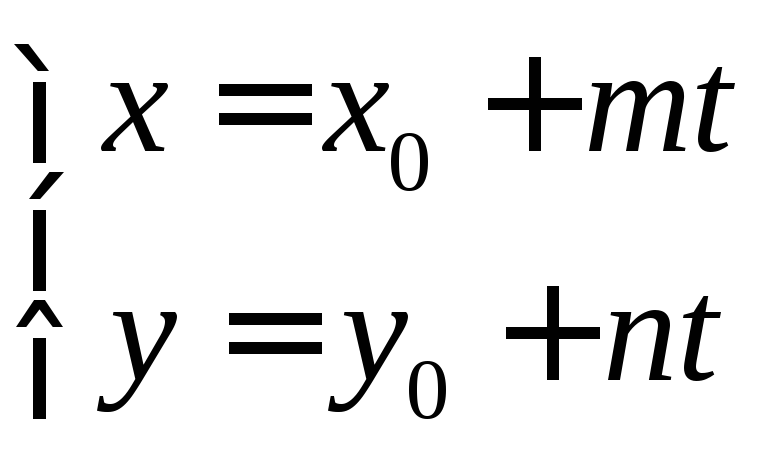
Общее уравнение прямой

–вектор - нормаль

Уравнение прямой с угловым коэффициентом

k – тангенс угла к оси OX

y – смещение вверх по оси OY

Основные зависимости

, ,,,

Примеры

Даны вершины некоторого треугольника A, B, C. Требуется найти:

A(1; 1), B(-1; 3), C(3, -3)

9.1 периметр треугольника.

Периметр треугольника – это сумма всех сторон, - это сумма модулей векторов. Модуль векторов на плоскости находится аналогично, как и в пространстве.

, ,.

, , .

Ответ:

9.2 уравнение и длину высоты, проведённой через вершину С.

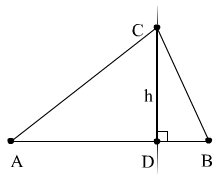
Составим уравнение прямой AC.

,

Составим уравнение прямой CD: через точку C и нормалью AB.

Найдём точку D, как пересечение прямых AC и BD.

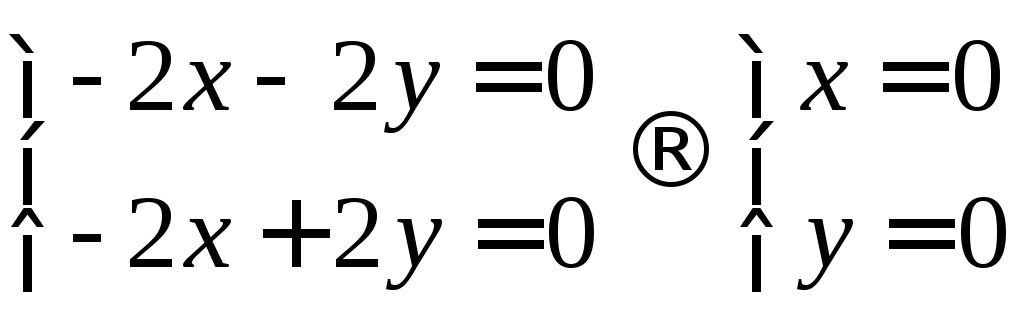
Найдём координаты вектора BD и его длину.

,

Ответ: , .

9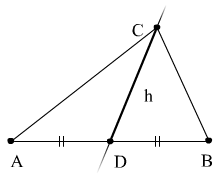.3 уравнение медианы, проведённой из вершины В.

Медиана CD, проходит через среднюю точку отрезка АВ.

Составим уравнение прямой по точкам CD.

Ответ:

9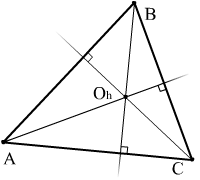.4 точку пересечения высот треугольника

Высоты треугольника пересекаются в одной точке. Значит достаточно найти вторую высоту, например из точки А, и найти точку пересечения, с уже полученной высотой.

A(1; 1), B(-1; 3), C(3, -3)

Составим уравнение прямой, проходящей через точку А и перпендикулярной прямой ВС.

Высоту, проведённую из вершины С, мы ранее получили.

Найдём точку пересечения высот

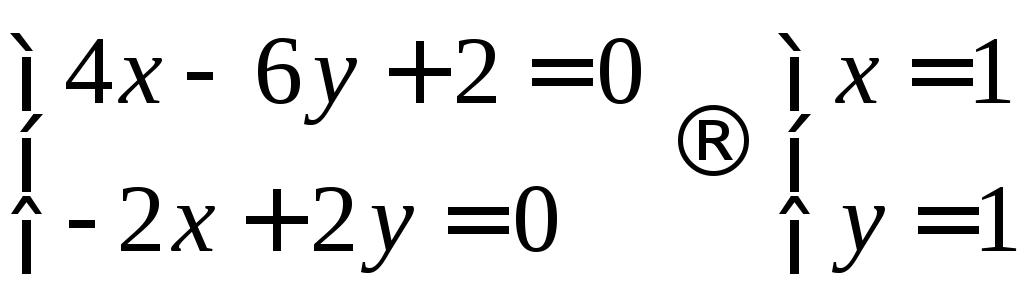
Ответ: O_h(1, 1).

9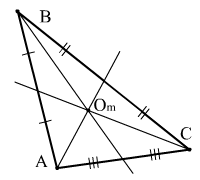.5 точку пересечения медиан треугольника

Медианы также как и высоты треугольника пересекаются в одной точке.

Найдем медиану, проходящую через вершину А.

Медиана, проведённая из вершины С, нам уже известна.

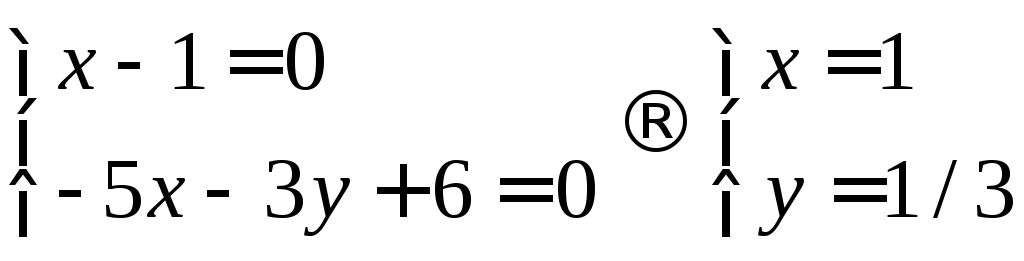
Ответ: O_m(1, 1/3).

9.6 внутренний угол в радианах

A(1; 1), B(-1; 3), C(3, -3)

Углы между векторами на плоскости находятся также как и в пространстве.

Найдем углы между векторами.

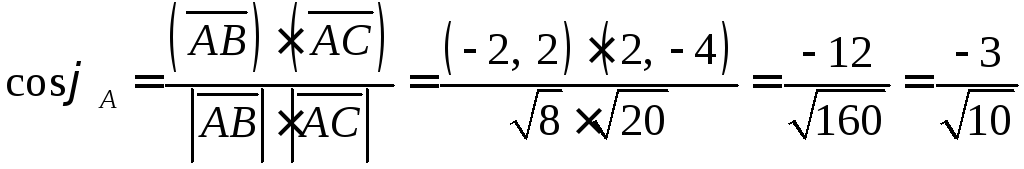
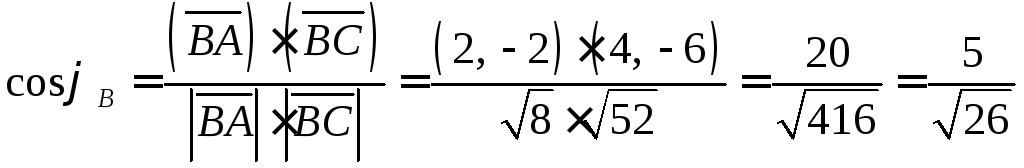
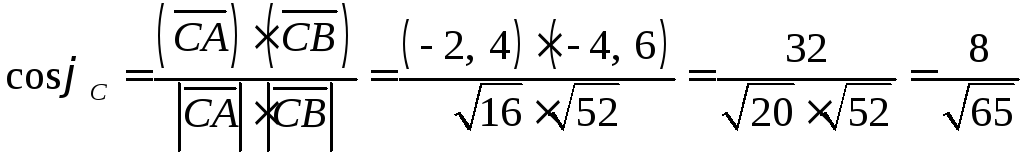
Ответ: ,,

Примечание. Можно проверить правильность решения, сложив все углы. Если получится , значит, решение верно.

9.7 уравнение прямой, проходящей через вершину В под углом к стороне ВС

Угол между прямыми можно измерять по угловым коэффициентам этих прямых.

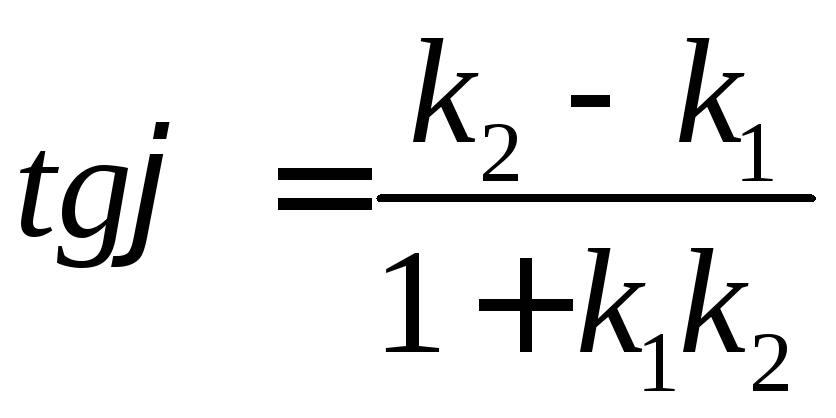
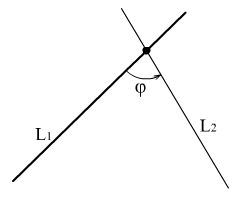
Угол в данной формуле находится в сторону, против часовой стрелки, от прямой с коэффициентом k₁ к прямой с коэффициентом k₂. Заданный угол имеет положительное направление, поэтому искомый коэффициент k₂.

Найдём угловой коэффициент прямой BC.

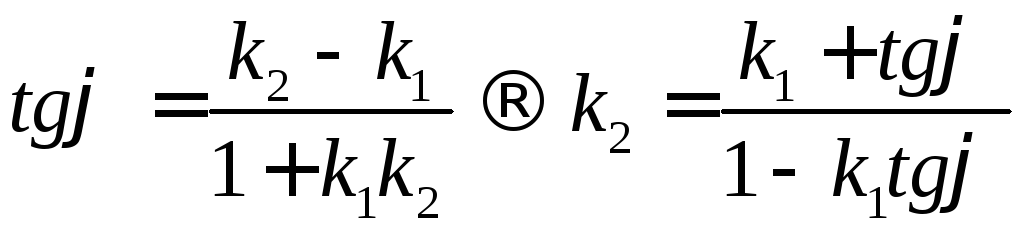
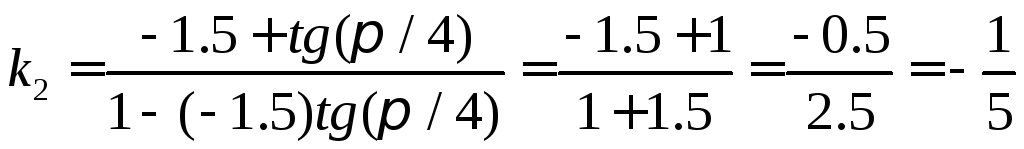
По коэффициенту числителя составим сонаправленный вектор

Составим уравнение требуемой прямой, проходящей через точку В.

Ответ:

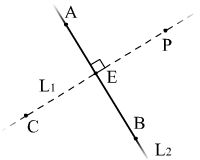
9.8 точку P, симметричную точке С относительно прямой АВ.

Составим уравнение прямой L₁ проходящей через точку C и перпендикулярной

Составим уравнение прямой АВ.

Найдём точку пересечения этих прямых

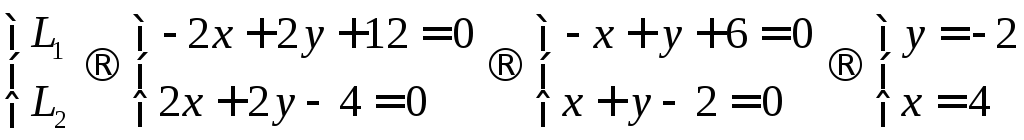
Точка Е является средней на отрезке СР, найдем Р по Е и С.

Ответ:

9.9 площадь треугольника, образованного осями координат и прямой АС.

Составим уравнение прямой АС

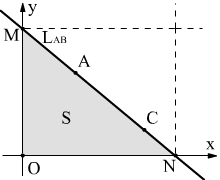
Найдем точки пересечения прямой с осями координат

Если перемножить эти координаты, то получим площадь прямоугольника. Площадь же треугольника в два раза меньше.

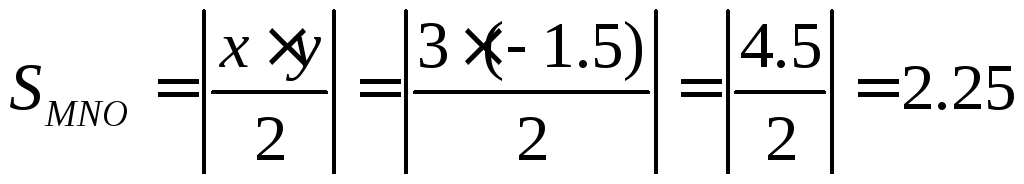
Ответ: S = 2.25

10. Кривые второго порядка

Немного теории

Общий вид кривой второго порядка

Далее, приводится неформальное описание параметров

A – «сплюснутость» по оси OX

B – поворот относительно центра

C – «сплюснутость» по оси OY

D – смещение по оси OX

E – смещение по оси OX

F – общий размер

Примечание. Не стоит буквально понимать описание коэффициентов. Изменение одного из коэффициентов влияет на несколько характеристик. Изменение коэффициентов смещения и вращения влечет к изменению размеров или даже к изменению типа кривой. Однако, если будет В=0, то кривая не будет повёрнута, а если D = 0 и E = 0 то её центр не будет смещен относительно начала координат. Далее, во всех уравнениях. для простоты, коэффициент В принимается равным нулю.

Приведение уравнения кривой к каноническому виду.

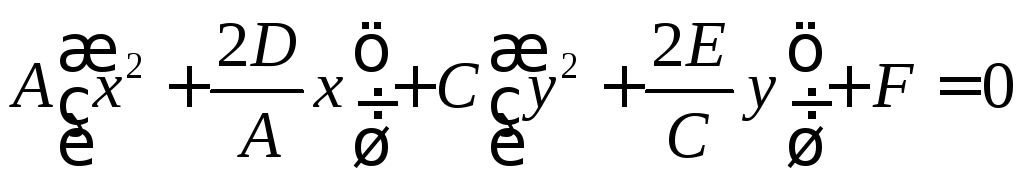
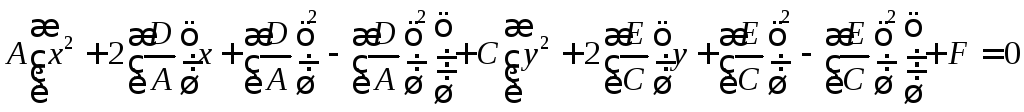
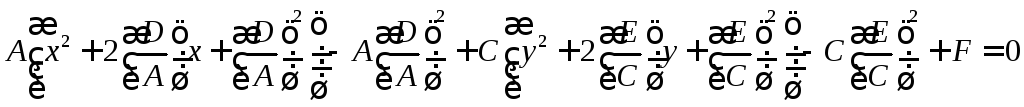
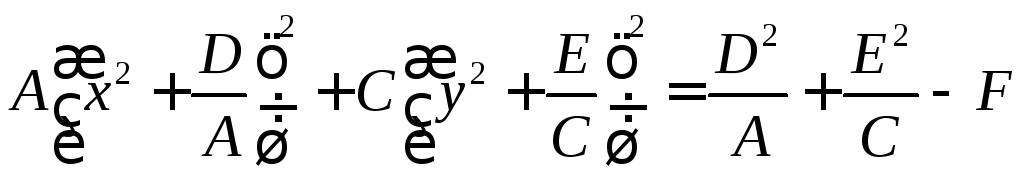
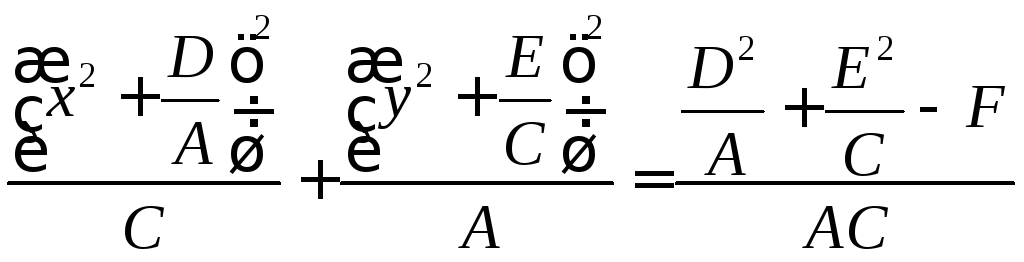
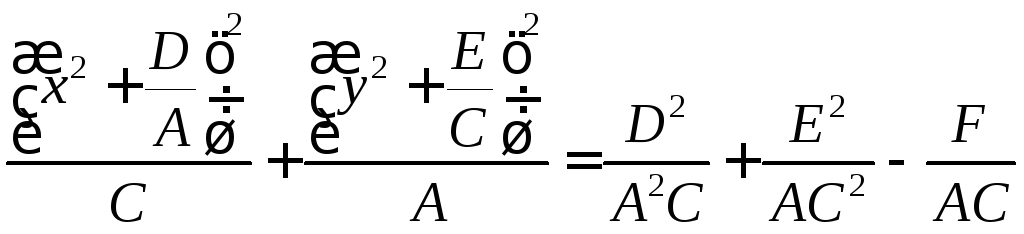, заменим

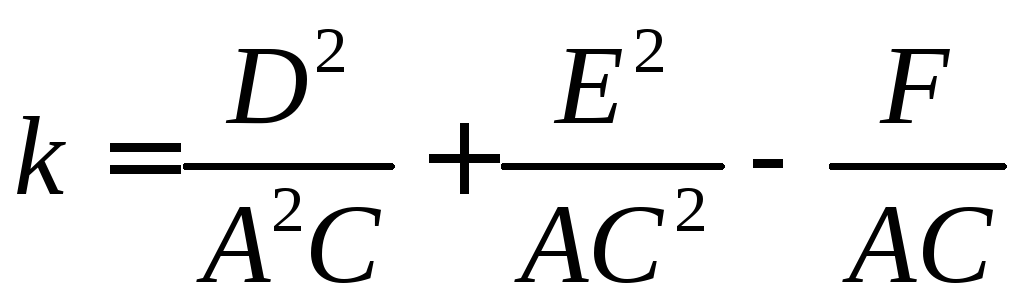
Получим уравнение кривой в каноническом виде

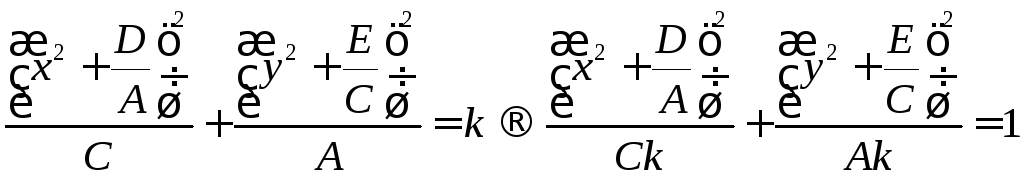
Примеры