2.3. Решить матричное уравнение
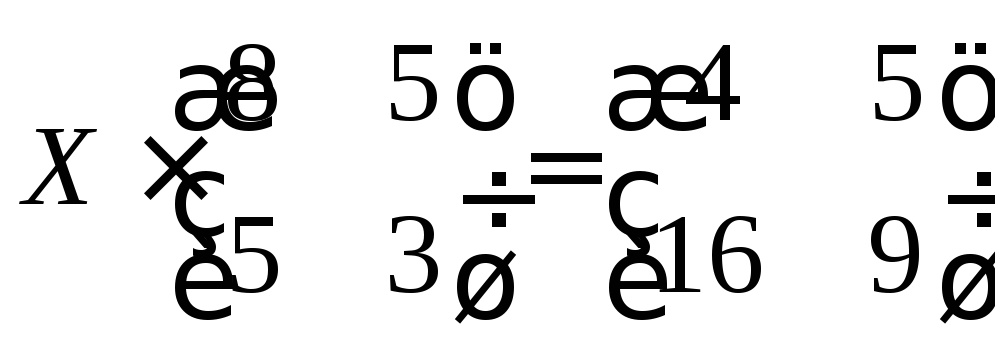
В общем виде уравнение решается
Умножим обе стороны на А-1 справа.
Нам необходимо найти обратную матрицу и выполнить умножение.
,
,
,
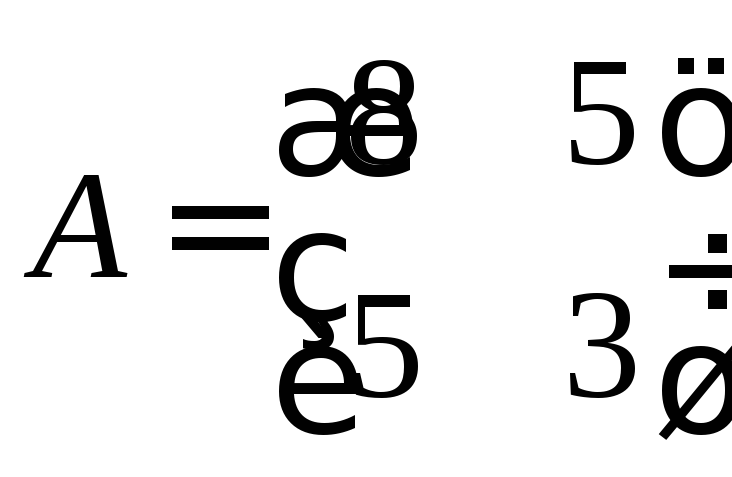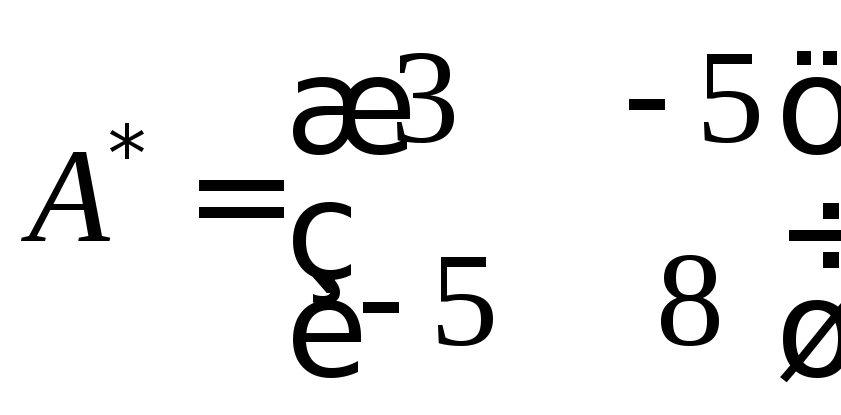
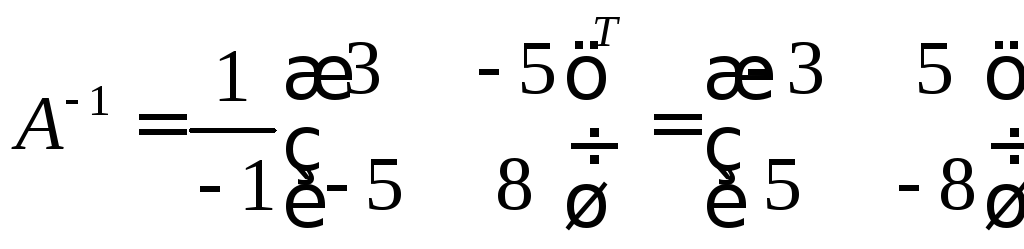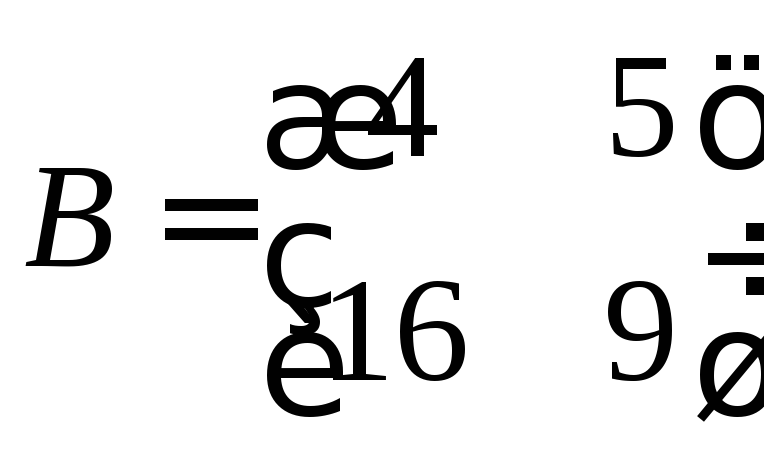
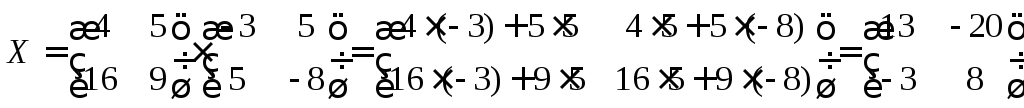
Ответ:
.
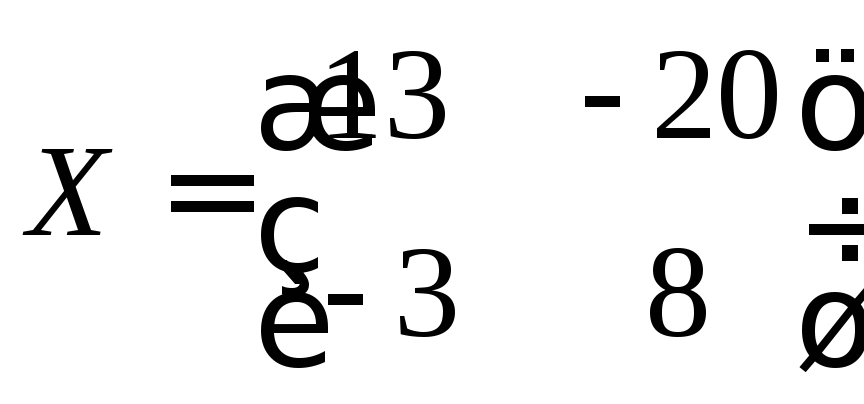Чтоб убедиться в правильности, можно
выполнить проверку.
Примечание. Имеет больше значение то, с какой стороны находится Х.
Решение систем линейных уравнений
Дана система линейных алгебраических уравнений
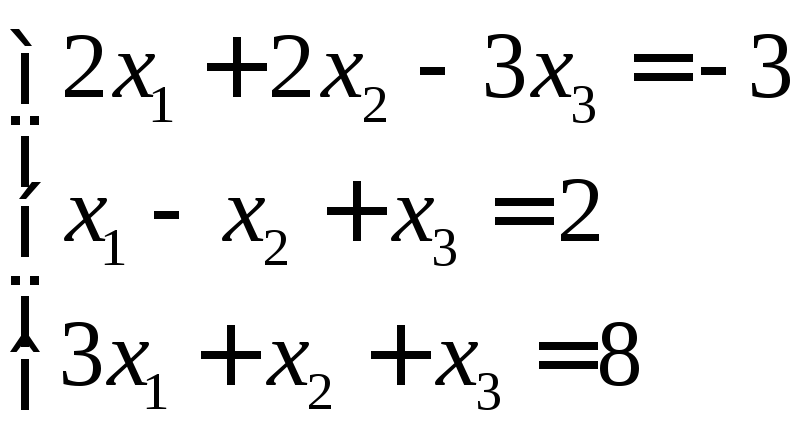
Необходимо решить данную систему. Прежде всего, нужно найти определитель матрицы коэффициентов. Если определитель равен нулю, то система не имеет решения.
Далее показано три метода решения.
3.1. Решить методом Гаусса
Для удобства выпишем матрицу коэффициентов
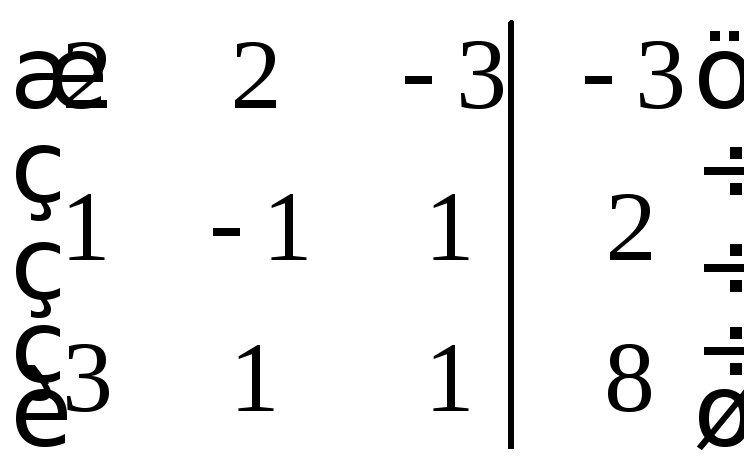
Далее, нам нужно привести матрицу к треугольному виду, т.е. чтоб ниже главной диагонали были нули, а на диагонали – единицы. Для удобства, также поменяем первую и вторую строки местами для того чтоб верхний левый элемент был равен единице (что делать не обязательно).
Ко второй строке прибавим первую, умноженную на (-2), для того, чтоб первый элемент второй строки стал равным нулю. Какими станут значения других элементов этой строки, пока что нас не волнует.
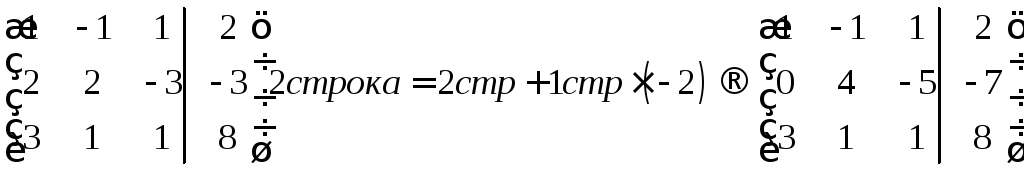
К третьей строке прибавим первую, умноженную на (-3), для того, чтоб первый элемент третьей строки стал равным нулю.
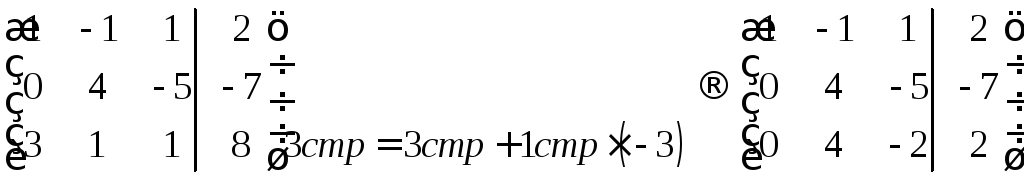
К третьей строке прибавим вторую, умноженную на (-1), для того, чтоб второй элемент третьей строки стал равным нулю.
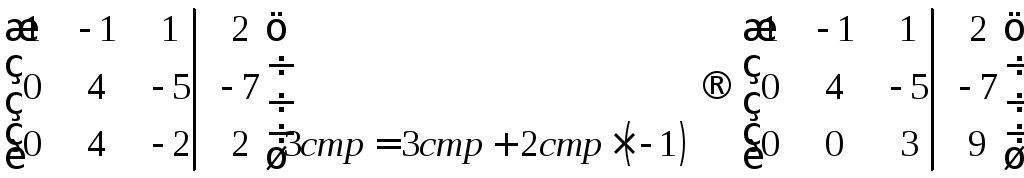
Приведя матрицу к требуемому виду можно находить значения неизвестных:
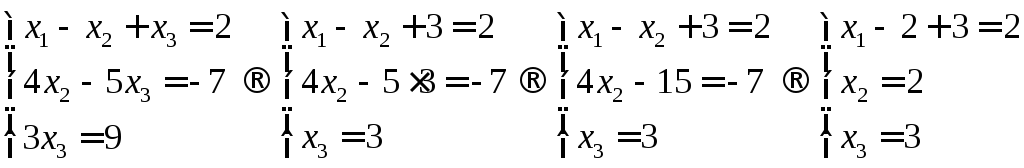
Откуда получим ответ
Ответ:
,
,
.
Ответ можно было также найти при дальнейшем преобразовании матрицы. Для этого нужно привести матрицу коэффициентов при неизвестных к виду единичной матрицы.
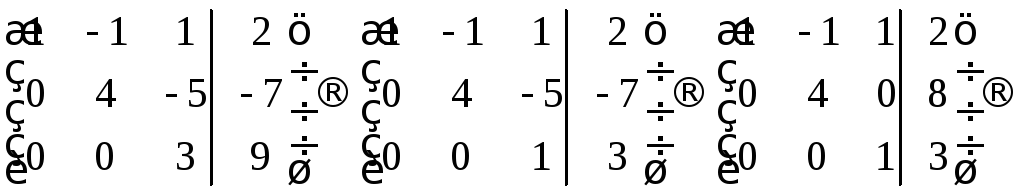
Из последнего, можно увидеть, чему равна каждая неизвестная.
Ответ:
,
,
.
Примечание. Метод Гаусса, на первый взгляд может показаться запутанным, однако, но является наименее трудозатратным и широко применяется.
3.2. Решить по правилу Крамера.
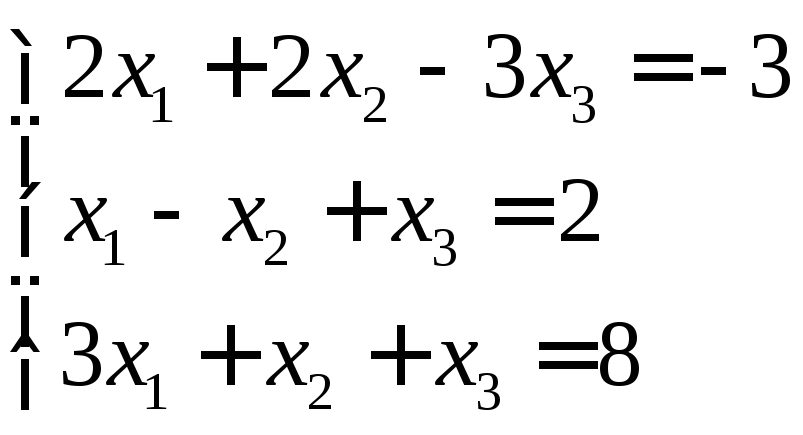
Выпишем матрицу коэффициентов
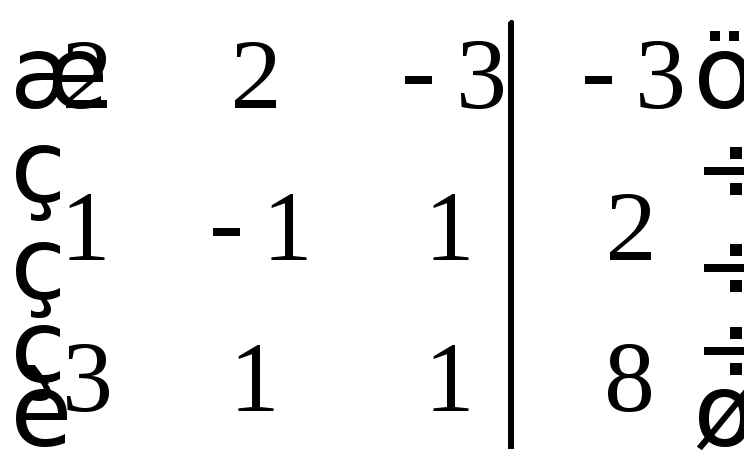
Найдём основной
и дополнительные определители.
Определитель ещё обозначается символом
.
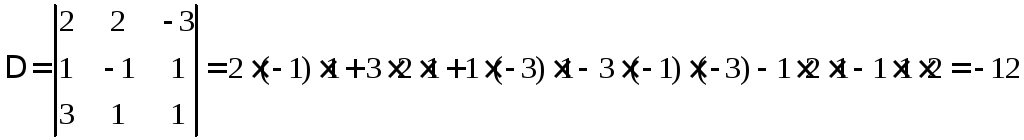
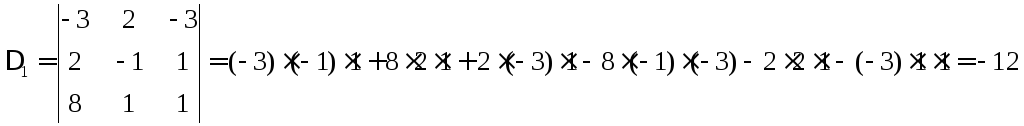
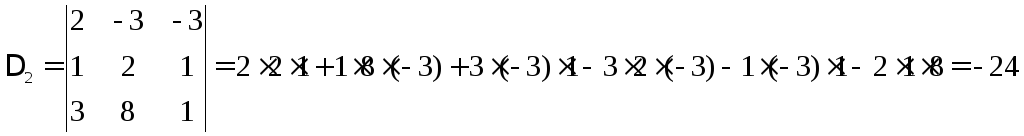
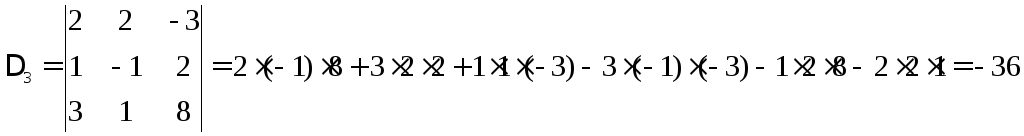
Находим неизвестные
,
,
Ответ:
,
,
.
Данный метод кажется простым, но это только для системы с тремя неизвестными, при увеличении количества уравнений сложность резко возрастает.
3.3. Решить матричным методом.
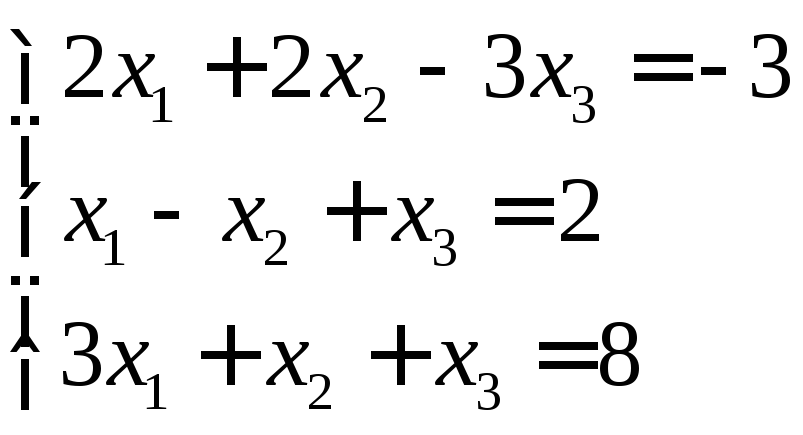
Решение матричного уравнения в общем виде
,
где
,
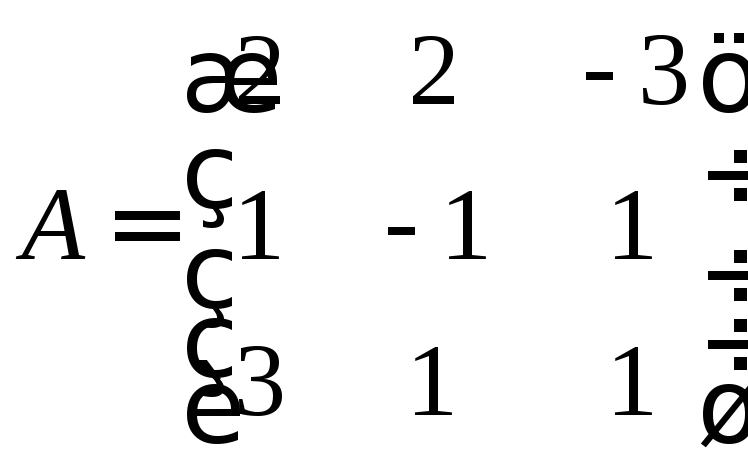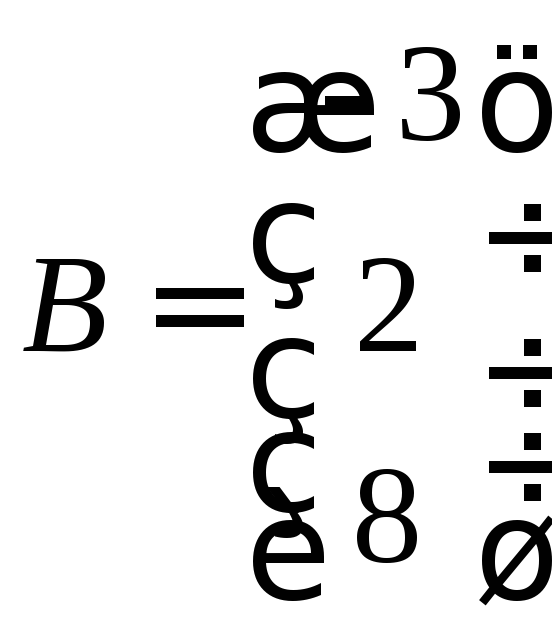
Найдём матрицу, обратную А.
,
,
, 
,
, 
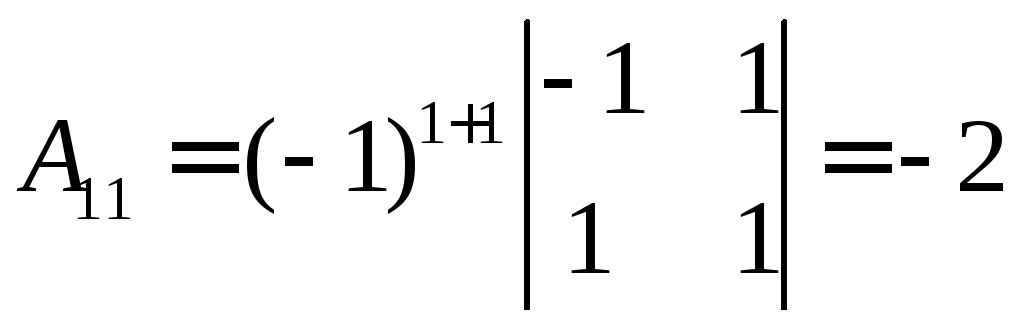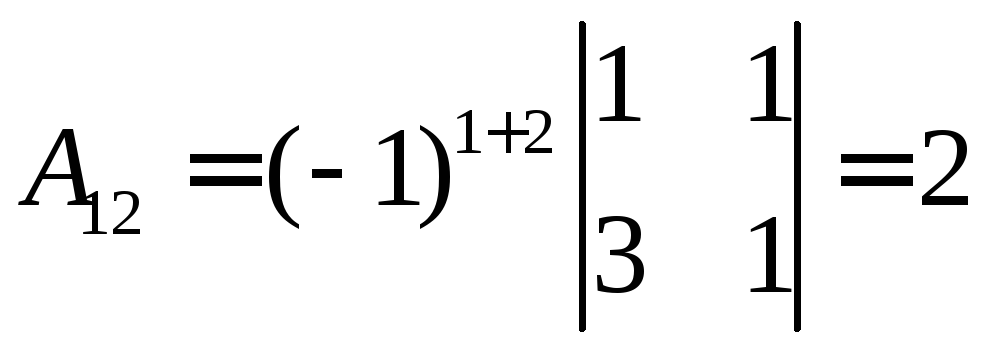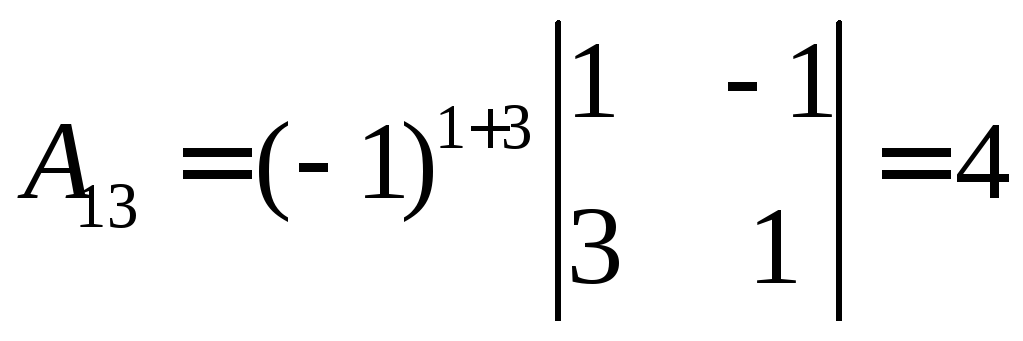
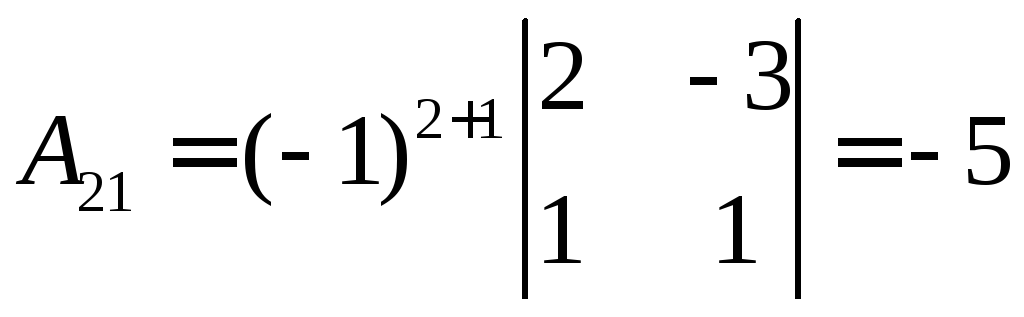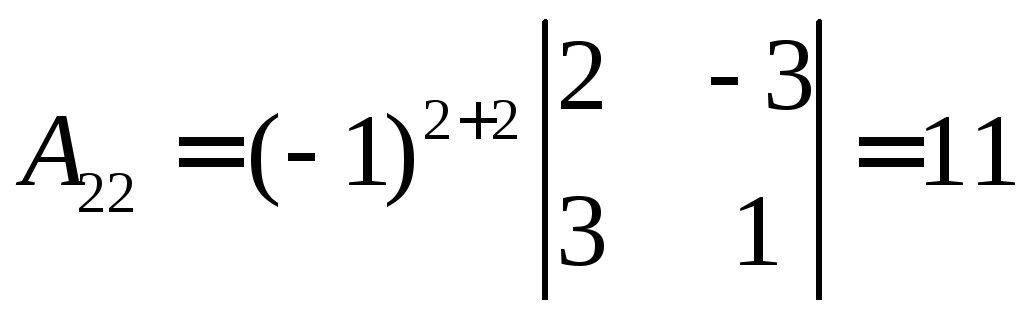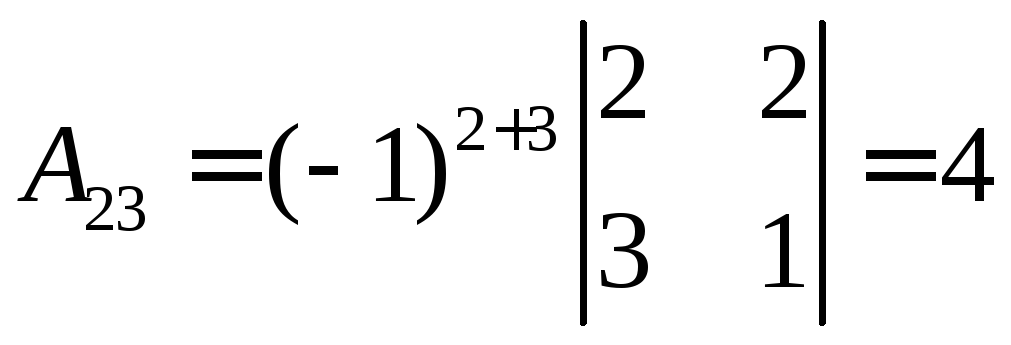
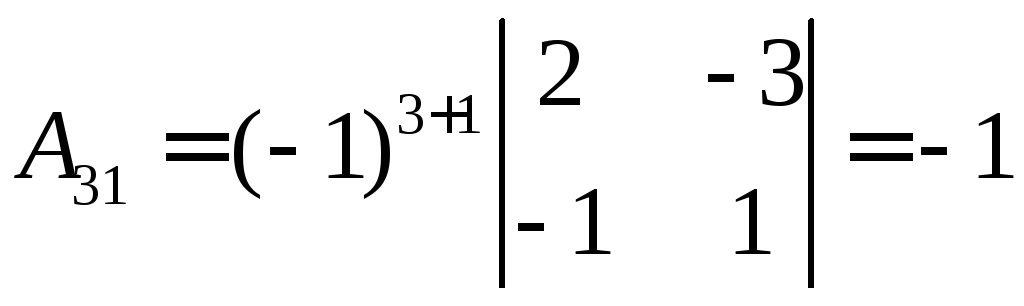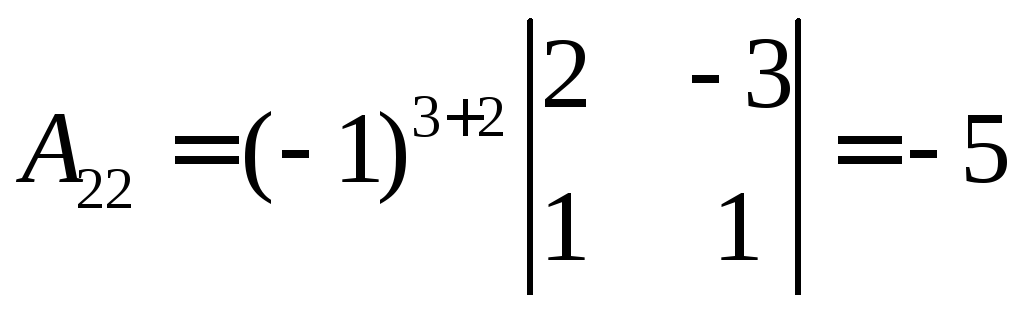
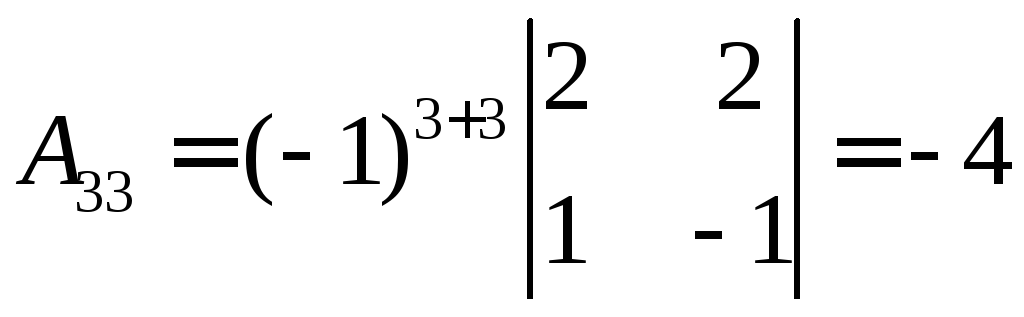
Союзная матрица
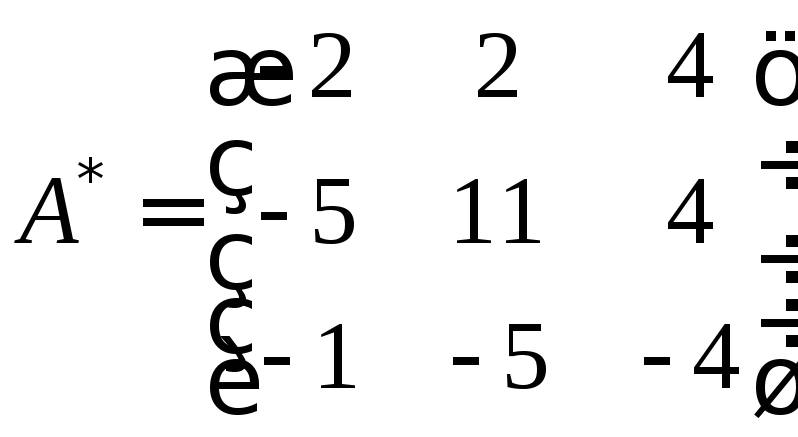
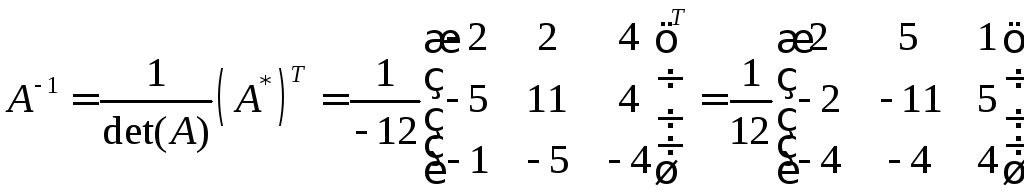
Т.к. элементы матрицы не делятся нацело на 12, оставим делитель за скобками, это не будет ошибкой.
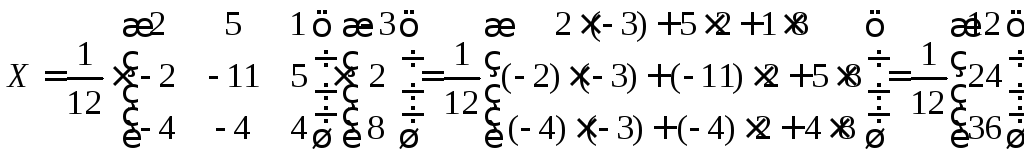
Теперь можем разделить на определитель
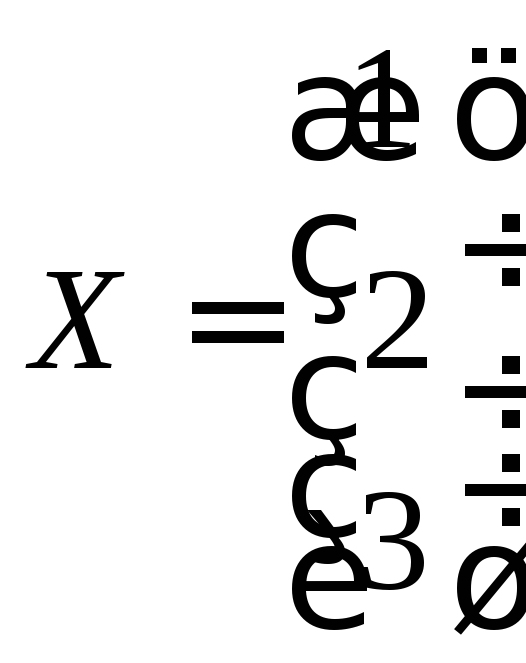
Ответ:
,
,
.
Примечание. При перемножении матриц и скаляра, действует переместительный закон, но только на скалярное число.
Ранг матрицы. Разрешимость систем
4.1. Определить ранг матрицы
а)
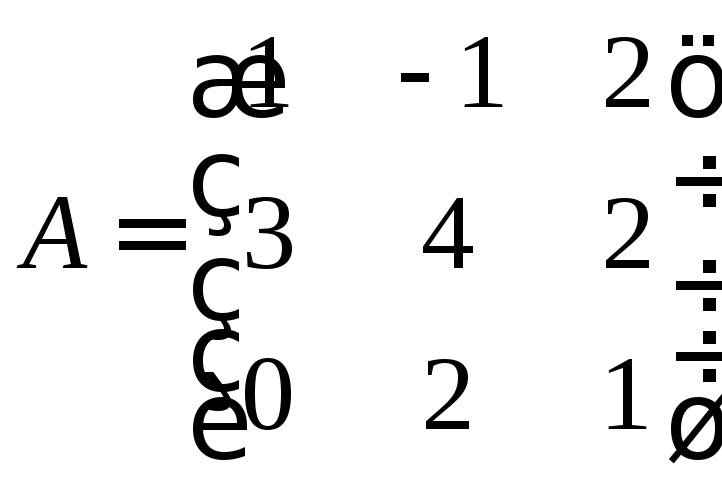
Найдем определитель данной матрицы
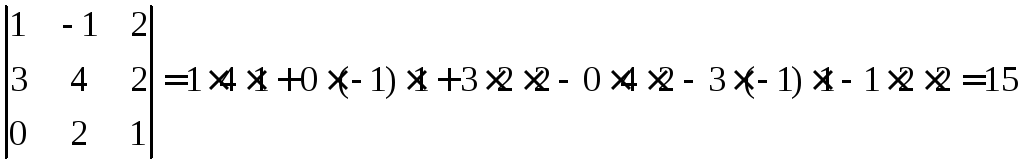
Определитель не равен нулю, значит, ранг матрицы равен ее размерности
Ответ: rank(A) = 3.
б)
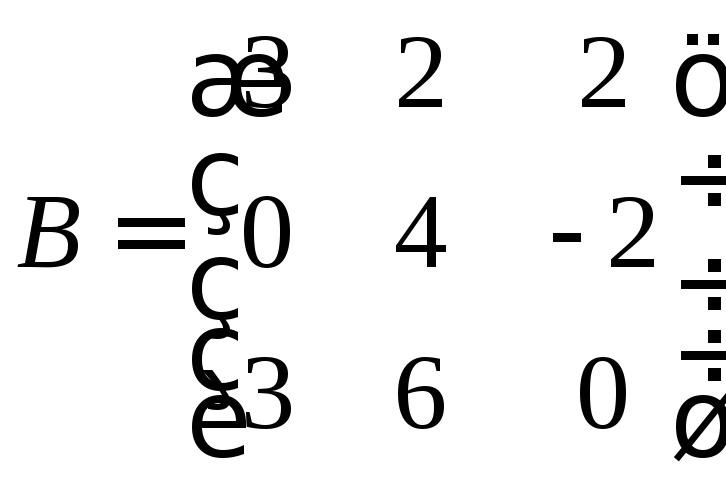
Найдём её определитель
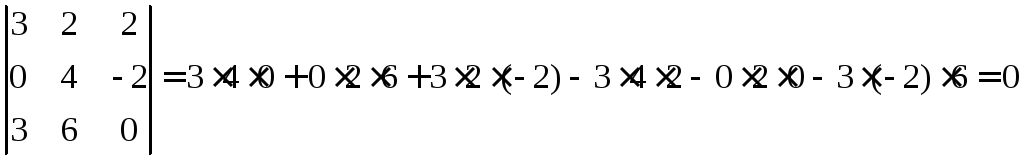
Определитель матрицы равен нулю, значит, ранг матрицы не будет равен её размерности. Из матрицы В составим матрицы меньшей размерности (2х2) путём удаления одной строки и одного столбца. Таких комбинаций будет девять. Если хоть одна такая матрица не даст нулевой определитель, то ранг всей матрицы будет равен двум.
Из матрицы В отбросим первую строку и столбец и найдём определитель получившейся матрицы.
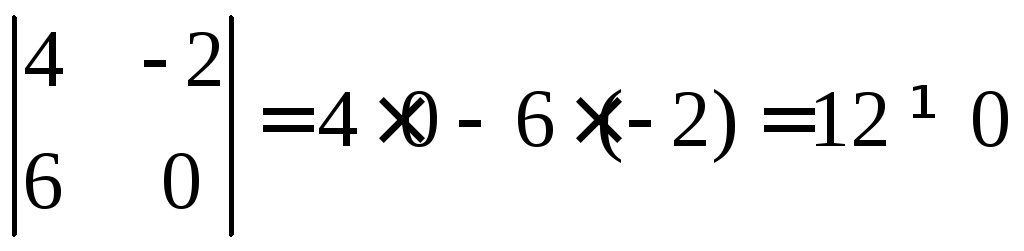
Значит ранг матрицы В равен размерности последней матрицы
Ответ: rank(В) = 2.
в)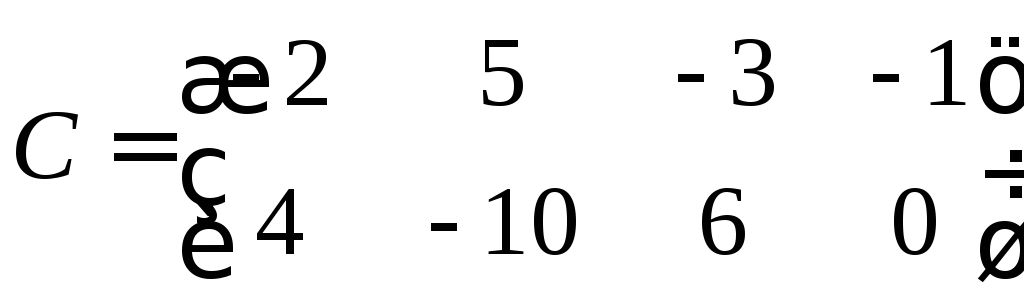
Данная матрица прямоугольная, а определитель можно найти только квадратной. Значит будем составлять квадратные матрицы путём отбрасывания лишних столбцов.
1) Возьмём два первых столбца.
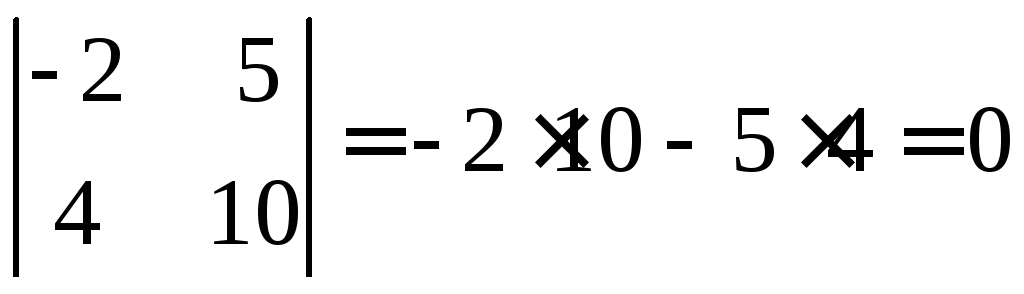
2) Возьмём первый и третий столбцы.
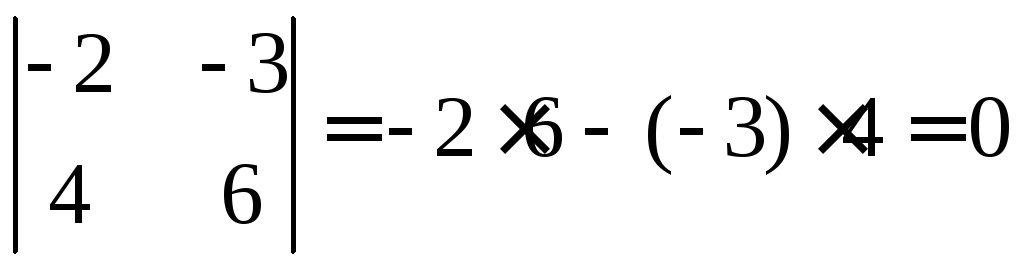
3) Возьмём первый и четвёртый столбцы.
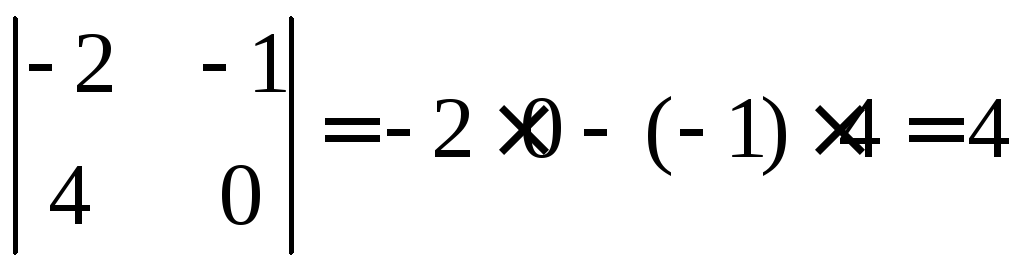
Ранг матрицы C равен размерности данной матрицы, несмотря на то, что два первых определителя равны нулю.
Ответ: rank(С) = 2.
Примечание. Данный метод нахождения ранга матрицы становится затруднительным при повышении размерности матрицы. Далее будет показано применение метода Гаусса для нахождения ранга матрицы.