4.2. Определение ранга матрицы методом Гаусса.

Приведём матрицу к виду трапеции.

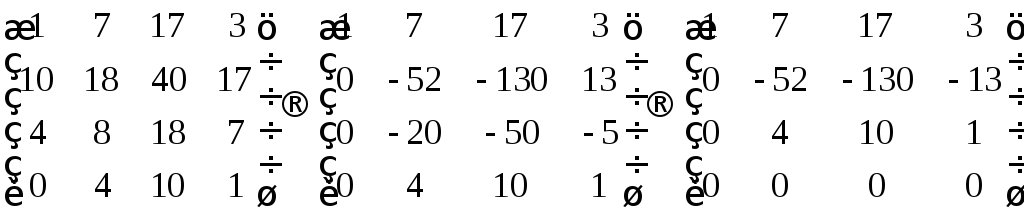
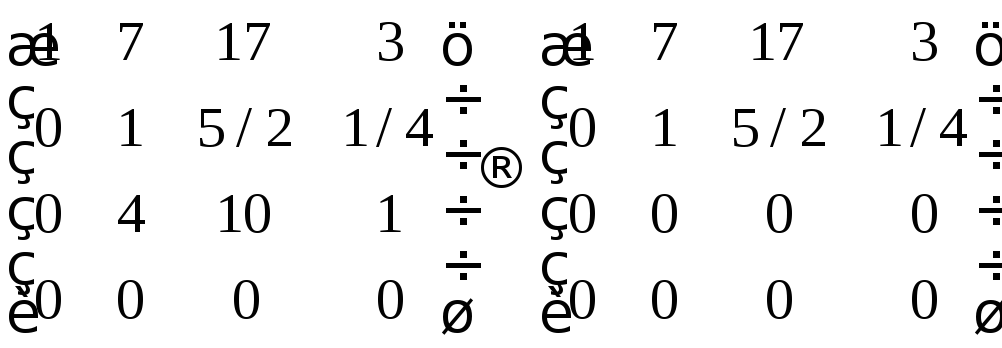
Как видим, получили матрицу, в которой два ряда сократились, а остальные два ряда не сокращаются. Рангом матрицы является количество несокращаемых рядов в матрице.

Ответ: ранг матрицы равен 2.

4.3. Дана система, где a и b некоторые константы.

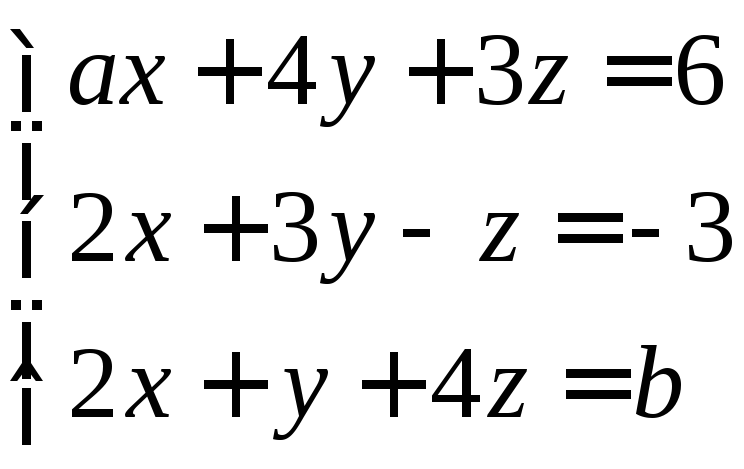
а) При каких a и b система имеет единственное решение.

Система имеет единственное решение, если определитель матрицы коэффициентов не равен нулю.

,

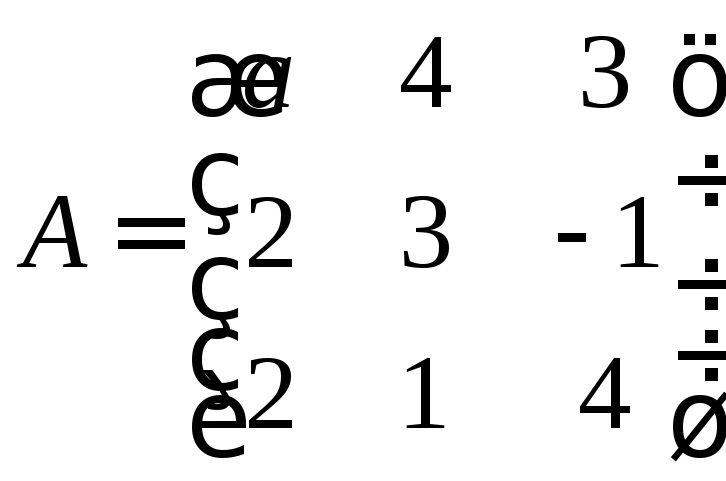
Определим, при каком значении а, определитель матрицы А не будет равным нулю.

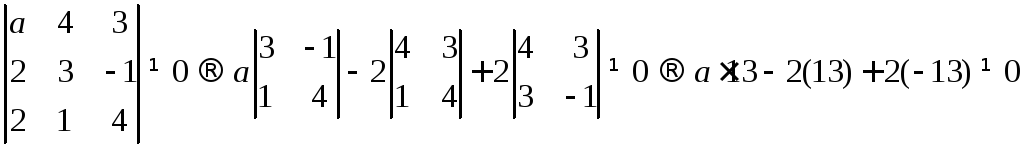
Ответ: система имеет решение при ,.

Обратите внимание, что определитель был раскрыт по первому столбцу. Если бы мы применяли метод треугольника, то пришлось бы собирать подобные при неизвестной а. Также стоит обратить внимание на то, что на решаемость системы не влияет столбец ответов B.

б) При каких значениях a и b система не имеет решения.

Если определитель системы равен нулю, система не имеет единственного решения, в таком случае система, либо не имеет решения вовсе, либо имеет бесконечное множество решений.

Система не имеет решения если:

rank(A') > rank(A), где А' – расширенная матрица

В основную матрицу подставим, а = 4.

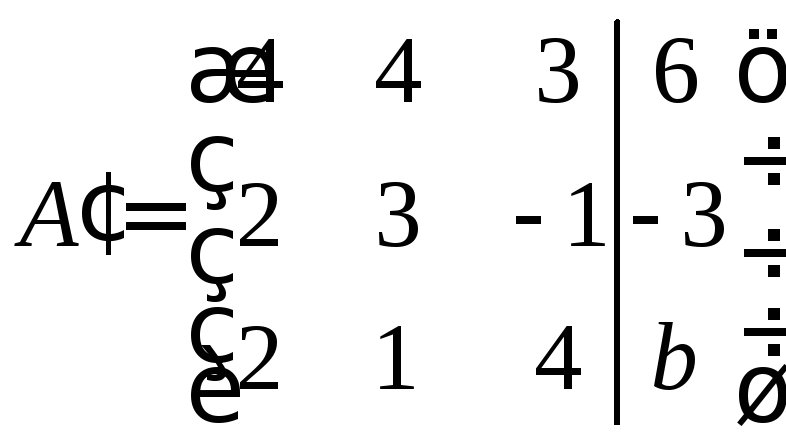
Для начала найдём ранг матрицы А:

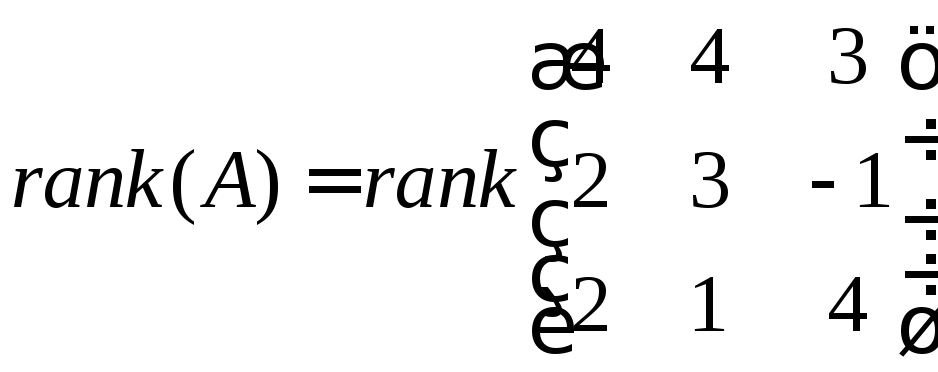
Определитель данной матрицы равен нулю, т.к. мы подставили искомую а = 4. Следовательно, ранг матрицы ниже 3-х.

Составим из матрицы А матрицу меньшего размера и найдём её определитель. Возьмём матрицу 2х2 построенную из левых верхних элементов матрицы А.

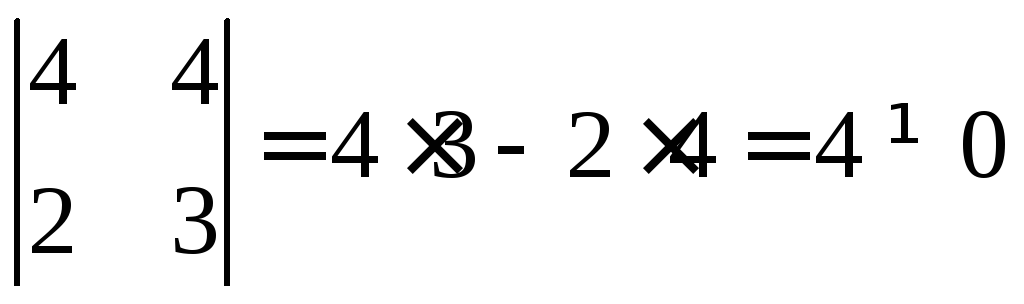
Определитель не равен нулю, значит ранг матрицы А = 2.

Чтоб система не имела решений ранг матрицы A' должен быть больше 2-х.

Определим, при каком значении b ранг матрицы А' не будет равен нулю.

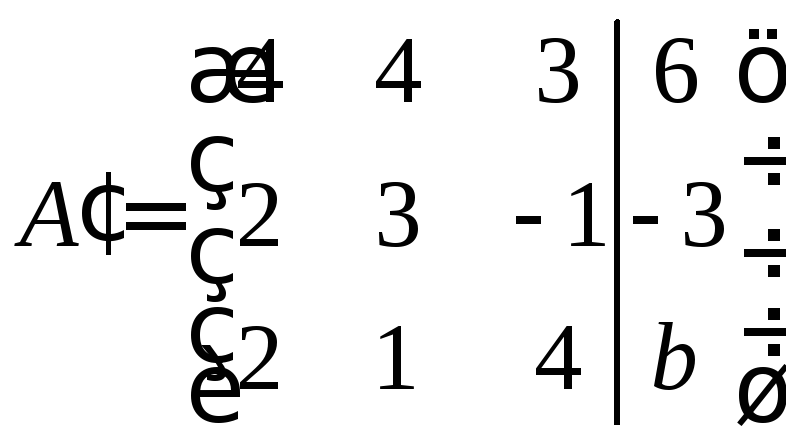
Найдём определитель подматрицы А'.

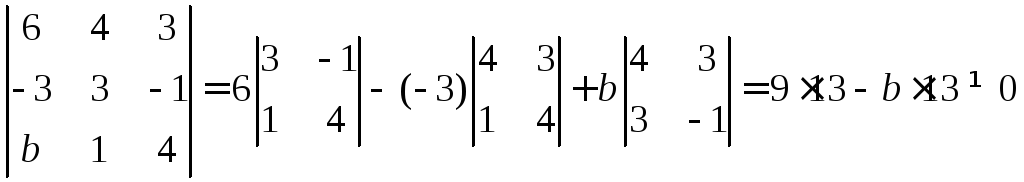
Получаем .

Проверим для двух других случаев

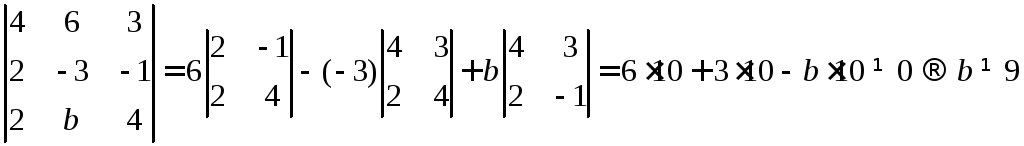
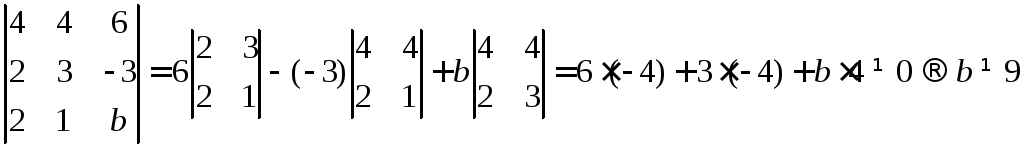
Как видим, для всех комбинаций расширенной матрицы .

Ответ: система не имеет решение при ,.

в) При каких a и b система имеет бесчисленное множество решений.

Если rank(A') <= rank(A), а это будет в случае если b = 9.

Ответ: система имеет бесконечное количество решений при ,.

4.4. Имеет ли система однородных уравнений нетривиальное решение. Если имеет, найти его.

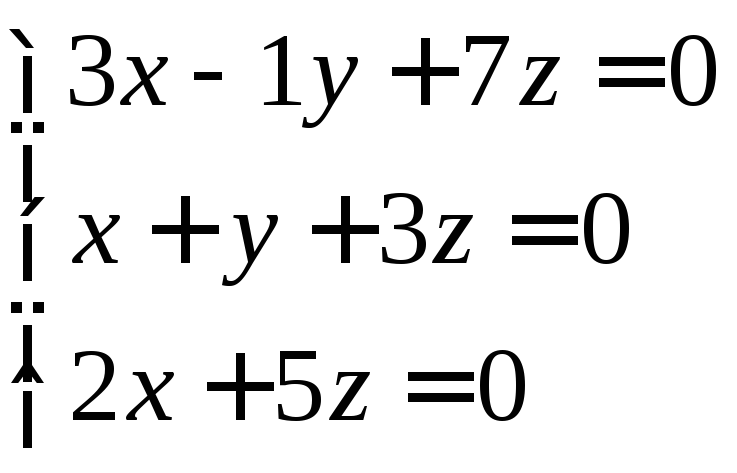
Однородное уравнение всегда имеет нулевое решение, но это решение называется тривиальным. Чтоб система однородных уравнений имела нетривиальное решение, её определитель должен быть равен нулю. Если система однородных уравнений имеет нетривиальное решение, то это бесконечное множество решений.

Найдём определитель

,

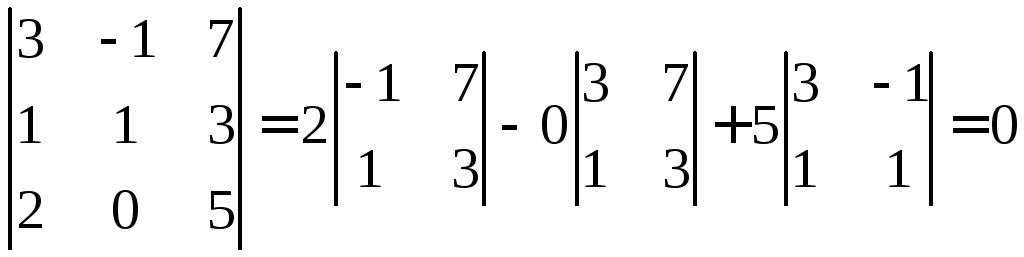Следовательно, система имеет нетривиальные решения.

Приведём матрицу коэффициентов к виду трапеции.

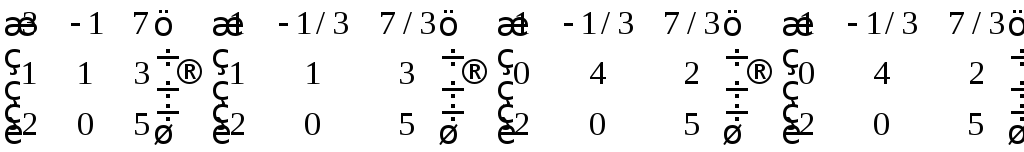
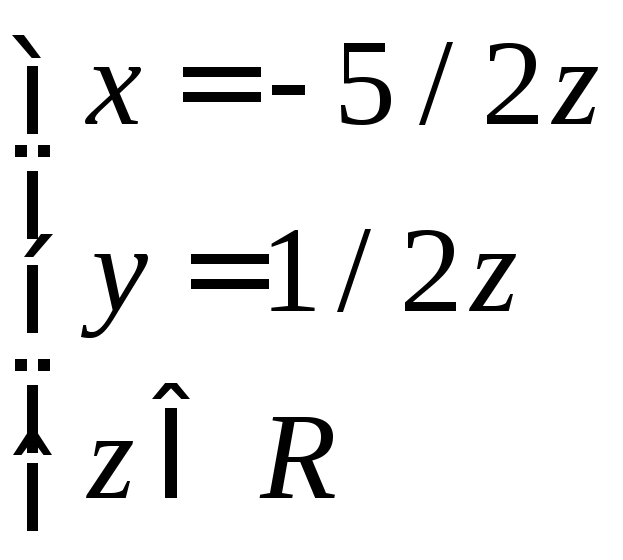
Ответ: система имеет решение .

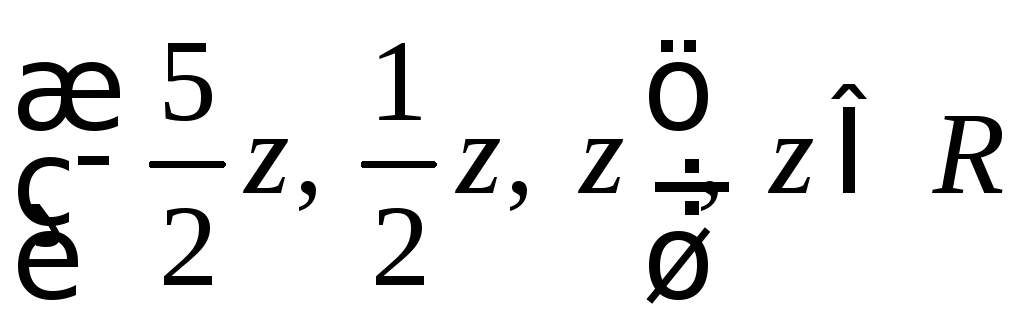Примечание. То, что в ответе присутствуют свободные элементы, это нормально. Выражение полностью исчерпывает ответ. Для любого z ответ будет верным, т.е. ответов бесконечное множество.

5. Линейное пространство

5.1. Образует ли линейное пространство, заданное множество, в котором определены сумма любых двух элементов a и b и произведение любого элемента a на любое число .

Немного теории

Линейное (векторное) пространство над числовым полем K называется множество объектов L любой математической природы, для которых определены операции сложения и умножения.

L – элементы математической природы

K – числовое поле

–операция сложения:

–операция умножения

,

Линейное пространство должно удовлетворять следующим свойствам

1. ,- замкнутость операций

2. - коммутативность сложения

3. - ассоциативность

4. - существование «нулевого» элемента

5. - существование «отрицательного» элемента

6. - существование «единичного» элемента

7. - существование «обратного» элемента

8. - ассоциативность умножения на скаляр

9. - дистрибутивность относительно вектора

10. - дистрибутивность относительно скаляра

Пример

Образует ли линейное пространство множество всех дифференцируемых функций a = f(t), b = g(t), если сумма задана – f(t) · g(t), произведение – α · f(t).

Попросту говоря, функция называется дифференцируемой, если её график можно нарисовать в виде непрерывной линии на всём участке.

Проверим выполнение всех свойств.

1. Произведение дифференцируемых функций, даст дифференцируемую функцию, произведение действительного числа на дифференцируемую функцию, также, даст дифференцируемую функцию.

2. Второе свойство выполняется по свойствам тождественных преобразований: от перестановки множителей произведение не меняется. Для дифференцируемых функций это также справедливо.

3. Свойство выполняется, аналогично предыдущему.

4. Нулевой элемент, т.к.. Функцияf(t) = 1 также дифференцируема, следовательно, нулевой элемент существует, свойство выполняется.

5. Отрицательный элемент для f(t): f '(t) = 1/f(t) существует, так как f(t) · 1/f(t) = 1 =. Однако, отрицательная функция f '(t) = 1/f(t) не всюду дифференцируемая, а только если f(t) не равно нулю. Следовательно, свойство не выполняется.

Дальнейшую проверку можно не проводить.

Ответ: не образует.

Примечание. В показанном примере, множество дифференцируемых функций образовывали бы линейное пространство, если сумма была бы определена следующим образом: f(t) + g(t).