5.7. Найти матрицу в базисе , где,,, если она задана в базисе:(0 2 1, 0 3 2, 1 1 -1)

Запишем вектора в виде системы и составим матрицу перехода и исходную матрицу.

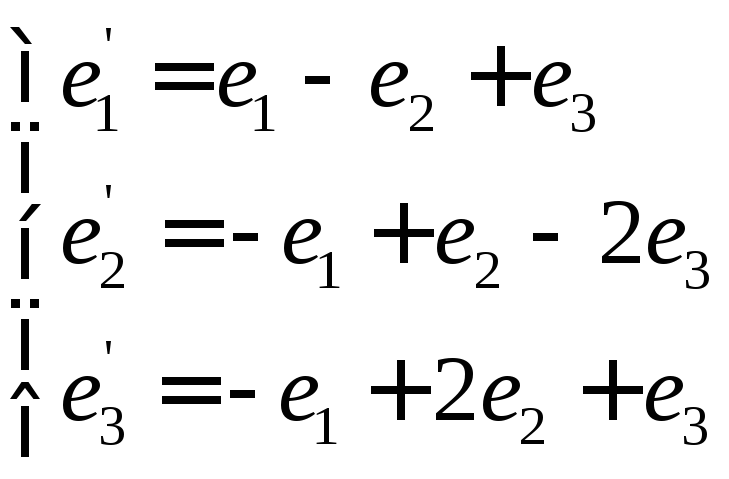
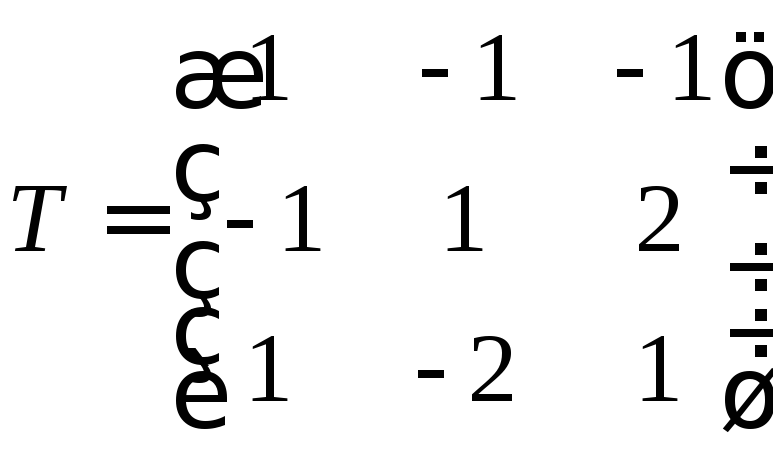
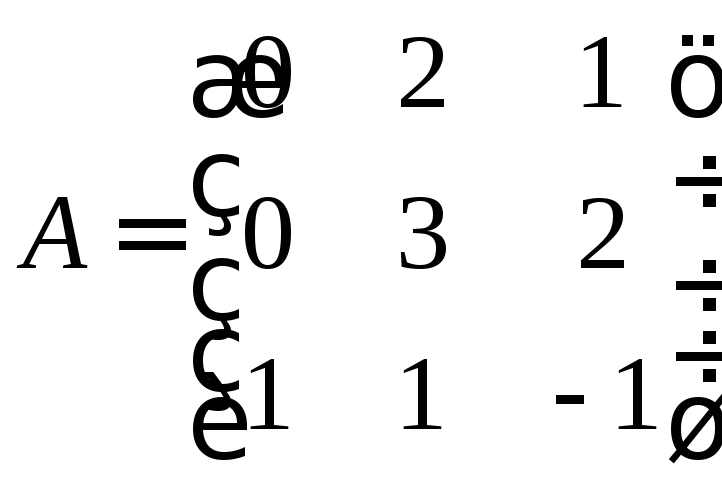
Воспользуемся формулой нахождения матрицы в новом базисе.

Найдем обратную матрицу и выполним произведение.

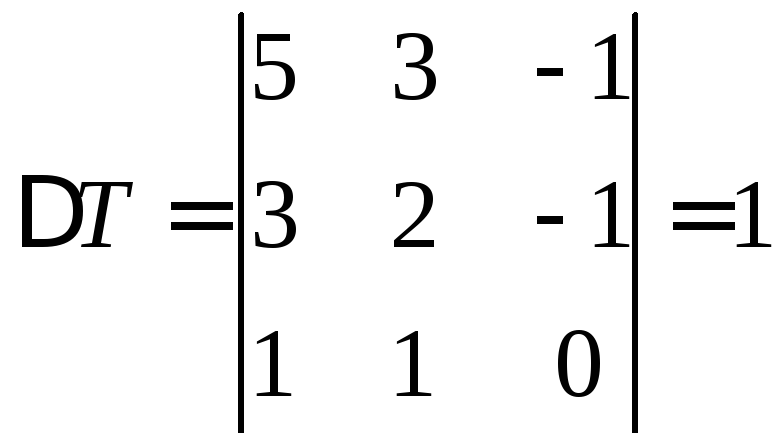
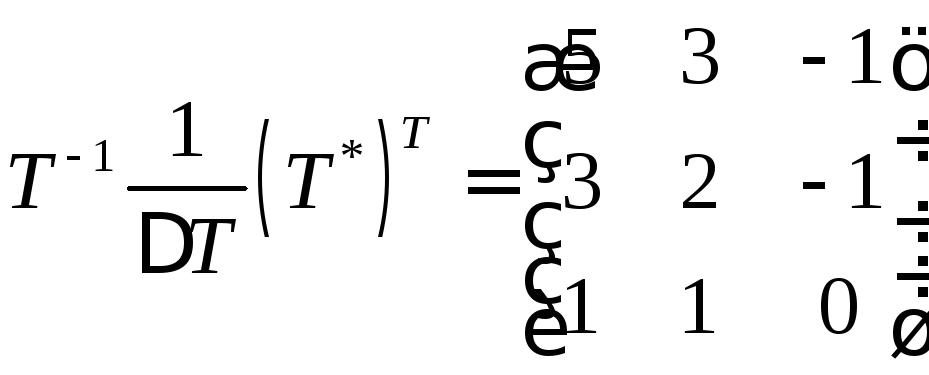
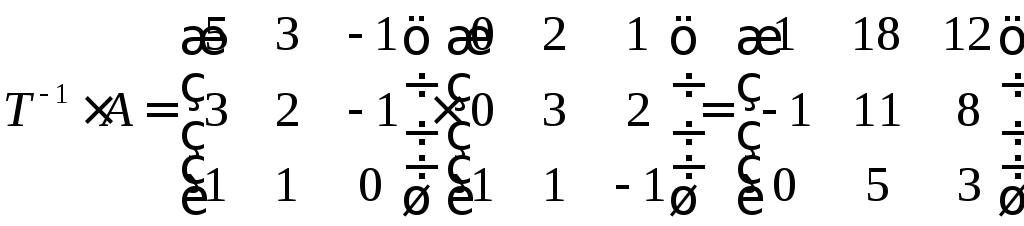
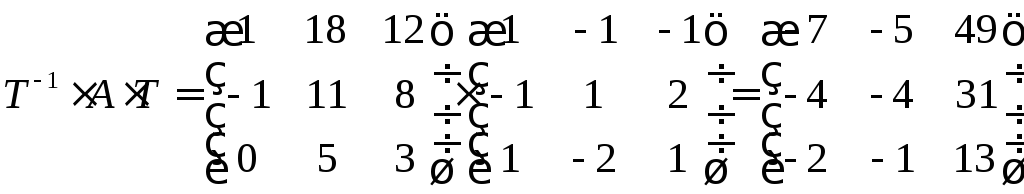
Ответ:

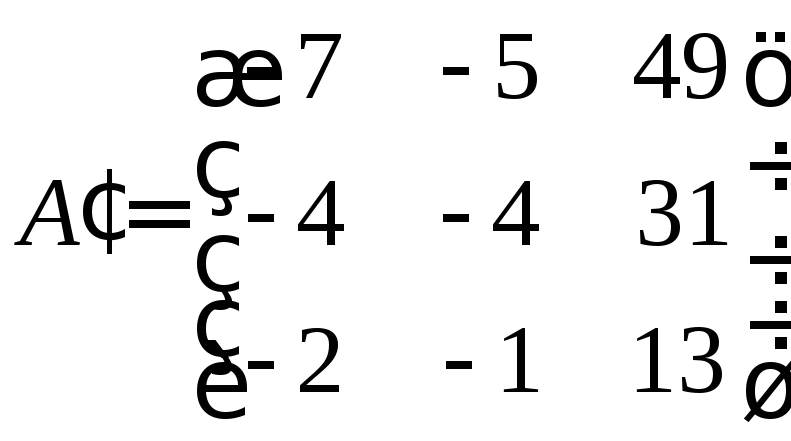
5.8. Доказать линейность, найти матрицу, область значений и ядро оператора проектирования на плоскость .

Нормальный вектор плоскости . Произвольная точка пространстваM(x, y, z) переходит в точку M₁(x₁, y₁, z₁). При этом вектор N является направляющим вектором прямой MM₁, поэтому канонические уравнения этой прямой будут:

.

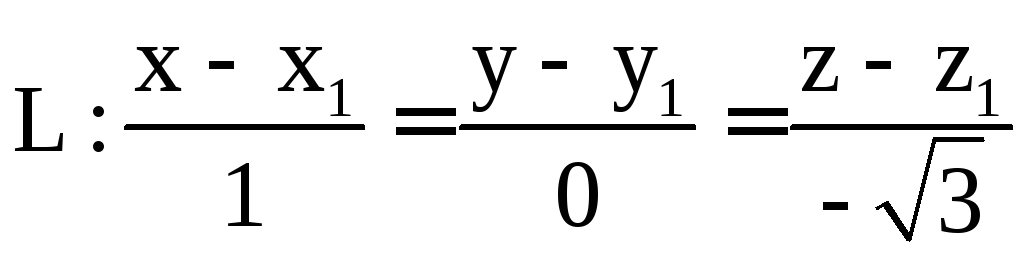Отсюда

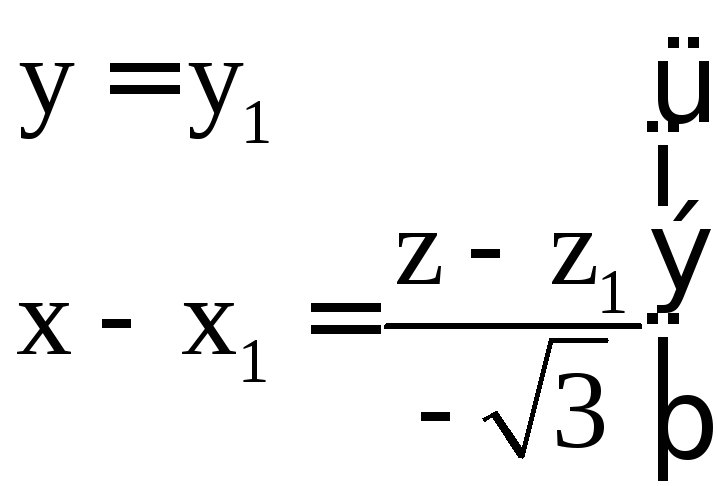
Точка М₁ одновременно принадлежит плоскости и прямойL, следовательно её координаты удовлетворяют уравнениям прямой и плоскости.

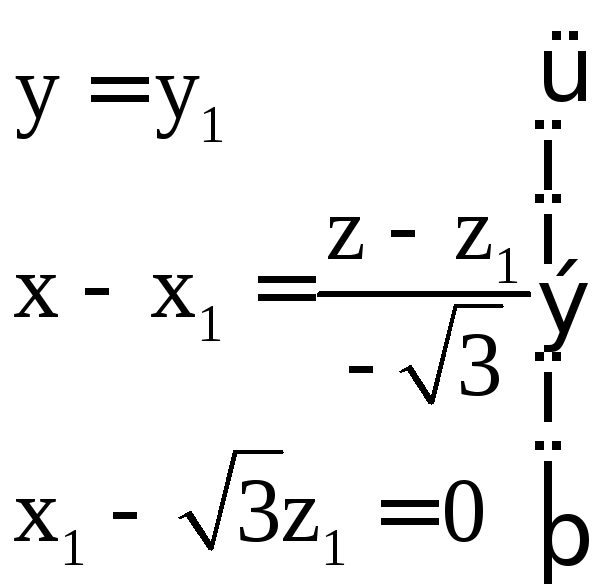
Преобразуем, чтоб найти координаты точки М₁.

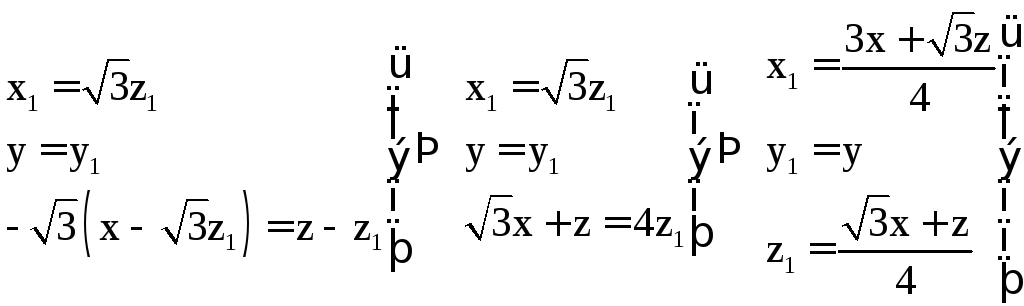
Мы получили координаты проекции, точка M(x, y, z) переходит в точку 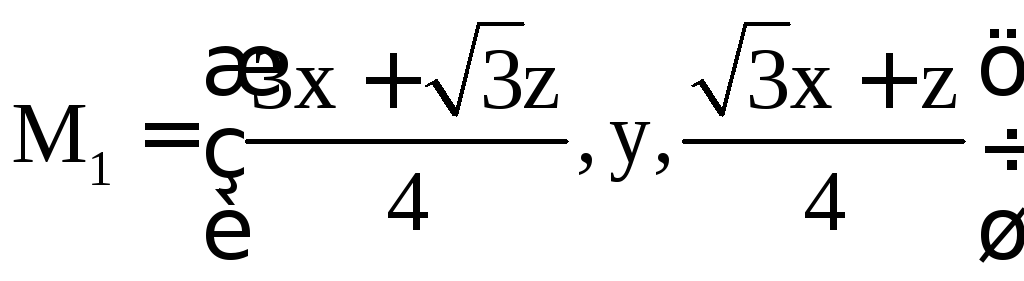, следовательно, проектирование на плоскостьвыполняется линейным преобразованием А.

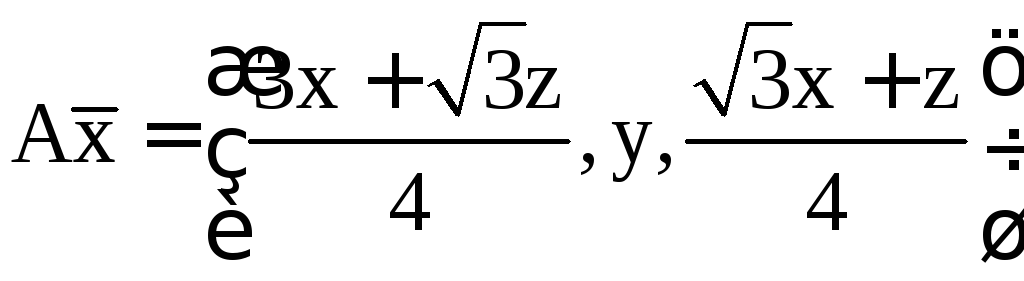
а) Проверим выполнение свойства .

Проверим линейность данного преобразования. Рассмотрим вектор и выполним над ним преобразование А.

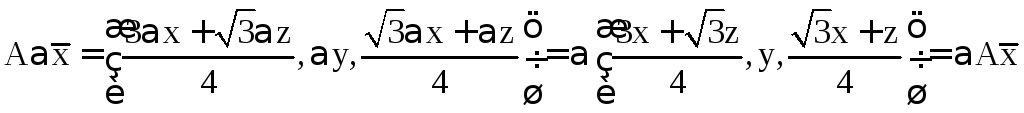
свойство выполняется.

б) Проверим выполнение свойства .

Выполним преобразование A над векторами.

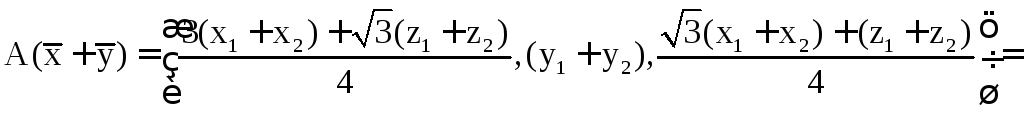
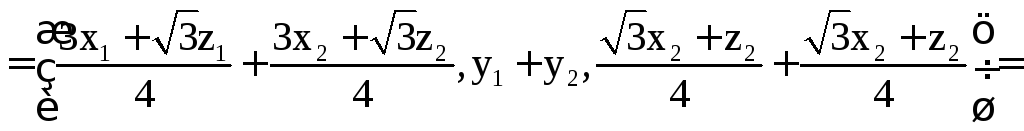
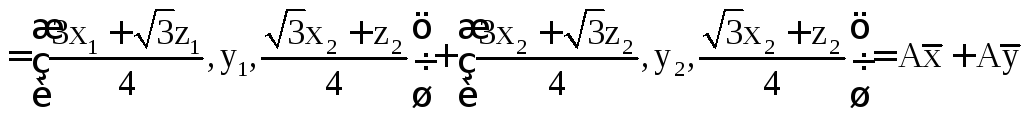
Оба свойства выполняются, значит, преобразование является линейным.

Составим матрицу преобразования. Для этого найдём образы орт:

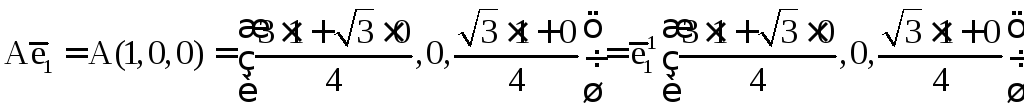
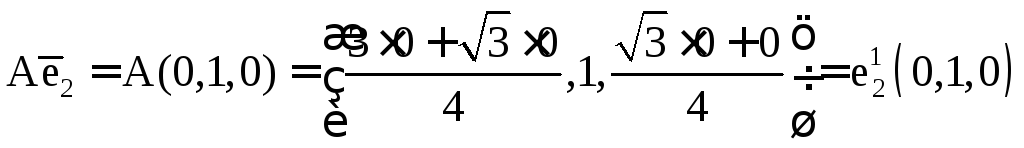
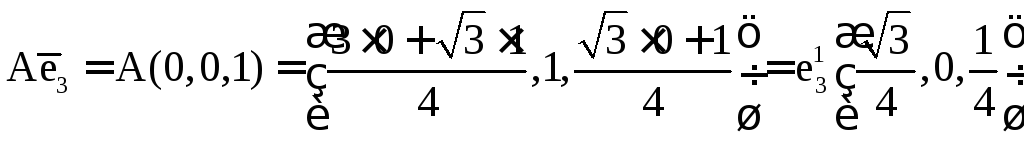
Построим матрицу линейного преобразования, строки в которой – координаты образов базисных векторов .

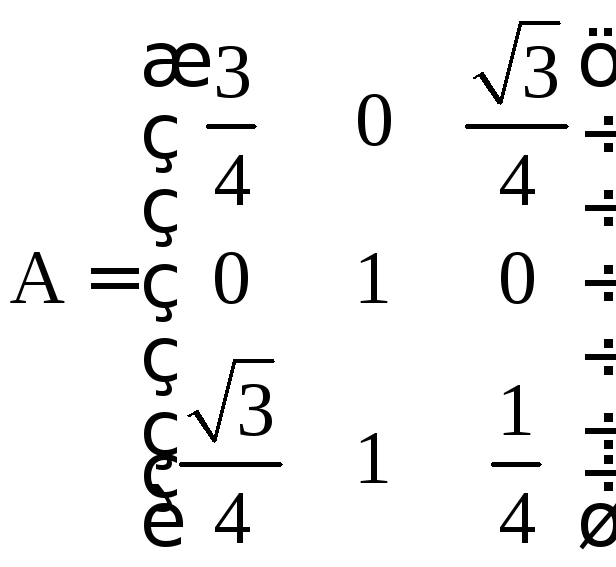
Областью значений преобразования А является множество всех образов этого преобразования, то есть .

Ядром линейного оператора является подпространство векторов, отображающихся в нулевой вектор

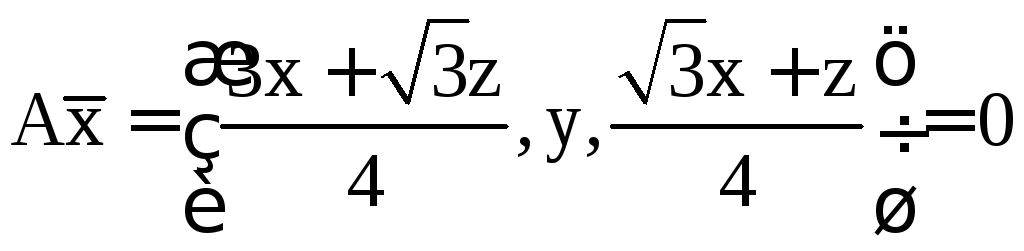
Распишем равенство по координатам и преобразуем

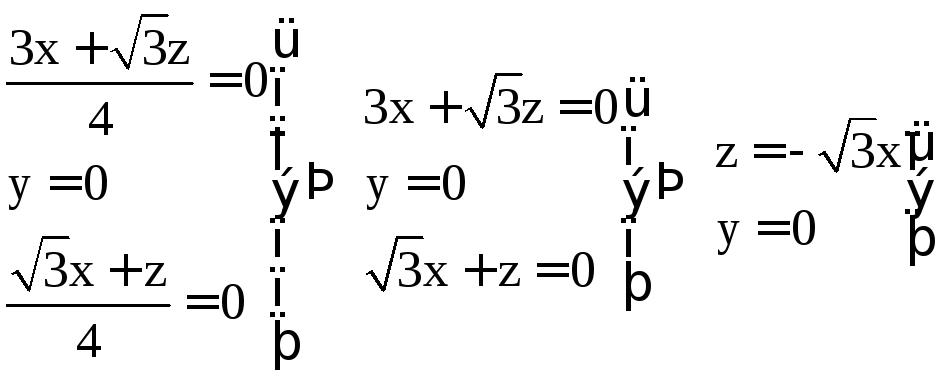
Запишем систему в виде канонических уравнений прямой

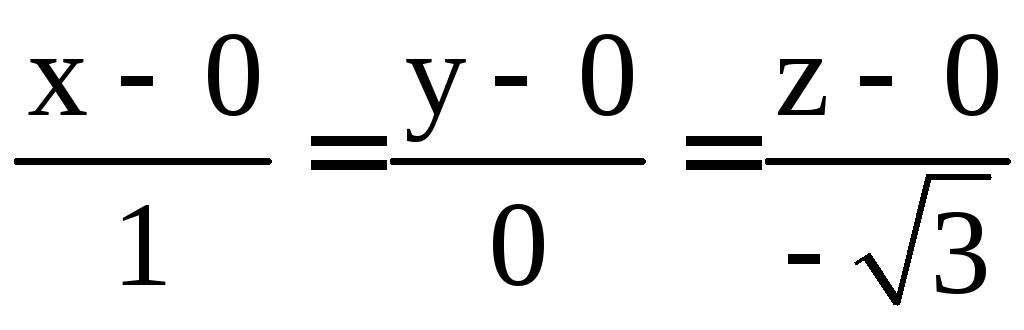
Это уравнение прямой, проходящей через начало координат и перпендикулярной к исходной плоскости .

Ответ: матрица 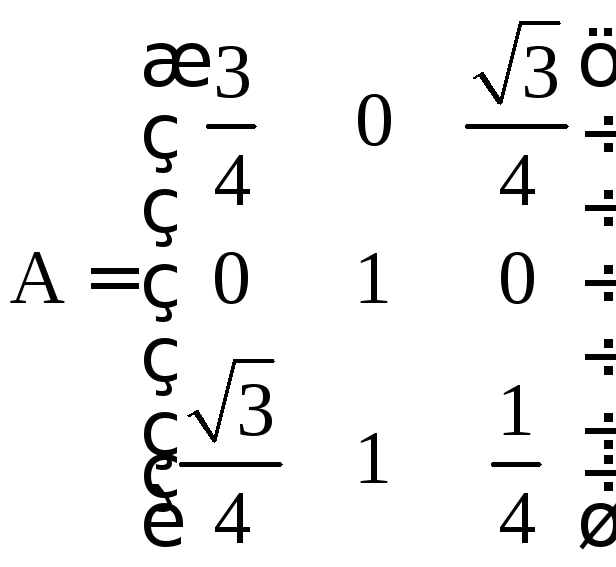, ядро линейного оператора.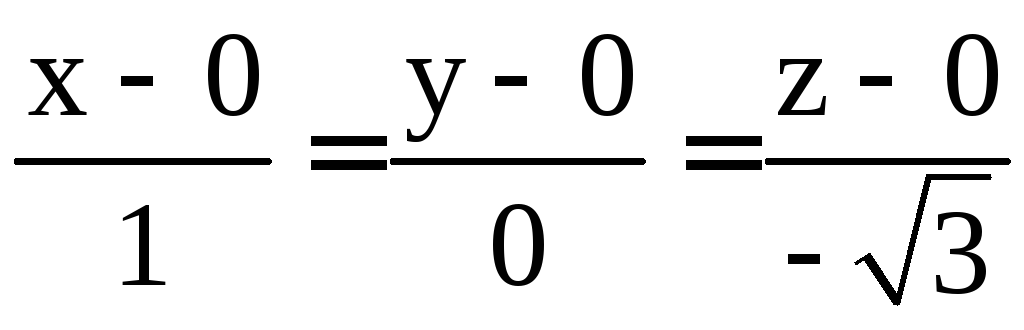

5.9. Найти собственные значения и собственные векторы матрицы

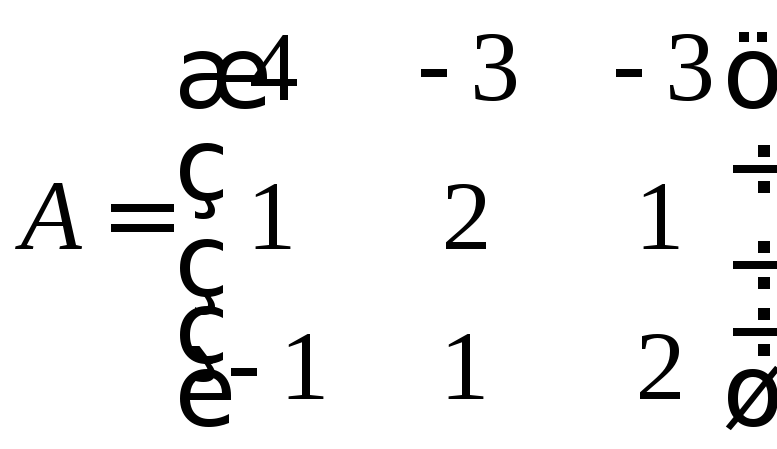
Собственные значения матрицы получим, решив характеристическое уравнение.

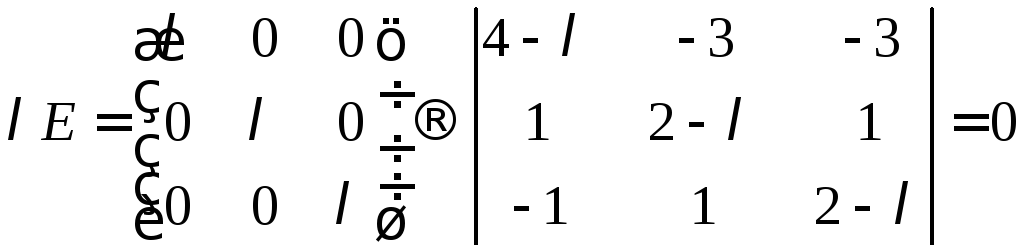
Раскроем определитель

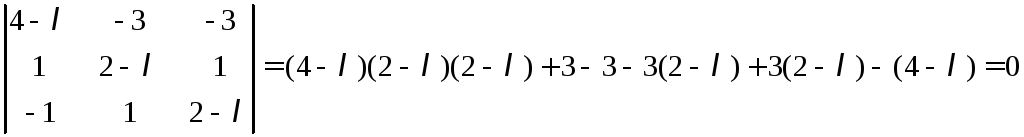
Решив данное уравнение любым способом, получим его корни:

Это и есть собственные значения матрицы.

Для нахождения собственных векторов матрицы, в выражение характеристического уравнения будем подставлять собственные значения.

:

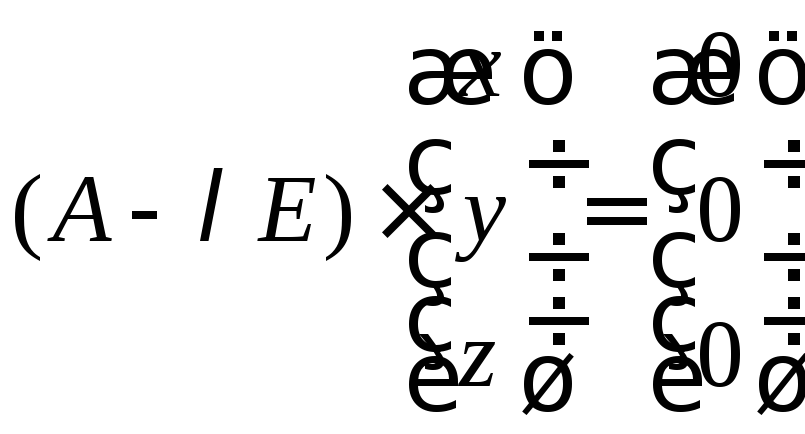
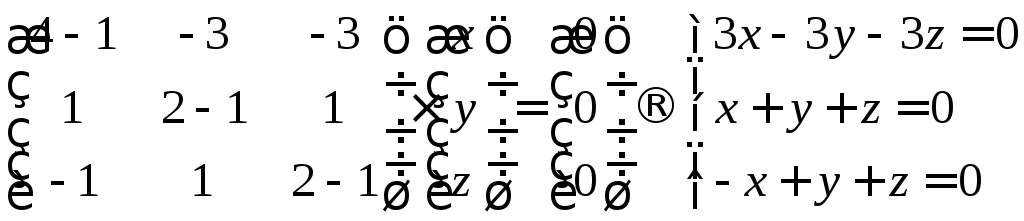
Решим систему методом Гаусса

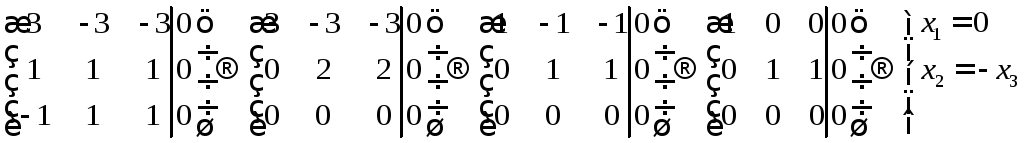
Получим собственный вектор .

Аналогично найдём и для других собственных значений.

:

:

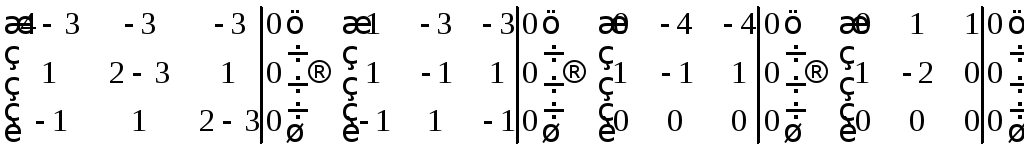
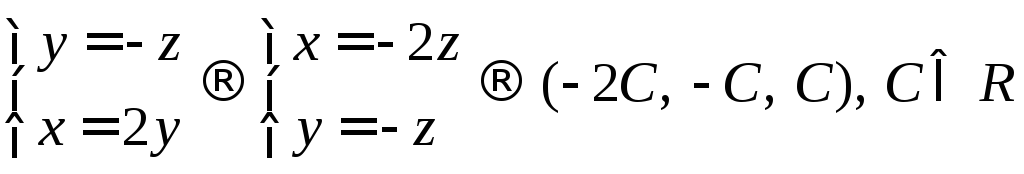
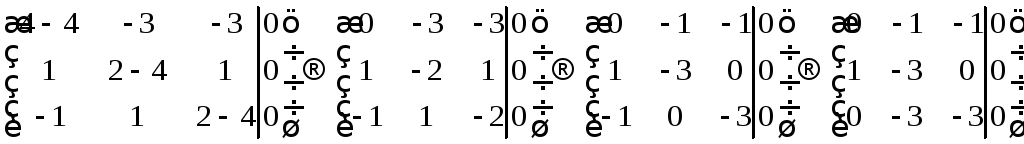
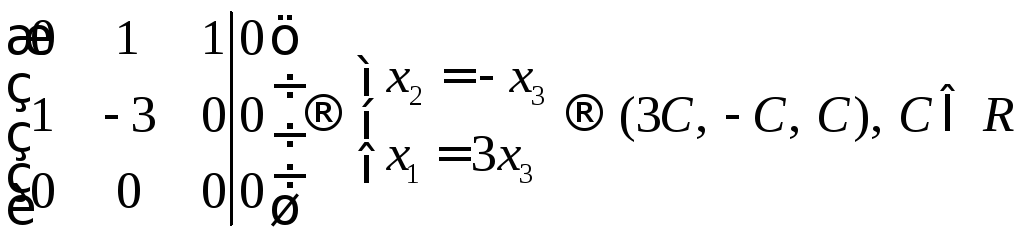
Ответ: собственные значения: 1, 3, 4; собственные вектора: (0, -C, C), (-2C, -C, C), (3C, -C, C).

6. Векторная алгебра

Даны четыре точки: A(1, -1, 2), B(2, 1, 0), C(-1, -2, 0), D(0, 1, 1)

6.1. Найти: .

Для нахождения координат вектора, необходимо из координат конечной точки почленно вычесть координаты начальной точки.

Имеются ли среди них коллинеарные?

Вектора коллинеарны в том случае, если отношение их координат равны

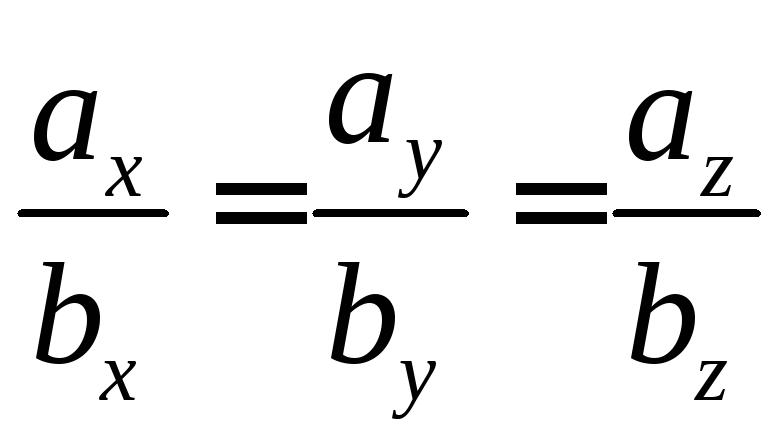
Проверим вектора a и b на коллинеарность

–не коллинеарны

Проверим вектора a и с на коллинеарность

–не коллинеарны

Если не коллинеаренине коллинеарен, значитне коллинеарентакже.

Ответ: ,,. Коллинеарных векторов нет.

Примечание. Вектор обозначается тремя координатами, это координаты конца вектора, а начало находится в начале координат (0, 0, 0). Т.к. по определению вектор – это направленный отрезок и не имеет относительного положения в пространстве.