
- •«Методичні вказівки і завдання для самостійної роботи при підготовці до модульного контролю з фізики (розділ «Електростатика. Постійний струм»)
- •«Методичні вказівки і завдання для самостійної роботи при підготовці до модульного контролю з фізики (розділ «Електростатика. Постійний струм»)
- •1.Робоча програма
- •2. Електростатика і постійний струм
- •3.Приклади розв’язання задач
- •4. Задачі
- •5. Питання для контролю знань
- •6.Таблиця відповідей на питання для контролю знань
- •7. Варіанти індивідуальних завдань
- •8.Додатки
- •8.1. Деякі основні фізичні сталі
- •8.2. Деякі астрономічні величини
- •8.3. Питомий електричний опір(при 200 с)
- •8.4. Ді електрична проникність
- •8.5. Температурний коефіцієнт(при20 0с)
- •8.6.Десяткові приставки до назв одиниць
- •8.7. Деякі позасистемні одиниці
- •9.Рекомендована література
3.Приклади розв’язання задач
Приклад 1. Плоский конденсатор площею пластин S і скляною пластинкою товщиною d заряджений до різниці потенціалів U і відключений від джерела напруги. Яку роботу потрібно виконати , щоб вийняти пластинку з конденсатора?
Дано: S,d,U,ε.
Визначити А.
Розв’язання . Роботу з видалення пластинки з конденсатора знаходимо як різницю початкової і кінцевої енергії зарядженого конденсатора.
![]() ,
,
де![]() -
- енергія конденсатора після видалення
пластинки;
-
- енергія конденсатора після видалення
пластинки;![]() - енергія конденсатора до видалення
пластинки.
- енергія конденсатора до видалення
пластинки.
Оскільки конденсатор отсоединен від джерела напруги, то заряд залишиться колишнім.
Виразимо енергію
конденсатора
![]() і
і![]() через заряд і ємність:
через заряд і ємність:
![]() ,
,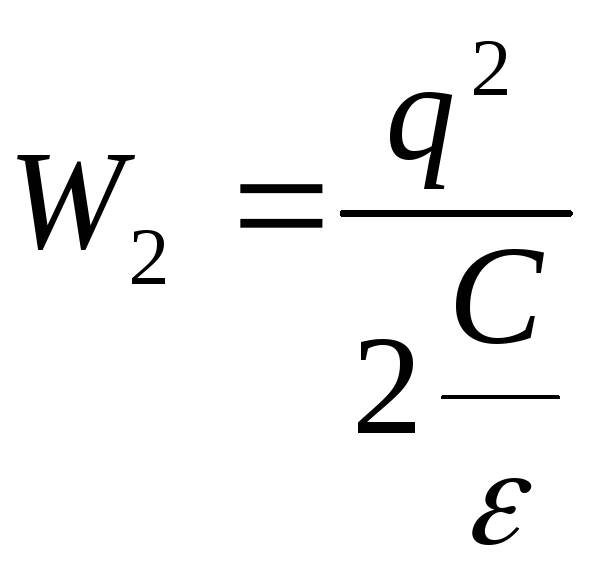 ,
,![]() .
.
Тоді
![]() тому що
тому що![]() ,
,
де ε - діелектрична проникність скла.
Перевіримо одиниці виміру А:
![]() .
.
Відповідь:
![]() .
.
Приклад 2. Генератор з ЕРС ε=140 В и внутрішнім опором r=0,2 Ом дає струм І=100А. Опір зовнішнього кола R=1,2 Ом. Визначити повну і корисну потужність генератора, втрати потужності і ККД. Скласти рівняння балансу потужностей.
Дано: ε =140 В, r=0.2 Ом, І=100A, R=1,2 Ом.
Визначити:
![]() ;
P;ΔP
і ККД.
;
P;ΔP
і ККД.
Розв’язання. Повна потужність генератора:
![]() ,
(1)
,
(1)
де І - сила струму; ε - ЕРС.
Корисна потужність:
![]() ,
(2)
,
(2)
де U - різниця потенціалів на кінцях ділянки кола.
Враховуючи , що
![]() ,
(3)
,
(3)
де r - внутрішній опір джерела струму
маємо:
![]() .
(4)
.
(4)
Втрати потужності в зовнішньому колі
![]() .
(5)
.
(5)
ККД:
![]() .
(6)
.
(6)
Перевіримо одиниці виміру шуканих величин:
![]() ;
;
![]() ;
;
![]() .
.
Підставляючи в (1,4,5 і 6) числові значення й обчислюючи, одержимо:
![]() Вт=14 (кВт);
Вт=14 (кВт);
![]() (Вт)=12 (кВт);
(Вт)=12 (кВт);
ΔP=14-12=2 (кВт);
![]() .
.
Перевіримо рівняння балансу потужностей:
![]() ;
;
140.100=10000.0,2+10000.1,2 ;
14000Вт =14000Вт.
Відповідь:
![]() = 14 кВт;
P = 12 кВт; ΔP=2
кВт; η=85,7%.
= 14 кВт;
P = 12 кВт; ΔP=2
кВт; η=85,7%.
Приклад
3. Сила
струму в провіднику опором R=50 Ом
рівномірно росте від I0
=0 доImax
=3А за час![]()
![]() =6 c. Визначити кількість теплоти , що
виділилася в провіднику за цей час.
=6 c. Визначити кількість теплоти , що
виділилася в провіднику за цей час.
Дано: R=50
Ом ;
![]() ;
;
![]() ;
τ=6 c.
;
τ=6 c.
Визначити Q.
Розв’язання. Відповідно до закону Джоуля-Ленца у випадку нескінченно малого проміжку часу
![]() .
.
За умовою задачі сила струму рівномірно росте, тобто
![]() ,
,
де коефіцієнт
пропорційності![]() .
.
Тоді можна записати:
![]() . (1)
. (1)
Після інтегрування (1) з урахуванням виразу для K, одержимо:
![]() .
(2)
.
(2)
Перевіримо одиниці виміру Q:
![]()
Підставивши в (2) числові значення й обчислюючи , одержимо:
![]() .
.
Відповідь: Q=900 Дж.
Приклад 4.
Густина електричного струму в мідному
проводі дорівнює 10![]() . Визначити питому теплову потужність
струму, якщо питомий опір міді
. Визначити питому теплову потужність
струму, якщо питомий опір міді![]()
Дано:
![]() ;
;
![]() .
.
Визначити: ω.
Розв’язання . Відповідно до законів Джоуля-Ленца й Ома в диференціальній формі,
![]() ,
(1)
,
(1)![]()
![]() ,
(2)
,
(2)
де γ і ρ - відповідно питомі провідність і опір провідника;
E - напруженість електричного поля;
ω - питома теплова потужність струму.
З закону (2) одержимо, що E= ρ γ. Підставивши цей вираз в (1), знайдемо шукану величину теплової потужності струму.
ω
=![]() ј2=ј2ρ
. (3)
ј2=ј2ρ
. (3)
Перевіримо одиниці виміру:
[ω]
=![]() .
.
Підставивши в (3) числові значення й обчислюючи , одержимо:
![]() .
.
Відповідь:
![]() .
.
Приклад 5. Між обкладками плоского конденсатора, зарядженого до різниці потенціалів 1,5 кВ, затиснута парафінова пластинка (ε=2) товщиною 5 мм.
Визначити поверхневу густину зв'язаних зарядів на парафіні.
Дано: U=1,5кВ=1,5 В; ε
= 2; d = 5мм =![]() м.
м.
Визначити![]() .
.
Розв'зання .
Тому що вектори
![]() і
і![]() нормальні до поверхні діелектрика, то
нормальні до поверхні діелектрика, то![]()
![]() ;
;![]() .
.
Тоді можна записати
![]() ,
(1)
,
(1)
де
![]() і
і![]() -
відповідно вектори електричного
зміщення і напруженості поля плоского
конденсатора;
-
відповідно вектори електричного
зміщення і напруженості поля плоского
конденсатора;
![]() - вектор
поляризованності діелектрика. P =
- вектор
поляризованності діелектрика. P =
![]() ,
тобто дорівнює поверхневій густині
зв'язаних зарядів діелектрика.
,
тобто дорівнює поверхневій густині
зв'язаних зарядів діелектрика.
Тоді
![]() .
.
Звідси
![]() .
(2)
.
(2)
З огляду на те, що
![]() і
і![]() ,
,
де d - відстань між обкладками конденсатора, одержимо:
![]() .
(3)
.
(3)
Перевіримо одиниці
виміру![]() :
:
![]() .
.
Підставивши в (3) числові значення й обчислюючи , одержимо:
![]() .
.
Відповідь:
![]() .
.
Приклад 6.
Відстань l між двома точковими зарядами
![]() =1нКл
і
=1нКл
і![]() =-2нКл,
розташованими у вакуумі, дорівнює 10 см.
Визначити:
=-2нКл,
розташованими у вакуумі, дорівнює 10 см.
Визначити:
1)Напруженість E;
2)Потенціал φ поля,
створюваного цими зарядами в точці А,
віддаленій від першого заряду на відстань
![]() = 9 см і від другого заряду на
= 9 см і від другого заряду на![]() =7см.
=7см.
Дано: l=10 см = 0.1 м;
![]() =1нкл= Кл;
=1нкл= Кл;![]() =-2нкл=
=-2нкл=![]() Кл;
Кл;
![]() =9
см
=0,09 м;
=9
см
=0,09 м;
![]() =7
см=0,07 м.
=7
см=0,07 м.
Визначити: 1)Е; 2) φ.
Розв’язання.
Відповідно до принципу суперпозиції
![]() .
.
Напрями векторів зазначені на рис.1. Модуль вектора знайдемо за теоремою косинусів:
Рис.3.1.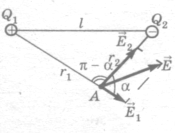
![]() ,
(1)
,
(1)
де ![]() .
(2)
.
(2)
У даному випадку, щоб уникнути громіздких записів, зручно значення cos α обчислити окремо:
![]() .
(3)
.
(3)
Напруженості
електричного поля, створювані у вакуумі
зарядами![]() і
і![]() :
:
![]() ,
,
![]() .
(4)
.
(4)
Підставивши (4) і (3) у формулу (1), одержимо шукану напруженість:
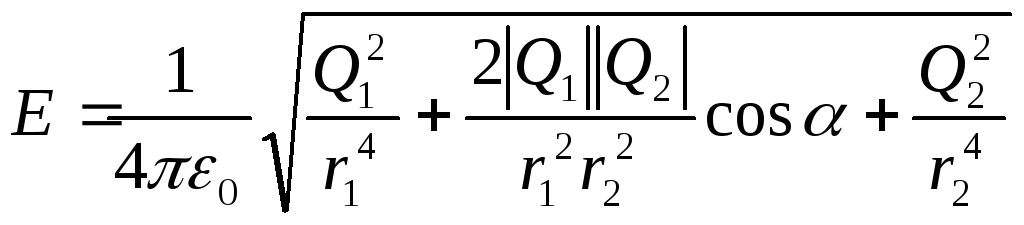 .
(5)
.
(5)
Відповідно до принципу суперпозиції, потенціал результативного поля
![]() ,
(6)
,
(6)
де![]() і
і![]() - потенціали полів створюваних
відповідно
- потенціали полів створюваних
відповідно
зарядами
![]() і
і![]() .
.
Тоді
![]() .
(7)
.
(7)
Перевіримо одиниці виміру Е і φ :
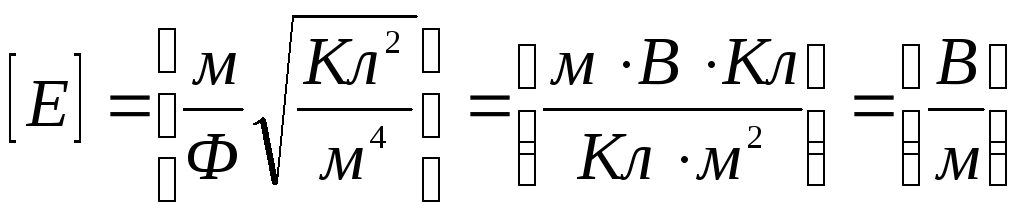 ;
;
![]() .
.
Підставивши в (5)
і (7) числові значення й обчислюючи ,
одержимо:
![]()

![]() .
.
Відповідь: E=3,57 кВ/м; φ=-157 В.
П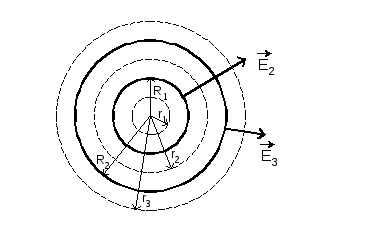 риклад
7.Дві
концентричні провідні сфери радіусами
R1=6
см і R2=10см
несуть відповідно заряди Q1=1
нКл і Q2=-0.5
нКл. Знайти напруженість поля в точках,
що відстоять від центра
сфер на
відстанях r1=5
см, r2=9
см і
риклад
7.Дві
концентричні провідні сфери радіусами
R1=6
см і R2=10см
несуть відповідно заряди Q1=1
нКл і Q2=-0.5
нКл. Знайти напруженість поля в точках,
що відстоять від центра
сфер на
відстанях r1=5
см, r2=9
см і
r3=15см. Побудувати графік E(r).
Дано: R1=0.06 м, R2=0.1 м, Q1=10-9 Кл,
Q2=-5*10-10 Кл, r1=5*10-2 м, r2=9*10-2 м, Рис.3.2
r3=15*10-2 м.
Визначити:Е1;Е2;Е3;Е(r).
Розв’язання .
Для визначення напруженості Е1 проведемо гауссову поверхню S1 Рис.3.2
радіусом r 1, рис.3.2 і скористаємося
теоремою Остроградського-Гаусса :
![]()
(тому що сумарний заряд, що знаходиться усередині гауссової поверхні,дорівнює нулю).
Отже,
![]() і Е1
у всіх точках, що задовольняють умові
r1<R1,
буде дорівнювати нулю.
і Е1
у всіх точках, що задовольняють умові
r1<R1,
буде дорівнювати нулю.
2. Проведемо гауссову поверхню радіусом r2.
(тому що усередині гауссової поверхні знаходиться тільки заряд Q1).
З розумінь симетрії En=E2=const, тому Е2 можна винести за знак інтеграла:
![]() або
,
або
,
![]()
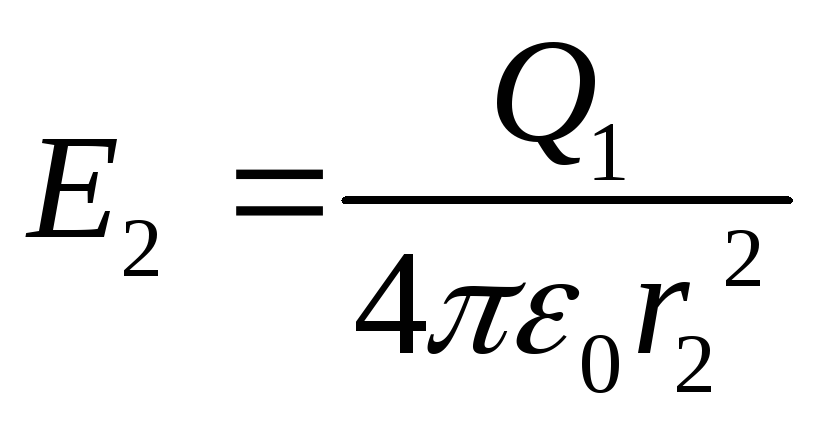 ,
,
д е
е![]() -
-
площа гауссової поверхні.
3.Проведемо гауссо-
ву поверхню радіусом r3.
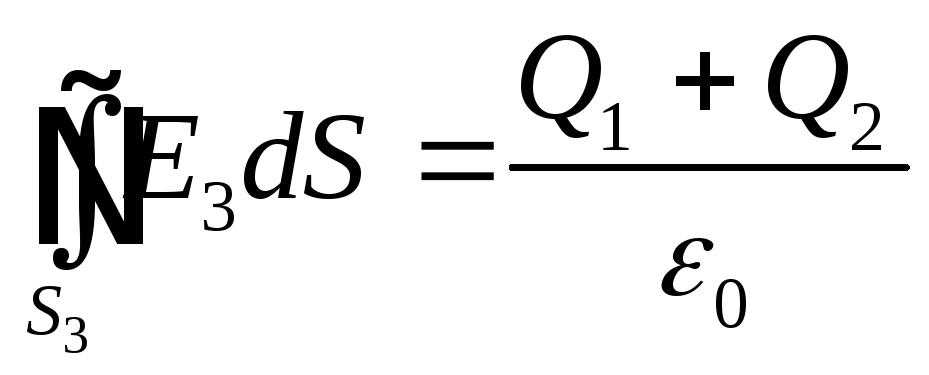
(тому що усередині гауссової поверхні Рис.3.3
знаходяться заряди Q1 і Q2).
![]() - площа гауссової
поверхні.
- площа гауссової
поверхні.
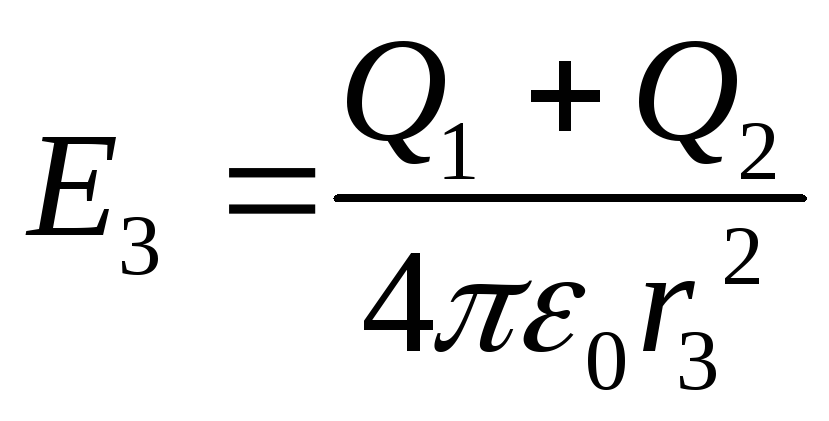 .
.
Перевіремо одиниці вимірювання Е.
![]()
Підставивши числові значення і обчислюючи , одержимо:
![]() ;
;
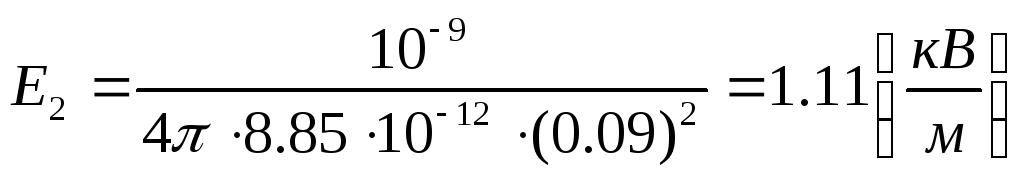 ;
;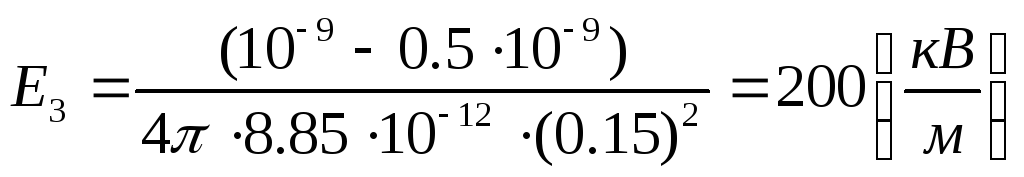 .
.
Побудуємо графік E(r),
1) r<R1, Е1=0
2) r=R,
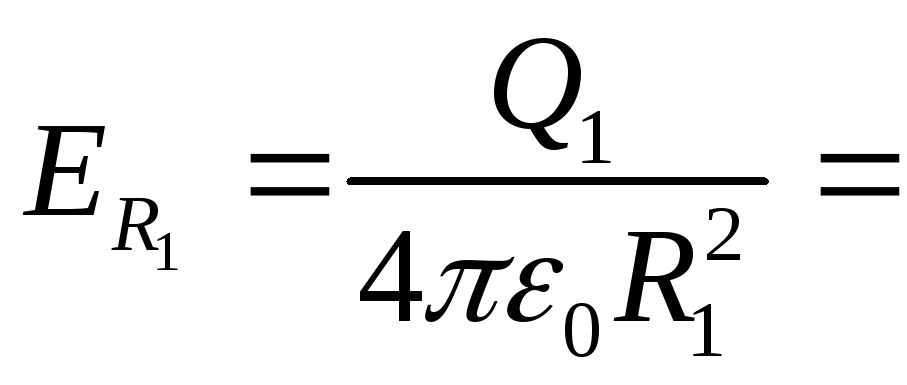
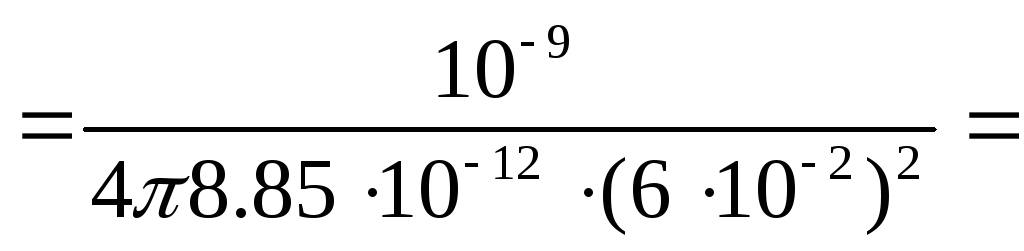
![]() .
.
E2(r)
змінюється за законом
![]() .
.
r=R2;
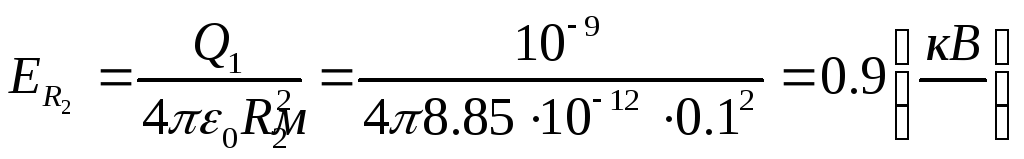 ;
;
3) r
=R2;
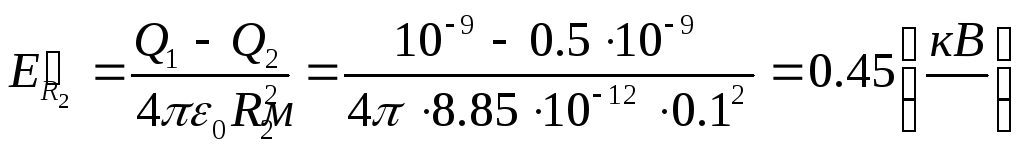 .
.
Таким чином, функція E(r) у точках r=R1 і r=R2 терпить розрив.
Відповідь: Е1=0;
Е2=1.11![]() ;
Е3=200
;
Е3=200![]() .
.
.
Приклад 8.
На відстані![]() =4см
від нескінченно довгої зарядженої нитки
знаходиться точковий заряд q=0,66 нКл. Під
дією поля заряд наближається до нитки
до відстані
=4см
від нескінченно довгої зарядженої нитки
знаходиться точковий заряд q=0,66 нКл. Під
дією поля заряд наближається до нитки
до відстані
![]() =2
см. При цьому виконується робота
=2
см. При цьому виконується робота![]() Дж. Знайти лінійну густину заряду на
нитці.
Дж. Знайти лінійну густину заряду на
нитці.
Дано:
![]() = 4см=
= 4см=![]() м;
м;![]() =2
см=
=2
см=![]() м;
q=0,66нКл;
м;
q=0,66нКл;
А=![]() Дж
Дж
Визначити: τ
Розв’язання .
Робота сили электричного поля при переміщенні заряду
![]() ,
,
де dU=-E dr;
![]() -
напруженість поля нескінченно довгої
зарядженої нитки.
-
напруженість поля нескінченно довгої
зарядженої нитки.
Тоді
![]()
Проінтегрувавши це рівняння , одержимо:

Звідси

Перевіримо одиниці виміру τ:
![]()
Підставивши числові значення й обчислюючи , одержимо:
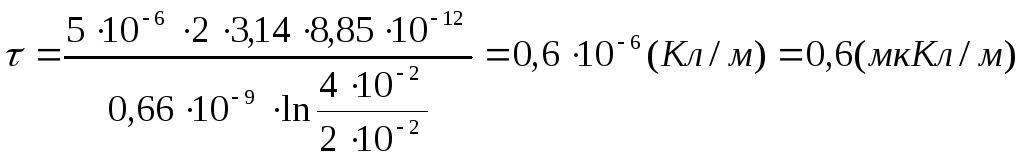 .
.
Відповідь:
![]() .
.
.
Приклад 9. На тонкому стрижні довжиною l=20 см знаходиться рівномірно розподілений електричний заряд. На продовженні осі стрижня на відстані а=10 см від найближчого кінця знаходиться точковий заряд Q1 =40 нКл, що взаємодіє зі стрижнем із силою
F=6 мкН. Визначити лінійну густину заряду на стрижні.
Дано: l=0,2 м; а=0,1
м; Q1=40нКл=4
![]() Кл.
Кл.
Визначити: τ.
Розв’язання .
Відповідно до закону Кулона сила взаємодії двох точкових зарядів
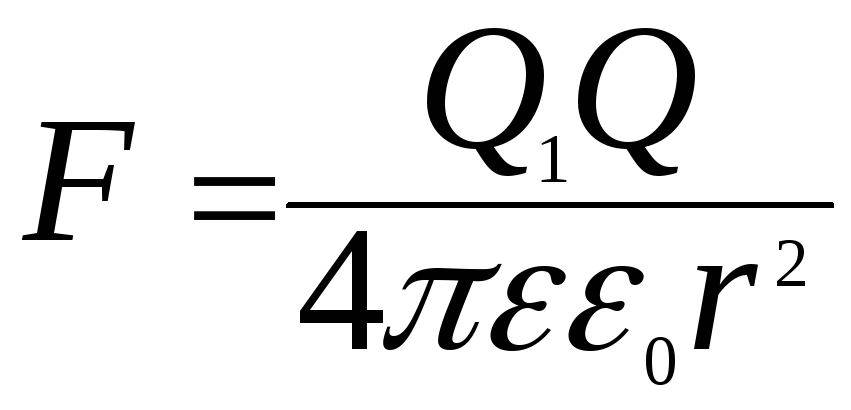 ,
,
де ε =1 - діелектрична проникність середовища,
ε![]() - електрична стала,
- електрична стала,
r - відстань між зарядами.
Заряд на стрижні не є точковим, тому на стрижні рис.4 виділимо малу ділянку dr з зарядом dQ= τdr , де τ- лінійна густина заряду на стрижні.
Одержимо:
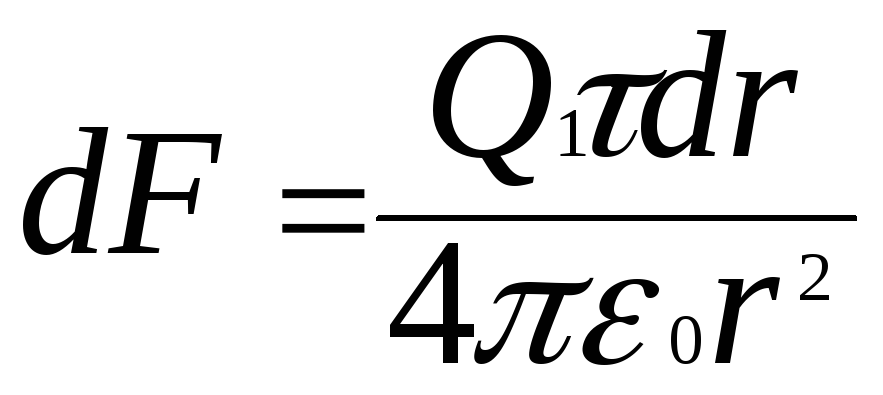 . (1)
. (1)
Інтегруючи (1) в межах від а до а+l , одержимо
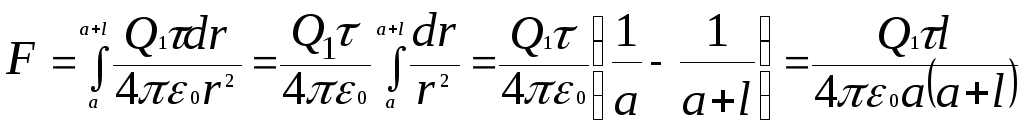 .
.
d r
r
r
r
• Q1
І a
Рис.3.4
Відкіля:
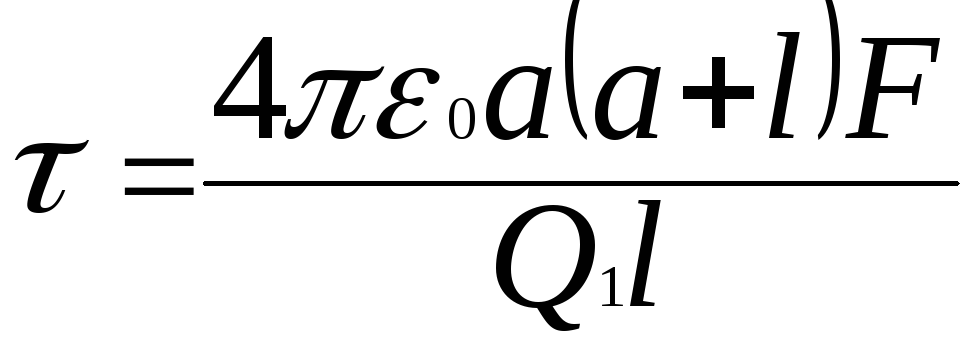 .
.
Перевіримо одиниці вимірювання:
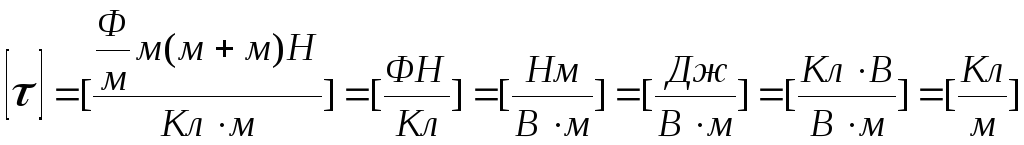 .
.
Підставивши числові значення й обчислюючи, одержимо:
![]() .
.
Відповідь:
![]() .
.
Приклад 10.
Визначити силу струму, що тече через
елемент ε![]() ,
,
якщо ε![]() = 1В, ε
= 1В, ε![]() = 2 В, ε
= 2 В, ε![]() = 3 В,r
= 3 В,r![]() = 1 Ом,r
= 1 Ом,r![]() = 0.5 Ом,r
= 0.5 Ом,r![]() = 1/3 Ом,
= 1/3 Ом,
R![]() = 1 Ом,R
= 1 Ом,R![]() = 1/3 Ом.Дано: ε
= 1/3 Ом.Дано: ε![]() = 1 В; ε
= 1 В; ε![]() = 2 В; ε
= 2 В; ε![]() = 3 В;r
= 3 В;r![]() = 1 Ом;r
= 1 Ом;r![]() = 0.5 Ом;r
= 0.5 Ом;r![]() = 1/3 Ом;R
= 1/3 Ом;R![]() = 1 Ом;R
= 1 Ом;R![]() = 1/3 Ом.
= 1/3 Ом.
Визначити І2 .
 B
I1
ε1 ,
r1
C
B
I1
ε1 ,
r1
C
I3
R4 I2 ε2,r2 ε3 , r3
А R5 Д
Рис.3.5
Розв’язання .
Виберемо довільно напрями струмів у кожній ділянці кола (див. рис .5 ). На рис.5 ці напрями показано стрілками .Щоб визначити силу струму І2 , застосуємо закони Кірхгофа.
За першим законом Кірхгофа для вузла А маємо :
– I![]() +
I
+
I![]() +
I
+
I![]() = 0.
(1)
= 0.
(1)
Запишемо другий закон Кірхгофа для контуру АВСА
– I![]() r
r![]() –
I
–
I![]() R
R![]() –
I
–
I![]() r
r![]() =
ε
=
ε![]() –
ε
–
ε![]() ;
(2)
;
(2)
для контуру ADCA
I![]() r
r![]() –
I
–
I![]() R
R![]() – I
– I![]() r
r![]() =
ε
=
ε![]() –
ε
–
ε![]() ; (3)
; (3)
Підставивши в (2) і (3) числові значення опорів і ЕРС, одержимо систему рівнянь:
І
I![]() =
I
=
I![]() +
I
+
I![]() ;
(4)
;
(4)
2I![]() +
0.5I
+
0.5I![]() = 1 ;
(5)
= 1 ;
(5)
– 0.5I![]() +
2/3I
+
2/3I![]() =
1.
(6)
=
1.
(6)
Із (4) і (5) дістанемо:
0.5I![]() + 2I
+ 2I![]() + 2I
+ 2I![]() = 1,
= 1,
I![]() =
=
![]() .
.
Із
(6) і (7)
знайдемо
I![]() .
.
– 0.5I![]() +
+
![]()
![]() =1 чи
=1 чи
– 1.5
I![]() +
1 – 2.5
I
+
1 – 2.5
I![]() = 3
.
= 3
.
Звідси І2 = - 1/2 А.
Знак мінус у числового значення сили струму І2 свідчить про те, що при довіль-ному виборі напрямів струмів, зазначених на рис.5 , напрям струму І2 було зазначено протилежно дійсному . Насправді струм І2 тече від вузла A до С.
Відповідь: І = - 1/2 A.
Начало формы
Приклад 11. Скільки витків ніхромового дроту діаметром d = 1мм треба намо-тати на фарфоровий циліндр радіусом а = 2,5 см, щоб отримати піч опором R = 40 Ом?Дано: d = 1мм; а = 2,5 см; R = 40 Ом. Визначити N.
Рішення.
Опір провідника можна розрахувати за
формулою
![]() (I),
(I),
де - питомий опір (для ніхрому = 1мк0м.м), l - довжина провідника,
S -
площа його поперечного перерізу. Довжина
одного витка дорівнює 2![]() ,
тоді довжина всього дроту l=
N 2
,
тоді довжина всього дроту l=
N 2![]() —
(2),де
N
-
кількість витків. Площа поперечного
перерізу
—
(2),де
N
-
кількість витків. Площа поперечного
перерізу
![]()
Підставивши (3) і (2) в (I), отримаємо
![]() ;
звідки
;
звідки
![]() ;
;
Перевіримо одиниці вимірювань
![]() .
N
одиниць вимірювань не має.
Підставивши
числові значення та обчислюючи отримаємо:
.
N
одиниць вимірювань не має.
Підставивши
числові значення та обчислюючи отримаємо:
![]() =200
=200
Відповідь N = 200.
Приклад
12.Реостат
із залізного дроту, амперметр і генератор
включені послідовно. При t0
= 0
0 С
опір реостата R0
=
120 Ом,
опір амперметра RAO
=
20 Ом.
Амперметр показує струм I0
= 22 мА.
Який струм буде показувати амперметр,
якщо реостат нагріється на
![]() T
=50К. Температурний коефіцієнт опору
заліза α = 6.10-3К-1?
T
=50К. Температурний коефіцієнт опору
заліза α = 6.10-3К-1?
Дано:
t0
=
00С;
R0
= 120 Ом; RAO
= 20 Ом; I0
= 22 мА;
![]() T
= 50 К;
T
= 50 К;
α = 6.10-3К-1.
Визначити I.
Рішення.
Запишемо закон Ома для початкового
стану кола:
![]() .
(1)
.
(1)
Після нагрівання реостата його опір R0 змінилося і стало R.Амперметр став показувати ток
![]() .
(2)
.
(2)
Опір реостата можна знайти за формулою
![]() .
(3)
.
(3)
Питомий опір залежить від температури таким чином:
![]() .
(4)
.
(4)
В початковому стані
![]() ,
,
звідки
![]() . (5)
. (5)
Підставивши (4) і (5) в (3), отримаємо
![]() .
(6)
.
(6)
З (1) знайдемо
![]() (7)
(7)
Підставивши (6) і (7) в (2), знайдемо
![]() .
.
Підставивши числові значення та обчислюючи,отримаємо:
![]() =17,5.10-3(А).
=17,5.10-3(А).
Відповідь I = 17,5.10-3 (А).
