3.2. Векторы и линейные операции над ними

Займемся теперь изучением векторов в евклидовых пространствах и(на плоскости и в  пространстве) и операций над ними. В рамках этой главы подвекторными величинами (векторами)  будем понимать направленные  отрезки. Например, скорость, сила, ускорение являются векторными величинами.

 Скалярными величинами (скалярами)  будем называть величины, которые полностью определены своим числовым значением. Например, длина, площадь, объем, масса, температура.

Заметим, что когда векторы рассматриваются на плоскости или в пространстве, то подчеркивая их связь с направленным отрезком над буквами, их обозначающими, часто ставится черточка. Мы здесь не будем этому следовать исключительно из-за технических сложностей, связанных с набором такого текста. Для обозначения векторов будем использовать курсив:  a, b, c,... . 

Если началом вектора является точка  A, а концом - точка B, и нам надо указать это, то обозначать его будем так же, как это делается для направленных отрезков: .

Расстояние между началом и концом вектора называется его  длиной (а также модулем или абсолютной величиной).  Длина вектора обозначается │ или.

Векторы называются  коллинеарными, если они расположены на одной прямой или на параллельных прямых. Векторы называются  компланарными , если они параллельны некоторой плоскости.

Нулевой вектор считается коллинеарным любому вектору, так как он не имеет определенного направления.

Два вектора называются равными,  если они коллинеарные, одинаково направлены и равны по длине.

К линейным операциям над векторами относятся сложение, вычитание и умножение на число. Пусть и- два произвольных вектора. Путем параллельного переноса совместим начало векторас концом вектора.

Вектор, соединяющий начало вектора  с концом вектора, называетсясуммой векторов и обозначается

Рис.3.7. Правила сложения векторов: а) правило треугольника,

б) правило многоугольника, в) правило параллелограмма.

Это правило построения суммы называется  правилом треугольника (рис. 3.7а). Сумма нескольких векторов строится по правилу многоугольника (рис.3.7б): предварительно совмещают начало каждого последующего слагаемого с концом предыдущего. Вектор, соединяющий начало первого с концом последнего является суммой рассматриваемых векторов. 

Сумму двух векторов можно построить по правилу параллелограмма.  Для этого совмещают начало второго вектора с началом первого. Вектор, служащий диагональю параллелограмма, построенного на этих векторах, и исходящий из общего начала и будет суммой двух векторов (рис. 3. 7в).

 Разностью векторов называется такой вектор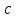, что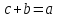,  (рис.3.8), разность векторовобозначается.

 Произведением вектора a на вещественное число  называется вектор, определяемый следующими условиями:

2) вектор  b коллинеарен вектору  a,

3) векторы  направлены одинаково, еслии противоположно, если. (Если, то).

Рис.3.8. Разность векторов.

Произведение вектора  на числообозначается.

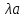Сложение векторов и умножение вектора на число обладают свойствами, указанными в 2.8.

Вектор, модуль которого равен единице, называется  единичным вектором или ортом.  Чтобы из неравного нулю вектора  a  получить орт коллинеарный  a, надо умножить вектор  на. Орт, коллинеарный, будем обозначать.

 Линейной комбинацией  векторов  …,называется выражение

,

где -  некоторые вещественные числа, которые называютсякоэффициентами линейной комбинации.

Теорема 3.1.  Пусть даны два неколлинеарных вектора  и. Любой компланарный с ними векторявляется их линейной комбинацией:. И такое представление единственно.

Теорема 3.2. Пусть даны три некомпланарных вектора ,и. Любой векторпредставляется, и при том единственным образом, в виде их линейной комбинации:

.

Векторы называютсялинейно зависимыми,  если существуют такие коэффициенты  , 0 одновременно не равные нулю, что

.

Если же из того, что линейная комбинация векторов равна нулю, следует, что все ее коэффициенты равны нулю, то векторы называются  линейно независимыми.

 Система линейно независимых векторов называется базисом  пространства, если любой вектор может быть представлен как их линейная комбинация.  В 2.8 мы выяснили, что такая система должна быть максимальной и что в n-мерном векторном пространстве любая максимальная система содержит точно n векторов. Таким образом, базис на плоскости состоит из двух векторов, в пространстве - из трех.

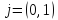Очевидно, что векторы илинейно независимые,  они образуют базис на плоскости, который называется декартовым. Аналогично векторыобразуют декартов базис в пространстве.

Пусть  - произвольный вектор трехмерного пространства, его можно разложить по декартовому базису, то есть представить в виде . По теореме 3.2. такое разложение единственно. Коэффициенты этого разложения называютсякоординатами вектора

Используя координаты вектора будем писать:

.

Как уже отмечалось, векторы мы будем обозначать буквами, написанными курсивом, координаты вектора будем обозначать теми же буквами, но написанными обычным шрифтом.

Теорема 3.3. Если известно разложение векторов по осям координат, то линейные операции над векторами можно заменить арифметическими операциями над координатами.

Пусть   и . Тогда

,   (3.5)

т.е., чтобы сложить два вектора, надо сложить их соответствующие координаты; чтобы умножить вектор на число, надо каждую его координату умножить на это число.

Векторы 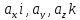называются составляющими векторапо координатным осям.

Рассмотрим две точки с координатами () ив декартовой системе координат. Поставим задачу найти координаты векторачерез координаты точек. Очевидно, что(рис.3.9).

Из (3.5) следует, что имеет координаты

.

То есть доказано следующее: чтобы найти координаты вектора, нужно из координат его конца вычесть координаты его начала.

Проекцией вектора на ось(называется длина отрезкамежду основаниями перпендикуляров, опущенных из точекна ось (рис.3.10), взятая со знаком плюс или минус в зависимости от того, совпадает ли направлениес направлением оси или противоположно ему. Проекция вектора на ось - скалярная величина, она равна длине (модулю) вектора, умноженной на косинус угла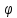между вектором и осью (рис.3.11):

, иначе ,

где и- координаты проекций точек

Проекция суммы векторовна какую-либо ось равна сумме проекций слагаемых векторов на ту же ось:

Из предыдущего следует, что если оси декартовой системы координат обозначить x, y, z, то

,

, (3.7)

Длина вектора (модуль) - это длина порождающего его отрезка, она вычисляется по формуле:

.2

Эти формулы выражают расстояние между двумя точками или длину диагонали прямоугольного параллелепипеда (рис 3.12).

Рис.3.12. Выражение длины вектора через его координаты

Направление вектора определяется углами, которые он образует с осями Ox, Oy, 0z. Эти углы называются направляющими (их обозначают соответственно ), а их косинусы -направляющими косинусами.

Они вычисляются по формулам:

(3.8)

Из (3.8) получаем тождество: +, которое часто используется для проверки правильности найденных значений направляющих косинусов.

Очевидно, что направляющие косинусы вектора являются координатами его орта   , т.е. .

Пример 3.2. Даны две координаты вектора  :Определить его третью координату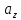при условии, что.

Имеем: т.е.=13. Тогда , т.е. .

Пример 3.3.  Вектор  составляет с координатными осями Ox и Oy углыи. Вычислить его координаты при условии, что

Имеем:

Из (3.6) имеем: аналогично

Пример 3.4. Даны два вектора  и. Определить проекции на координатные оси вектора.

Имеем: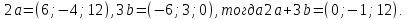 

Пример 3.5. Определить при каких значениях 

По условию коллинеарности , следовательно,.

Пример 3.6. Найти орт вектора  .

Имеем  , откуда  

Пример 3.7. Даны три вектора  . Разложить вектор.

Имеем:

 

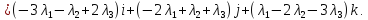
С другой стороны,  0. Значит

, ,

решая эту систему уравнений, найдем, что  ,,1, откуда

Отметим, что этот пример иллюстрирует последние формулы из предыдущего параграфа.

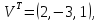
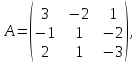
тогда и